kashiの日記

検索条件

タグで絞り込みその他(2)

日付で絞り込み 2013年(7) 2014年(31) 2015年(22) 2016年(17) 2017年(6) 2018年(7) 2019年(2) 2020年(1) 2021年(6) 2022年(3) 2024年(1)

全103件 (3/21ページ) 一覧表示に切り替え記事本文を表示

2020/02/12(水)kv-0.4.50

kvライブラリを0.4.50にアップデートしました。

今回は、卒論修論のシーズンが終わって、学生たちがライブラリを使うことで発見してくれた問題点の解決が主な内容です。利用して下さり、問題点を見つけてくれた学生のみなさまに感謝します。

内容は、

dd (double-double)用のfrexpが、入力が2のベキ乗よりも僅かに小さい値のときに正しく動作していなかったバグの修正。
interval.hppで、内部型としてfrexpが誤差を含む可能性があるような型を用いていたとき (例えばdd)、logがごく稀に正しい値を返していなかったバグの修正。
ddの(精度保証付きでない)sinとcosで、引き戻し処理が雑だったのを修正。

の3点です。特に、2番目は精度保証が破れている可能性があるため、重大な修正です。

interval<dd>のlogのバグ

前のddのfrexp問題に対処しているうちに、ある問題点に気付きました。それは、例えばx = 1+2^-1074みたいな上位と下位の数が非常に離れたdd数に対して、誤差無しでfrexpを実行することが不可能であるという問題です。このxに対するfrexpは、

y = 0.5+2^-1075
i = 1

となるべきですが、2^-1075を今のdoubleで表現することは出来ません。よって、必然的に誤差が生じることになります。

frexpなんてあまり使わないし、誤差が生じることを断っておけばいいか、くらいに思ったのですが、ライブラリ内でfrexpを使っている箇所を探していたらありました、数学関数logです。log(x)を計算するのに、x=y×2ⁱのように分解する方法を使っていました。そして、frexpに誤差が発生する可能性を考慮しておらず、frexpの戻り値を信用してそのまま計算していました。実際、doubleやmpfrではfrexpで誤差が発生することは無いのですが、ddだとこれが問題になります。

実際、log(1+2^-1074)をinterval<dd>で計算すると、

[0,0]

のように誤った(真値を含まない)値が計算されました。frexpは、返却値のうち仮数部yが問題であり、指数部iは信頼できるので、指数部iのみ使って、yは改めて区間演算するように精度保証付きlogの計算方法を改めることで対処しました。これで、

[0,9.881312916824930883531375857364427447301196052286495288511713650013510145404
17503730599672723271984759593129390891435461853313420711879592797549592021563756
25260142638062280905569163433569796420737743727211399746144610001277481830712996
87746249467945463392302800634307707961482524771311823420533171133735363740791206
21249863890543182984910658610913088802254960259419999083863978818160833126649049
51429573802945356031871047722310026960705298694403875805362142149834066644536895
06671441664863872184765786916736120212023012339619506156684554636658495809965049
46155275185449574931216955640746893939906729403594535543517025132110239826300978
22029020757254763345019116747794671979873296198823284114052741805584855350891304
5817507736501283943653106689453125e-324]

のように正しい値を含む区間が返されるようになりました。

一応表現可能とはいえ、1+2^-1074のような上位と下位が大きく離れたdd数が生成されることは稀であり、このバグに遭遇する確率は極めて低そうですが、可能性がゼロでない限り精度保証付き数値計算のライブラリとしては大きな問題と言えます。発見できて幸運でした。

ddのsin,cosの引き戻し問題

こちらは、精度保証付きのsin,cosでなく、sin,cosにintervalでない素のddを入れたときの問題です。元々ddに数学関数は実装されていなかったのですが、近似計算とはいえあれば便利だろうと、後で割と雑に実装したものです。が、sin,cosの引数を0近辺に引き戻すのに、2πを何度も引き算するようなあまりに雑な実装になっていました。多分後で直そうとして忘れていたものと思われます。元々精度保証は何も考えていない部分ですが、これだと大きな引数のときに計算時間が問題になりそうです。ちゃんと割り算するように直しました。

おわりに

ddは本当に鬼門で、何度も予想もしないバグに遭遇します。

精度保証付き数値計算のライブラリは、バグがあれば当然精度保証にならないわけで、プログラムにバグがないことをどうやって保証するのか、という宿命的な問題を抱えています。数学の定理の自動証明や、プログラムの自動検証を行うような研究もなされています。

(将来は分かりませんが)現在のところ、数学の定理が正しいかどうかは、多くの数学者が証明を検証してどうやら正しそうだ、と思えたら正しい、という段階のようです。プログラムも同じことで、大勢の人が使い、またソースコードを見て、どうやら正しそうだと思えたら正しい、とするしかないように思います。そのために、精度保証付き数値計算のプログラムは必ずオープンでなければならないし、また大勢の人に使われなければならないと考えています。

コメント（1件）

2019/11/21(木)kv-0.4.49

精度保証

久しぶりに、kvライブラリを0.4.49にアップデートしました。

今回は、以前から溜めていた、

辺に特異性を持つ2変数関数の二重積分
一点に特異性を持つ2変数関数の二重積分

を精度保証付きで行う機能を追加しました。

言葉で書くと簡単そうですが苦労しています。数値積分のページの第5,6節とか、辺及び一点にベキ型特異性を持つ2変数関数の二重積分を見て下さい。

コメント（0件）

2019/04/10(水)kv-0.4.48

精度保証

kvライブラリを0.4.48にアップデートしました。

今回は、区間演算の非常に基本的な部分の更新を含んでいます。

kvライブラリの区間演算は、端点に無限大を含む、 [0,\infty]のような半無限区間や、 [-\infty,\infty]のような無限区間を表現することが出来るように設計されています。これらは、区間が無限大という数?を含むという意味ではなく、 [0,\infty]ならば 0 \le x < \inftyのような、 [-\infty,\infty]なら -\infty < x < \inftyのような範囲を意味します。

このように端点に \inftyを許す区間演算を実装する場合、特に乗算で 0 \times \inftyに注意する必要があります。この計算はIEEE 754 Std.ではNaNになることになっていますが、区間演算の結果としてNaNはふさわしくありません。加算、減算、除算では適切に場合分けを行っていればNaNの危険はありませんが、乗算だけはきちんと考慮する必要があります。で、0.4.47以前では、片方が [0,0]でもう片方が無限大を含む区間だった場合の乗算で、何を考えていたのか、

\begin{eqnarray*} [0,0] \times [-\infty,\infty] &=& [-\infty, \infty] \\ [0,0] \times [c,\infty] &=& [-\infty, \infty] \\ [0,0] \times [-\infty,c] &=& [-\infty, \infty] \\ \end{eqnarray*}

のような計算をしていました。これらは、無限大を含む区間の意味を考えれば、当然 [0,0]になるべきものです。今回の0.4.48でこれを修正しました。福井大学の石井大輔先生のご指摘によります。大変ありがとうございました。

また、使ってる人がいるかどうか分からない、C++で気軽にリアルタイムグラフ表示 (matplotlib.hpp)の記事で書いたmatplotlib.hppですが、長方形を描画する関数rectにバグがあって正しい位置に描画されていなかったのを直しました。

コメント（0件）

2018/12/26(水)三部会連携応用数理セミナー

精度保証

応用数理学会の、三部会連携応用数理セミナーで講演してきました。年末恒例のセミナーですが、9月に行った「精度保証付き数値計算の基礎」チュートリアルの続編という意味合いもあります。9月の第4章のチュートリアルに続いて、第7章のチュートリアルでした。

そこでつかったスライドを上げておきます。

40分では少し駆け足になってしまったのが反省点。また、Affine Arithmeticは常微分方程式の精度保証でかなり重要な役割を果たしているにもかかわらず、教科書のどこにも説明がないのが大きな問題点だなあと感じました。

コメント（0件）

2018/12/09(日)Intlab 11の精度保証付きODE Solver

精度保証

Intlabは、Rump先生が開発しているMATLAB上で動く精度保証付き数値計算のためのソフトウェアです。残念なことに有償です(最近60ユーロに値上がりしました)。MATLABも有償なので何ともお金のかかる組み合わせですが、さまざまな面白いパッケージが入っています。最近(2018年9月)にバージョン11になりました。その目玉は、Florian Bünger先生の手による2つの精度保証付きODE Solverです。

一つは、先ごろ紹介したLohnerのAWAを移植したAWA Toolboxです。AWAはPascal-XSCというマイナーな言語で書かれていますから、メジャーなMATLABで書かれていた方がありがたい、という人もいるでしょう。

もう一つは、Berz, Makinoによる精度保証付き初期値問題ソルバーCOSY INFINITYを移植した Taylor model toolbox です。解を初期値に関して高次に展開することによる非常に高性能な精度保証付きアルゴリズムとして知られています。

今回は、この両者を実際に動かしてみたレポートです。MATLABはLinux上でR2018aを使いました。

まずはIntlab 11を買います。PayPalで支払うと、メールで6時間有効なダウンロードリンクが送られてくるので、INTLAB.zipをダウンロードしておきましょう。中身のファイルそのものは特にプロテクトがかかっているわけではなく自由に使えます。Intlabのインストールは簡単で、zipを解凍して好きなディレクトリに置くだけです。Intlabの機能を使う前に、MATLABでそのディレクトリにcdして startintlab とタイプします。初回はいろいろ調査するため時間がかかります。注意点は、IntlabはMATLABとoctave(MATLAB互換フリーソフト)に対応していますが、残念ながら精度保証付き初期値問題のためのAWA toolboxとTaylor model toolboxはoctaveに対応していません。octaveでのテストを行わずに開発していたそうで、またいくつかのoctaveの非互換の部分が問題ですぐに対応するのは難しいそうです。

次に実際に動かしてみます。例題は、以前LohnerのAWAを紹介した記事と同じ、van der Pol方程式:

\begin{align*} \frac{dx}{dt} &= y \\ \frac{dy}{dt} &= \mu (1-x^2)y - x \end{align*}

で、\mu=1とし、初期値 (x(0),y(0))=(1,1)でt\in[0,20]の範囲で計算する問題にしました。

AWA toolbox

まずAWA toolboxの方の使い方を説明します。詳細はDEMOAWA Short demonstration of the AWA toolboxのページを見て下さい。

最小限のコードはこんな感じだと思います。これを適当な名前 (例えばhoge.m) でファイルを作成し、MATLAB上でhogeで実行できます。

init = [1; 1];
[T,X] = awa(@vdp, @vdp_J,  [0, 20], init);
format long e
awa_disp(T,X);

function f = vdp(t, x)
        mu = 1;
        f =     [x(2);
                mu*(1-x(1)^2)*x(2)-x(1)];
end

function J = vdp_J(t, x)
        mu = 1;
        J =     [typeadjust(0, x), typeadjust(1, x);
                -2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end

このように、ODEの右辺を定義する関数(ここではvdp)と、そのヤコビ行列を返す関数(ここではvdp_J)を定義し、関数awaを呼びます。awaの計算したデータを分かりやすく表示してくれるのがawa_dispです。ヤコビ行列を定義するのが面倒ですし、Intlabの持っている自動微分機能でなんとかなりそうな気がするのですが、高速化のためにやむを得なかったそうです。typeadjustという関数が使われていますが、関数の戻り値に定数があるときはこうやって型を補正する必要があります。

更に、関数awaの第5引数に

awaset('order',10,'h0',0,'EvalMeth',4,'AbsTol',1e-16,'RelTol',1e-16)

のような関数を使って、様々なパラメータを変更することができます(これらの値はデフォルト値)。変更したいパラメータの名前を奇数番目の引数に、値を偶数番目の引数に書きます。これを使って、LohnerのAWAを紹介した記事に合わせてTaylor展開の次数を24次にした、

init = [1; 1];
tic; [T,X] = awa(@vdp, @vdp_J,  [0, 20], init, awaset('order', 24)); toc
format long e
awa_disp(T,X);

function f = vdp(t, x)
        mu = 1;
        f =     [x(2);
                mu*(1-x(1)^2)*x(2)-x(1)];
end

function J = vdp_J(t, x)
        mu = 1;
        J =     [typeadjust(0, x), typeadjust(1, x);
                -2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end

を実行してみました。すると、次のような解が得られました。

経過時間は 20.973900 秒です。
t = 0
    [y_1] = [  1.000000000000000e+000,  1.000000000000000e+000]    d([y_1]) = 0.00e+00
    [y_2] = [  1.000000000000000e+000,  1.000000000000000e+000]    d([y_2]) = 0.00e+00
 
t = 1.911224186649680e-01
    [y_1] = [  1.169708666105268e+000,  1.169708666105269e+000]    d([y_1]) = 6.66e-16
    [y_2] = [  7.615010659752849e-001,  7.615010659752856e-001]    d([y_2]) = 4.44e-16

(中略)

t = 1.992657858092985e+01
    [y_1] = [  2.000739935214436e+000,  2.000739935214461e+000]    d([y_1]) = 2.31e-14
    [y_2] = [  1.939352117515359e-001,  1.939352117517785e-001]    d([y_2]) = 2.42e-13
 
t = 20
    [y_1] = [  2.008487917798417e+000,  2.008487917798427e+000]    d([y_1]) = 7.99e-15
    [y_2] = [  2.328985430648321e-002,  2.328985430667890e-002]    d([y_2]) = 1.96e-13

オリジナルのAWAのt=20における解は、

t =  2.000000000000000E+001
[ 2.00848791779841E+000, 2.00848791779843E+000]  8.00E-015  4.0E-015
[ 2.32898543064796E-002, 2.32898543066811E-002]  2.02E-013  8.7E-012

でした。どちらも精度保証付きソルバーなので、両者の共通部分に真の解があることになります。計算時間はオリジナルが0.81secだったのに対してこちらは20.97secと、かなり遅くなってしまっています。Bünger先生によるとかなり高速化の工夫をしたとのことですが、これがMATLABの限界でしょうか。

Taylor model toolbox

こちらの最小限のコードはこんな感じだと思います。詳細はDEMOTAYLORMODEL Short demonstration of the Taylor model toolboxを見て下さい。

init = [1; 1];
[T,X,Xr] = verifyode(@vdp, [0, 20], init);
format long e
verifyode_disp(T,X,Xr,init);

function f = vdp(t, x, i)
        mu = 1;
        if nargin == 2 || isempty(i)
                f =     [x(2);
                        mu*(1-x(1)^2)*x(2)-x(1)];
        else
                switch i
                case 1
                        f =     x(2);
                case 2
                        f = mu*(1-x(1)^2)*x(2)-x(1);
                end
        end
end

こちらはawaの方にあったヤコビ行列を書く必要はありません。その代わり、右辺を定義する関数にt, xに続く第3の変数が増えており、そこに自然数が与えられたらその番号に対応する右辺の式だけを計算して返すことが要求されています。これも高速化のためです。関数verifyodeで計算した値をverifyode_dispで表示するのはAWA toolboxと同じですが、渡す変数の数がT, X, Xrと3つに増えており、またverifyode_dispには初期値も渡す必要があります。

AWA toolboxと同様に

verifyodeset('order',12, 'h0',0,'loc_err_tol',1e-10,'shrinkwrap',1,'precondition',0,'blunting',0)

のようなオプションを第4引数に指定することによって動作をカスタマイズできます。AWAと違って非常にオプションが多く、またオプションの指定によって大きく性能が違うようなので、まずどんなオプションがいいか調べてみました。方程式は同じvan der Polでt=15まで計算、orderは18に固定して、区間幅の変化を調べてみました。それを行った結果が次のグラフです。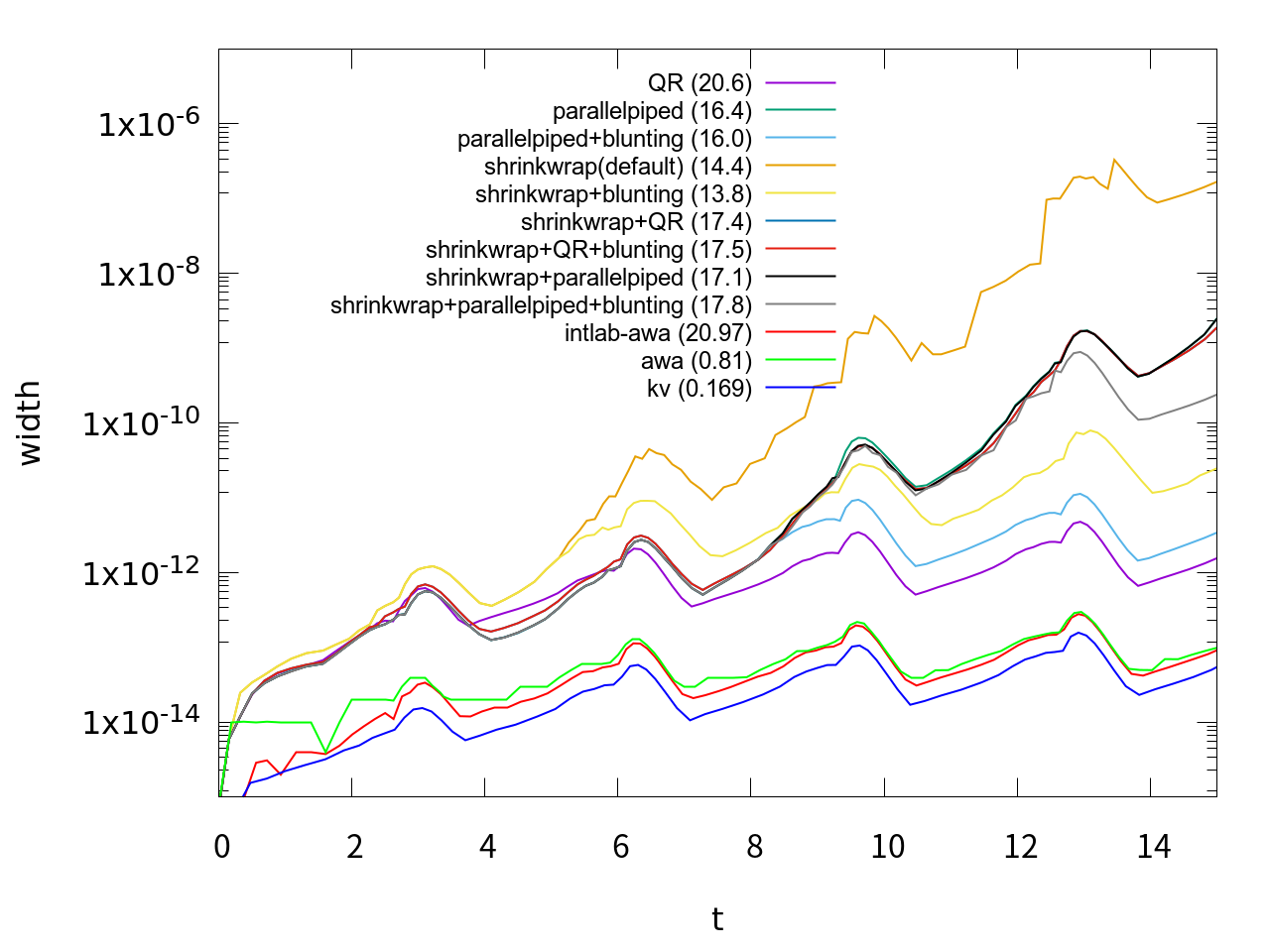

グラフの説明の上から9つが今回のTaylor Model Toolboxの計算結果で、下3つは他のもの(参考値)です。カッコ内の数値は計算時間(秒)です。グラフの説明は、それぞれ次のようなオプションと対応しています。横軸がt、縦軸は計算結果の区間幅を表しています。

	shrinkwrap	precondition	blunting
QR	0	1	0
parallelpiped	0	2	0
parallelpiped + blunting	0	2	1
shrinkwrap(default)	1	0	0
shrinkwrap + blunting	1	0	1
shrinkwrap + QR	1	1	0
shrinkwrap + QR + blunting	1	1	1
shrinkwrap + parallelpiped	1	2	0
shrinkwrap + parallelpiped + blunting	1	2	1

これを見ると、デフォルトの1,0,0 (shrinkwrapのみ) が一番悪く、0,1,0 (QRのみ)が一番いいことが分かります。なぜこれがデフォルト値なのか理解に苦しみますが。

このパラメータを使い、更に次数を24に、loc_err_tolは1e-10に (いろいろ試すとこの数値が良かった) 設定して、以下を実行してみました。

init = [1; 1];
tic; [T,X,Xr] = verifyode(@vdp, [0, 20], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);

function f = vdp(t, x, i)
        mu = 1;
        if nargin == 2 || isempty(i)
                f =     [x(2);
                        mu*(1-x(1)^2)*x(2)-x(1)];
        else
                switch i
                case 1
                        f =     x(2);
                case 2
                        f = mu*(1-x(1)^2)*x(2)-x(1);
                end
        end
end

すると、次のような解が得られました。

経過時間は 24.897000 秒です。
t = 0
    [y_1] = [  1.000000000000000e+000,  1.000000000000000e+000]    d([y_1]) = 0.00e+00
    [y_2] = [  1.000000000000000e+000,  1.000000000000000e+000]    d([y_2]) = 0.00e+00
 
t = 2.218563039351837e-01
    [y_1] = [  1.192420354444434e+000,  1.192420354444441e+000]    d([y_1]) = 5.77e-15
    [y_2] = [  7.162286750812696e-001,  7.162286750812727e-001]    d([y_2]) = 2.89e-15

(中略)

t = 1.986588757581453e+01
    [y_1] = [  1.983929113336597e+000,  1.983929113337129e+000]    d([y_1]) = 5.31e-13
    [y_2] = [  3.648228353937841e-001,  3.648228353977482e-001]    d([y_2]) = 3.96e-12
 
t = 20
    [y_1] = [  2.008487917798372e+000,  2.008487917798472e+000]    d([y_1]) = 9.95e-14
    [y_2] = [  2.328985430522710e-002,  2.328985430793645e-002]    d([y_2]) = 2.71e-12

少し精度が落ちているものの、同様に精度保証された解が得られました。計算時間は25秒弱とやや遅めです。

Taylor model toolboxに指定した

verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)

は試行錯誤の結果ですが、もっと良い設定があるかもしれません。情報は募集中です。当然、方程式や初期値が違えばまた最適値も変わる可能性が高いです。Taylor modelは前評判からするとやや性能が出ておらず、少しがっかりしています。

二重振り子の精度保証付き数値計算で勝負

最後に、二重振り子の精度保証付き数値計算の記事の二重振り子の軌道を計算させてみて、AWA, kvライブラリと比較してみました。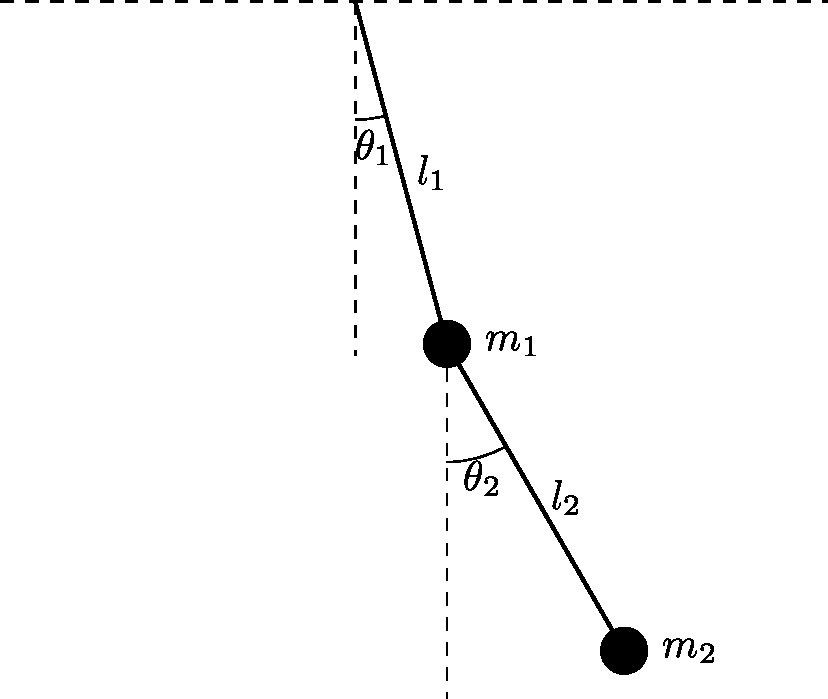

使った式は、以前と同じ

\begin{align*} & (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2) + m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2) +(m_1+m_2)g \sin \theta_1= 0 \\ & l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2} -l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0 \end{align*}

\begin{align*} m_1 &= m_2 = 1 \\ l_1 &= l_2 = 1 \\ g &= 9.8 \\ \end{align*}

\begin{align*} \theta_1(0) &= \frac{3}{4}\pi \\ \theta_2(0) &= \frac{3}{4}\pi \\ \dot{\theta_1}(0) &= 0 \\ \dot{\theta_2}(0) &= 0 \end{align*}

です。使用したプログラムは、Taylor model toolboxが、

init = [intval('pi')*0.75; intval('pi')*0.75; 0; 0];
tic; [T,X,Xr] = verifyode(@doublependulum, [0, 11], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);

function f = doublependulum(t, x, i)
	persistent g;
	if (isempty(g))
		g = intval('9.8');
	end
	m1 = 1;
	m2 = 1;
	l1 = 1;
	l2 = 1;
	t1 = cos(x(1) - x(2));
	t2 = sin(x(1) - x(2));
	a = (m1 + m2) * l1;
	b = m2 * l2 * t1;
	c = l1 * l2 * t1;
	d = l2 * l2;
	dt = a*d - b*c;
	v1 = -m2 * l2 * x(4) * x(4) * t2 - (m1 + m2) * g * sin(x(1));
	v2 = l1  * l2 * x(3) * x(3) * t2 - g * l2 * sin(x(2));
	if nargin == 2 || isempty(i)
		f = 	[x(3);
			x(4);
			(d * v1 - b * v2) / dt;
			(-c * v1 + a * v2) / dt];
	else
		switch i
		case 1
			f = 	x(3);
		case 2
			f = 	x(4);
		case 3
			f = (d * v1 - b * v2) / dt;
		case 4
			f = (-c * v1 + a * v2) / dt;
		end
	end
end

AWAが、

M1 = 1
M2 = 1
L1 = 1
L2 = 1
G = 9.8

T1 = cos(U1 - U2)
T2 = sin(U1 - U2)
A = (M1 + M2) * L1
B = M2 * L2 * T1
C = L1 * L2 * T1
D = L2 * L2
DT = A*D - B*C

V1 = -M2 * L2 * U4 * U4 * T2 - (M1 + M2) * G * sin(U1)
V2 = L1 * L2 * U3 * U3 * T2 - G * L2 * sin(U2)

F1 = U3
F2 = U4
F3 = ( D*V1 - B*V2) / DT
F4 = (-C*V1 + A*V2) / DT

;;

1 0 13 0 24

4 0

[2.35619449019234492884698253745961,2.356194490192344928846982537459636] [2.35619449019234492884698253745961,2.356194490192344928846982537459636] 0 0
n

1e-16 1e-16

kvが、

#include <iostream>
#include <limits>
#include <kv/ode-maffine.hpp>
#include <kv/constants.hpp>
#include <kv/ode-callback.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;


struct DoublePendulum {
	template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
		ub::vector<T> y(4);
		ub::matrix<T> tm(2,2);
		ub::vector<T> tv(2);

		T a, b, c, d, t1, t2;

		static const T m1 = T(1.);
		static const T m2 = T(1.);
		static const T l1 = T(1.);
		static const T l2 = T(1.);
		static const T g = kv::constants<T>::str("9.8");

		t1 = cos(x(0) - x(1));
		t2 = sin(x(0) - x(1));

		a = (m1 + m2) * l1;
		b = m2 * l2 * t1;
		c = l1 * l2 * t1;
		d = l2 * l2;

		tm(0,0) = d;
		tm(0,1) = -b;
		tm(1,0) = -c;
		tm(1,1) = a;
		tm /= (a*d - b*c);

		tv(0) = -m2 * l2 * x(3) * x(3) * t2 - (m1 + m2) * g * sin(x(0));
		tv(1) = l1 * l2 * x(2) * x(2) * t2 - g * l2 * sin(x(1));

		tv = prod(tm, tv);

		y(0) = x(2);
		y(1) = x(3);
		y(2) = tv(0);
		y(3) = tv(1);

		return y;
	}
};

int main()
{
	ub::vector<itv> ix;
	itv end;
	std::cout.precision(17);

	ix.resize(4);
	ix(0) = 0.75 * kv::constants<itv>::pi();
	ix(1) = 0.75 * kv::constants<itv>::pi();
	ix(2) = 0.;
	ix(3) = 0.;

	// end = std::numeric_limits<double>::infinity();
	end = 17.05;
	kv::odelong_maffine(DoublePendulum(), ix, itv(0.), end, kv::ode_param<itv::base_type>().set_verbose(1));
}

です。IntlabのAWA toolboxは、関数のヤコビ行列を書くのが面倒で試しませんでした。

計算結果を図示します。

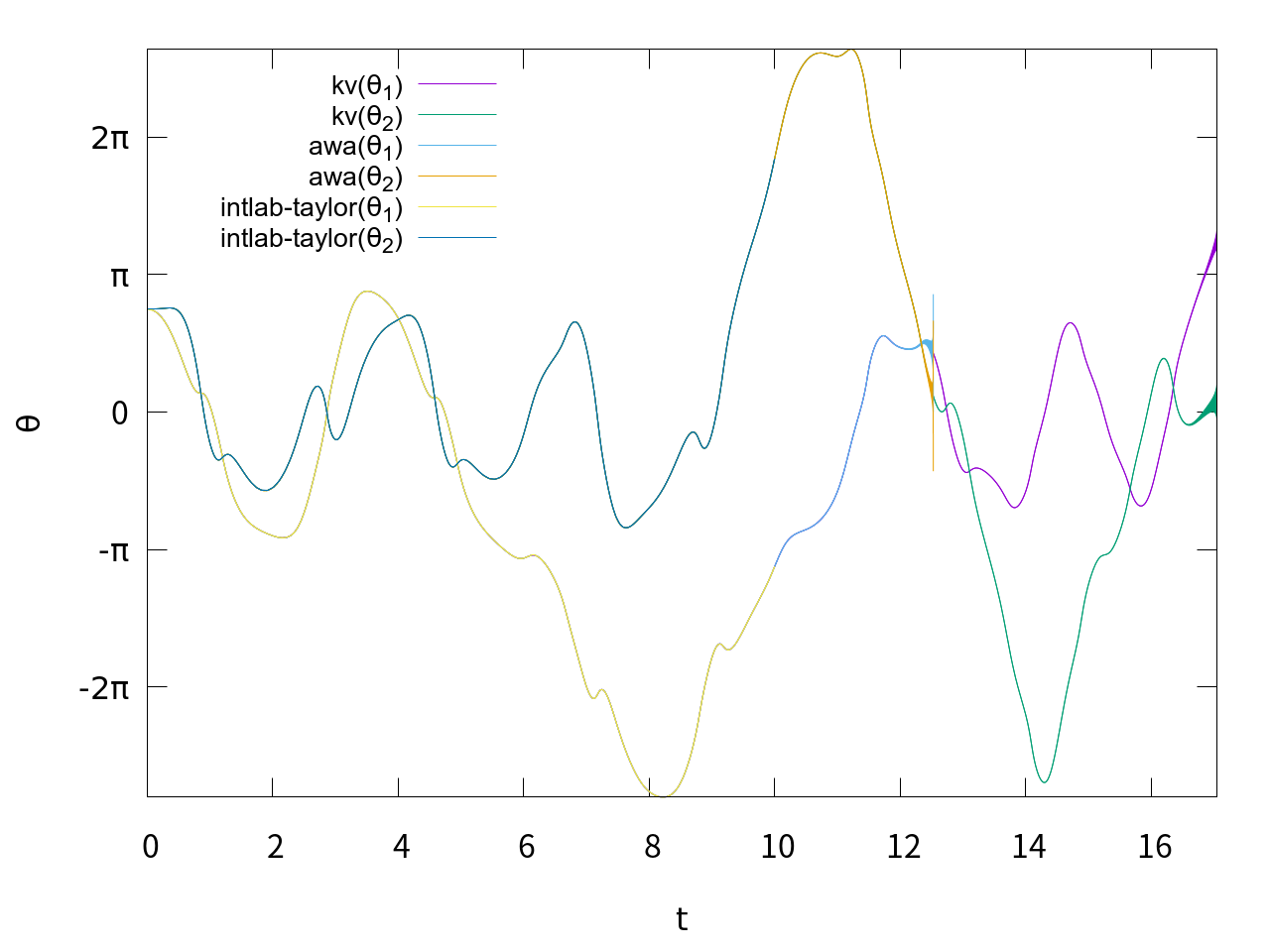
このようになりました。さすがは精度保証付きソルバー、当たり前ではありますがグラフがぴったり重なっています。Taylor model toolboxはt=10までは計算できましたが、t=11では計算が止まりませんでした。AWAはt=12過ぎで解が発散しました。kvはt=17過ぎまで計算できました。解の区間幅を図示すると、

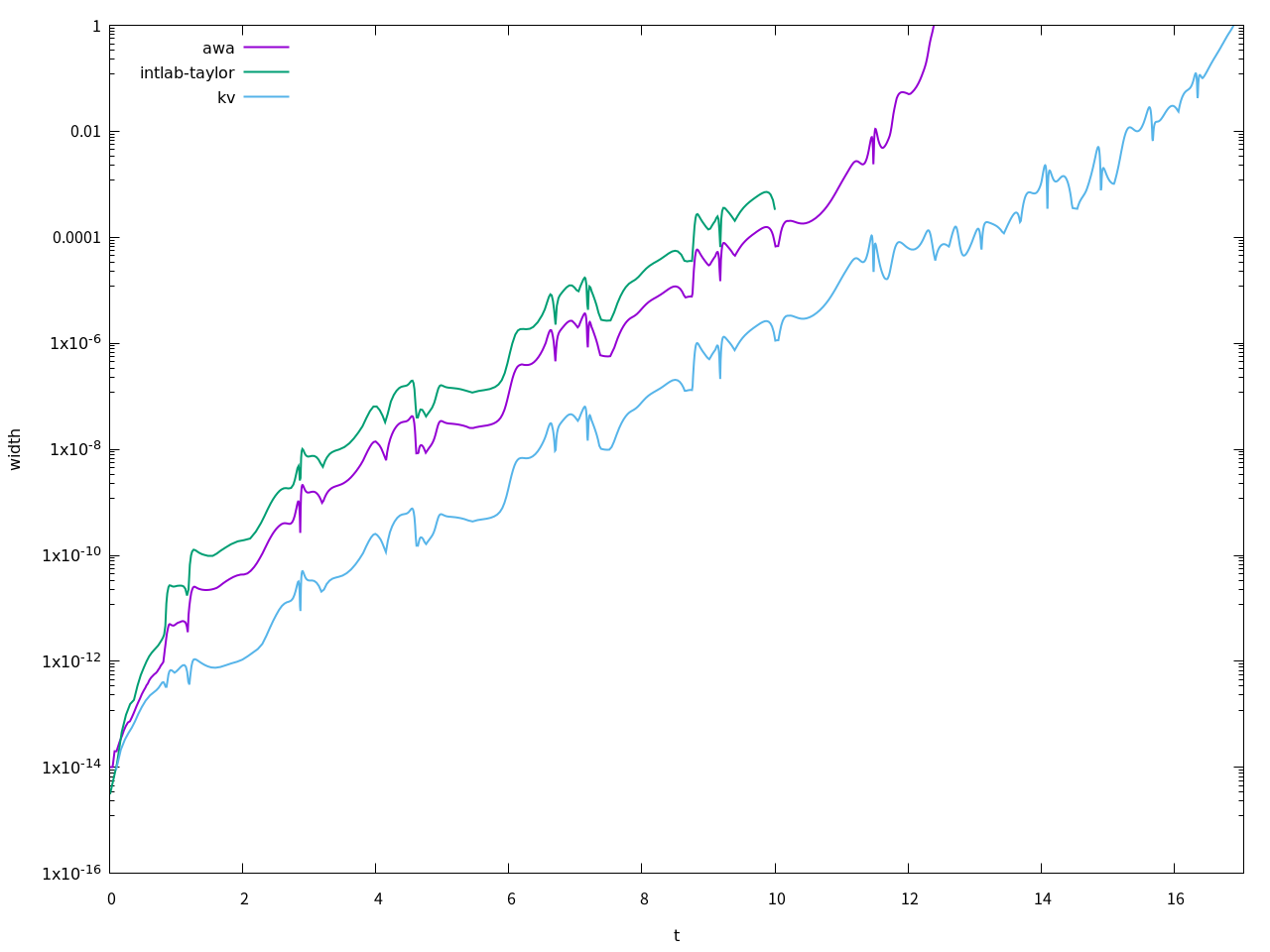
このようになりました。kvが長い時間区間幅が発散せずに持ちこたえていることが分かります。

計算時間は、全員が計算可能なt=10までで、Taylor model toolboxが5時間20分17秒、AWAが17.9秒、kvが22.9秒でした。

kvは、他の2つには不可能な、内部の演算型を全てdouble-double(疑似4倍精度)に変えて精度保証付き計算を行うこともでき、この場合は軽々とt=30以上まで計算することができます。~~まあ、kvの圧勝なわけですが、他のソルバーかかってこいや。~~もっと他の例題、特にstiffな例題や、他のソルバーを試してみたいと思います。

コメント（0件）