2018/11/29(木)kv-0.4.47
実は、日記には書きませんでしたが、昨日、kv-0.4.46にアップデートしています。
kv-0.4.46では、精度保証付きODE solverのstep sizeの制御部分が自分の意図通りに書かれていなかったいくつかのバグを修正しました。以前のversionでも精度保証が破れていることはないはずですが、step sizeの戦略が変わるので計算結果は0.4.45以前とは少し変わります。特にstiffな問題に関しては、大きく変わる可能性もあります。
kv-0.4.47もODE solverに関する変更です。ユーザから見れば、ode-maffine0.hppが削除されたこと以外はほとんど変わっていません。しかし、内部には大きな変更が入りました。kv-0.4.35で行った変分方程式の解き方の改善は、ode-maffineに対するものでしたが、それをode-autodifに直接組み込むようにしました。これにより、(ほとんど使われていないでしょうけど)ode-qrがstiff ODEに強くなっていることが予想されます。
変更が大きいので気分的にスナップショットを残しておきたくて、短期間でのversion upになりました。いろいろチェックはしたつもりですが、何か不具合がありましたらお知らせ下さい。
2018/11/24(土)LohnerのAWAで遊ぼう
古いソフトウェアなので手元で動かした経験のある人は少ないと思いますが、今回は、この知る人ぞ知るソフトウェアを手元で動かして、実際に初期値問題の精度保証を行うまでの方法を書きたいと思います。
AWAのホームページは AWAにありますが、ここには古い機種でのバイナリしかありません。awa.src.tar.Zはありますが、ここには拡張子.pのファイルしか入っていません。AWAは、精度保証付き数値計算のために開発されたPascal-XSCという言語で書かれています。よってAWAを使うには、まずPascal-XSCコンパイラを準備しなければなりません。幸いなことにPascal-XSCのパッケージはその中に丸ごとAWAを含んでいて、Pascal-XSCをmakeすればAWAが手に入ります。
Pascal-XSCは、XSC LanguagesのページにあるPascal-XSCの欄の、Free Download (Compiler and Toolbox)にあります。そこに、ソースコード ( p-xsc-3.6.2.tar.gz (released 2005-12-19) ) があるのでそれをダウンロードしましょう。
以下、makeの仕方を示します。Ubuntu 18.04 (64bit)で行いました。32bitのbinaryを作成するので、
sudo apt install build-essential sudo apt install gcc-multilibが必要だと思います(後者が重要)。archiveを展開するとMakefileがあり、まずMakefileを書き換えます。どういうわけだか単にmakeするだけでいわゆるmake installに相当する作業を行い更にpathまで切ろうとするというお行儀の悪さなので、少し手を入れます。まず、Makefileの最初の方の
PREFIX=/usr/local/p-xscの部分を書き換えて、書き込んでもよい場所を絶対パスで指定します。自分は念の為ホームディレクトリの中の適当な場所を指定しました。また、Makefile中の
@echo "****************************************************"
@echo " Install System PATH in /etc/profile.local as root *"
@echo " or in ~/.bashrc as user *"
@echo "****************************************************"
cd profile; ./uidtest.sh ${PREFIX}
の部分で/etc/profile.localというシステムファイルに書き込もうとするので、ここは#でコメントアウトしておきます。makeそのものは自分の環境では問題なく出来ました。PREFIXで指定した場所の bin/awa が目的のAWAのコンパイル済み実行ファイルです。Pascal-XSC言語を使うつもりがないならば、
- 生成されたawaの実行ファイル
- prts/rts/o_msg1.h (Pascal-XSCの"runtime message"。current dirに置く)
- awa/examples/* (AWAのサンプルファイル)
さて、実際に初期値問題を精度保証する方法を示します。例題は、van der Pol方程式を1階に直した
\begin{align*}
\frac{dx}{dt} &= y \\
\frac{dy}{dt} &= \mu (1-x^2)y - x
\end{align*}
を、\mu=1とし、初期値 (x(0),y(0))=(1,1)でt\in[0,20]の範囲で計算することにしました。まず、test.inを2 test.dat test.outの内容で作成します。「2」は方程式の次元、test.datは方程式を記述するファイル、test.outは出力するファイル名です。次に、test.datを、
F1 = U2 F2 = 1 * (1-U1*U1) * U2 - U1 ;; 1 0 20 0 24 4 0 1 1 1e-16 1e-16の内容で作成し、
awa < test.inとすると、test.outが生成されます。この場合は、
ode read from file test.dat
out = 1
T_start = 0.000000000000000E+000
T_end = 2.000000000000000E+001
initial stepsize h = 0.000000000000000E+000
order p = 24
enclosure method : intersection of interval-vector and QR-decomposition
output : function values
t = 0.000000000000000E+000
[ 1.00000000000000E+000, 1.00000000000000E+000] 0.00E+000 0.0E+000
[ 1.00000000000000E+000, 1.00000000000000E+000] 0.00E+000 0.0E+000
h = 1.911222934722900E-001
t = 1.911222934722900E-001
[ 1.16970857077089E+000, 1.16970857077090E+000] 6.67E-016 5.7E-016
[ 7.61501247518094E-001, 7.61501247518095E-001] 3.34E-016 4.4E-016
h = 1.831474304199219E-001
(中略)
t = 1.993603903055191E+001
[ 2.00246009621560E+000, 2.00246009621563E+000] 2.18E-014 1.1E-014
[ 1.69827498867334E-001, 1.69827498867578E-001] 2.43E-013 1.5E-012
h = 6.396096944808960E-002
t = 2.000000000000000E+001
[ 2.00848791779841E+000, 2.00848791779843E+000] 8.00E-015 4.0E-015
[ 2.32898543064796E-002, 2.32898543066811E-002] 2.02E-013 8.7E-012
Number of integration steps: 134
Time: 1.64 sec
のようなファイルが生成されました(計算速度はLet's Note RZ4で)。時刻毎のx,yの値が区間で表示されていますが、真の軌道がこの区間内にあることが数学的に厳密に保証されています。区間の後の2つの数値はそれぞれ区間幅、相対区間幅を表しているようです。x,yそれぞれの上限、下限をプロットしてみましたが、このくらいの簡単な問題だと差はグラフ上では見えません。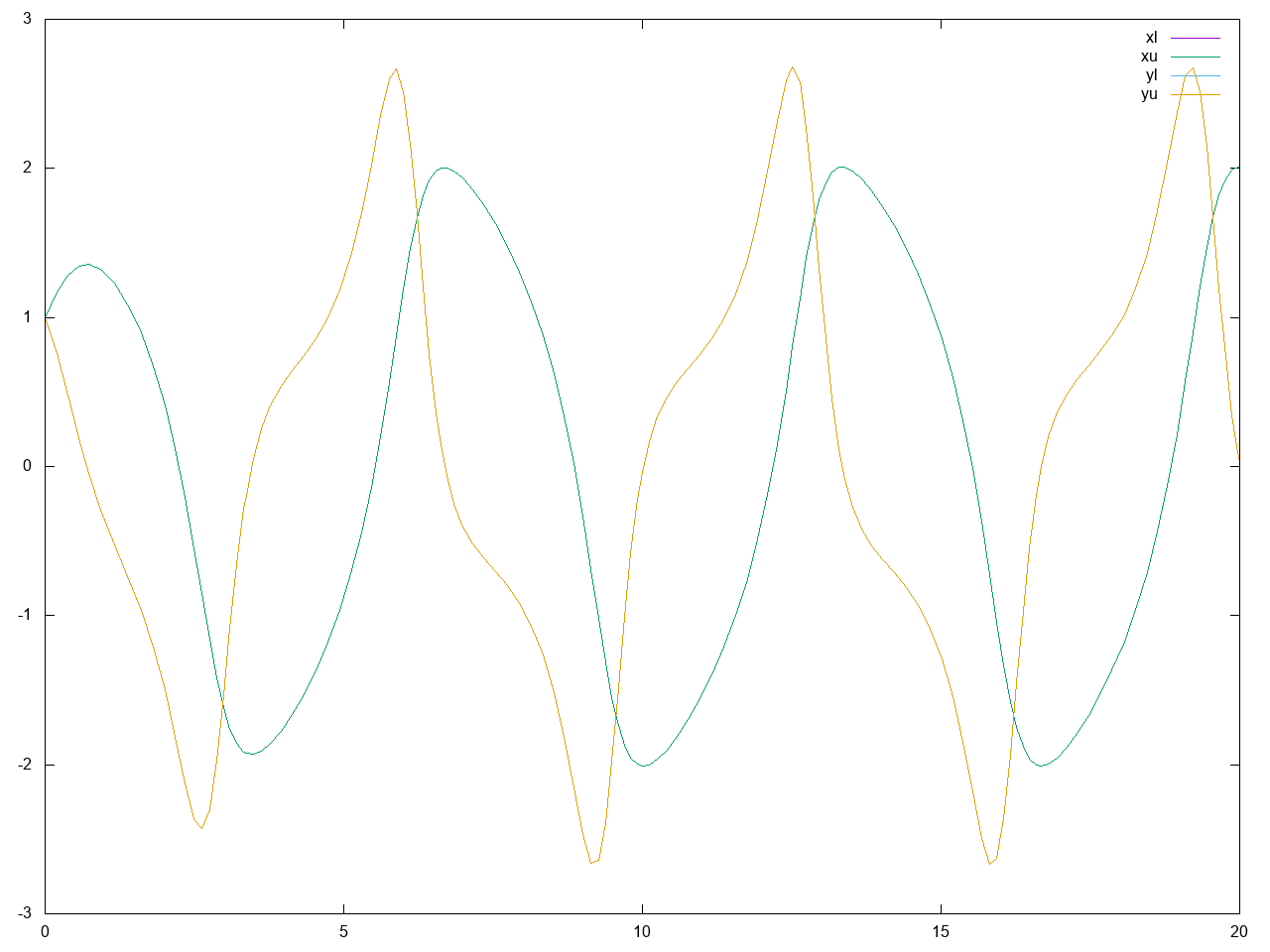
なお、途中は折れ線で繋いだだけなので、自動で分点に選ばれた134点以外の部分は精度保証されたグラフではありません。
方程式を記述するファイルの書き方を説明します。
F1 = U2 F2 = 1 * (1-U1*U1) * U2 - U1 ;;方程式の右辺を記述します。変数がU1, U2で、方程式がF1, F2です。次元の数だけ記述します。
1 0 20 0 24
- 1 : 1以外のnを指定すると、nステップ毎に表示するようになります。基本1でいいと思います。
- 0 20 : tの変域。0から20まで計算します。
- 0 : 初期ステップ幅。0なら自動推定してくれるので、基本0でいいと思います。
- 24 : 内部で使うTaylor展開の次数
4 0
- 4 : 内部で使うアルゴリズム。1から4までありますが、4が一番優秀です。
- 0 : 結果の表示の方法。0しか実装されていないっぽい。
1 1初期値です。ここだけ少し注意が必要です。まず、初期値には、[1,2] [1,1.5]みたいな区間を書くこともできます。また、1.1のようなIEEE754のdoubleで書けないような数が与えられると、自動的にそれを包含する区間として扱います。初期値のうちどれか一つでも区間になるような場合は、
1 1.1 nのように後に「n」を補わなければなりません。「j」でもいいのですが、相対誤差の表示に影響するだけで、計算そのものには影響しません。しかし、初期値が区間になる場合はnかjのどちらかを書く必要があります。
1e-16 1e-16それぞれ、1ステップ毎に許容される絶対誤差、相対誤差を表します。
極めて優秀なアルゴリズムとソフトウェアで、のちに初期値問題の精度保証の研究者はなかなかこれを超えられずに苦労することになります。優れた仕事に対する尊敬の念を込めて、この記事を書きました。
2018/11/18(日)kv-0.4.45
今回はあまり大きな変更はありません。
- 自動微分でpow(x,0)みたいな(あまり意味のない)記述があったときにエラーになっていたバグを直した。
- Krawczyk法での非線形方程式の精度保証で、1変数の場合のエラーハンドリングに問題があって精度保証失敗時に落ちていたバグの修正。
- DKA法の内部精度をdouble以外にするとコンパイルできなかったバグの修正。
2018/09/10(月)「精度保証付き数値計算の基礎」チュートリアル
精度保証付き数値計算の基礎
という本を出しました。私が執筆したのは、第4章「数学関数の精度保証」と、第7章「常微分方程式の精度保証付き数値解法」です。
で、今回、
「精度保証付き数値計算の基礎」チュートリアル
で話させていただきました。そこで使ったスライドを上げておきます。内容は第4章の数学関数の精度保証の話で、発表時間は20分だったので、簡単な内容です。割と多くの方に来ていただいてとても嬉しかったです。
なお、今回のチュートリアルは6章までで、7章のODEと8章のPDEについては年末に別の機会を準備中です。
2018/06/17(日)kv-0.4.44
変更点は、
- dd.hpp, rdd-hwround.hpp, rdd-nohwround.hppを修正し、主にddのオーバーフローに 関するバグを修正。
- affine.hppのepsilon_reduceで、与えられたaffineベクトルが1次元だった場合に正しく 動かないバグを修正。
- rkf78.hpp追加
- その他細かい修正
今回は、dd (double double) を使った区間演算に関する重大なバグフィックスを含んでいます。加減乗除の結果がオーバーフローするかしないかギリギリの値の場合の処理に問題があり、確率は低いものの、精度保証が正しく行われない可能性があるバグです。
以下、その詳細について説明します。ddでの区間演算は、例えば加算では真値と同じか真値よりも大きい値を計算するadd_up、真値と同じか真値よりも小さい値を計算するadd_downによって実現されています。例えばadd_downは、次のようなアルゴリズムによって実現されていました。簡単のため、python-likeに書いています。dd数(x1,x2)とdd数(y1,y2)の和を下向き丸めで計算するものです。
def dd_add_down(x1, x2, y1, y2) :
z1, z2 = twosum(x1, y1)
if z1 == -float("inf") :
return z1, 0
if z1 == float("inf") :
return sys.float_info.max, sys.float_info.max * 2.**(-54)
down()
z2 = z2 + x2 + y2
near()
z1, z2 = twosum(z1, z2)
return z1, z2
無誤差のtwosumはそのまま計算し、誤差の入る可能性のある「z2 + x2 + y2」の部分は下向き丸めで計算することで、下向き丸めの結果を得ています。これに加えて、赤字で示したオーバーフローの処理を行っています。ddライブラリではIEEE754と同様の無限大の取り扱いを出来るように設計しています。これは、端点に無限大を許す区間演算の実装には不可欠です。無限大は(inf,0)または(-inf,0)のような内部表現にしています。また、twosumは
def twosum(a, b) :
x = a + b
if (abs(a) > abs(b)):
tmp = x - a
y = b - tmp
else:
tmp = x - b
y = a - tmp
return x, y
のような実装になっていますが、a,bが無限大でなくa+bがオーバーフローした場合、(inf,-inf)を返すことが分かります。add_downのオーバーフロー処理は、- 負の方向へオーバフローした場合は、(-inf,0)を返す。
- 正の方向へオーバーフローした場合は、下向き丸めなので無限大を返すのは誤りで、ddで表現できる正の最大数を返す。
自分はこれで抜けは無いと安易に考えていたのですが、研究室の修士の学生だった宮崎敏文さんにまずい場合があるのではないかと指摘され、確かに問題があることが分かりました。
問題は3つあります。
- 最初の問題は、「add_downで正の方向にオーバーフローするとddでの正の最大数を返すが、x1+y1は確かにddの正の最大数より大きいが、x2とy2が負の数で、全体の合計はddの正の最大数を下回ることがあるのではないか」というものです。宮崎さんの指摘はこの問題でした。
- 二つ目の問題は、「最初のtwosumの後は無限大の処理をしているが、二つ目のtwosumの後は何もしていない。最初のtwosumではオーバーフローしないが、二つ目のtwosumでオーバーフローする可能性があるのでは」というものです。
- 三つ目の問題は、「add_downの引数の片方がinf、もう片方が非infだったとき、その和はinfになるべきだが、ddの正の最大数が返ってくる」というものです。
def dd_add_down(x1, x2, y1, y2) :
if abs(x1) == float("inf") or abs(y1) == float("inf") :
return x1 + y1, 0
z1, z2 = twosum(x1, y1)
if z1 == -float("inf") :
return z1, 0
if z1 == float("inf") :
z1 = sys.float_info.max
z2 = sys.float_info.max * 2.**(-54)
down()
z2 = z2 + x2 + y2
near()
z1, z2 = twosum(z1, z2)
if z1 == -float("inf") :
return z1, 0
if z1 == float("inf") :
z1 = sys.float_info.max
z2 = sys.float_info.max * 2.**(-54)
return z1, z2
すなわち、まず引数に無限大が含まれている場合を先に処理し(3.の対策)、次にtwosum後に正方向にオーバーフローして正の最大数に置き換えた場合はreturnせずにそのまま計算を継続するようにし(2.の対策)、最後に2回目のtwosumに対しても同じようにオーバーフロー処理を行なう(2.の対策)ようにしました。これによって、次のように問題が修正されました。
1.の問題は、例えば(x_1,x_2)=(2^{1023}-2^{970},-(2^{969}-2^{916})), (y_1,y_2)=(2^{1023},-2^{969})という入力で発生します。
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
int main()
{
std::cout.precision(32);
kv::interval<kv::dd> x, y, z;
x.lower().a1 = pow(2., 1023) - pow(2., 970);
x.lower().a2 = -(pow(2., 969) - pow(2., 916));
x.upper() = x.lower();
std::cout << x << "\n";
y.lower().a1 = pow(2., 1023);
y.lower().a2 = -pow(2., 969);
y.upper() = y.lower();
std::cout << y << "\n";
z = x + y;
std::cout << z << "\n";
}
これを改修前のkvで計算すると[8.9884656743115780417662938029053e+307,8.9884656743115780417662938029054e+307] [8.9884656743115790396864485702651e+307,8.9884656743115790396864485702652e+307] [1.797693134862315807937289714053e+308,inf]となりますが、正しい値は1.797693134862315708145274237317049\cdots \times 10^{307}なので下端が真値より大きくなってしまっています。改修後は、
[8.9884656743115780417662938029053e+307,8.9884656743115780417662938029054e+307] [8.9884656743115790396864485702651e+307,8.9884656743115790396864485702652e+307] [1.797693134862315708145274237317e+308,inf]と正しく計算されていることが分かります。
2.の問題は、例えば(x_1,x_2)=(2^{1023},2^{970}), (y_1,y_2)=(2^{1023}-2^{971},2^{969}-2^{916})という入力で発生します。
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
int main()
{
std::cout.precision(32);
kv::interval<kv::dd> x, y, z;
x.lower().a1 = pow(2., 1023);
x.lower().a2 = pow(2., 970);
x.upper() = x.lower();
std::cout << x << "\n";
y.lower().a1 = pow(2., 1023) - pow(2., 971);
y.lower().a2 = pow(2., 969) - pow(2., 916);
y.upper() = y.lower();
std::cout << y << "\n";
z = x + y;
std::cout << z << "\n";
}
これを実行すると、改修前は[8.988465674311580536566680721305e+307,8.9884656743115805365666807213051e+307] [8.9884656743115780417662938029052e+307,8.9884656743115780417662938029053e+307] [inf,inf]のように[inf,inf]という不正な区間が発生していましたが、改修後は
[8.988465674311580536566680721305e+307,8.9884656743115805365666807213051e+307] [8.9884656743115780417662938029052e+307,8.9884656743115780417662938029053e+307] [1.797693134862315807937289714053e+308,inf]のように[ddの最大数、inf]という正しい結果を返すようになりました。
3.の問題は、区間演算では発生しないのですが、add_downを明示的に呼ぶと再現できます。
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
int main()
{
std::cout.precision(32);
kv::dd x, y, z;
x = std::numeric_limits<kv::dd>::infinity();
std::cout << x << "\n";
y = 0;
std::cout << y << "\n";
z = kv::rop<kv::dd>::add_down(x, y);
std::cout << z << "\n";
}
これを実行すると、inf 0 1.797693134862315807937289714053e+308のようにinf+0の下向き丸めが正の最大数になってしまいますが、改修でちゃんと
inf 0 infと正常になりました。
以前からこのバグには気付いていたのですが、多忙でなかなか改修できず、モヤモヤした気分が続いていました。確率が低いとはいえ、「精度保証が保証になっていない」バグを放置してはならないと考えていますので。しかし、double-double絡みのバグが目立つのは困りものです。針の穴を通すような繊細さが要求されると感じています。