前者は、作れそうだから作ってみただけ、というレベルで、 速度、精度ともに不十分と考えている。 内部では、psa型の係数にpsa型を持たせたものを用いている。 また、わずかな変更で三角形領域での精度保証が可能だったので、 それも作ってみた。
後者は、前者よりは計算速度でいくらかマシになった。
また、
使っているアルゴリズムは、 精度保証付き二重積分の方法まとめ (Version: 2019/11/20) の第2節に説明がある。
使い方は、
doubleintegral(被積分関数, x1, x2, y1, y2, 次数, 分割数)のような感じ。戻り値が計算結果。
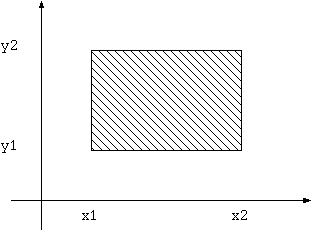
x1, x2, y1, y2はinterval型で、次の図のような積分範囲になる。

次数は用いる級数の次数、分割数をnとすると、x, yそれぞれをn等分して 計算する。
例えば、積分 \( \displaystyle \int_{-1}^1 \int_{-1}^1 \frac{1}{x^2 + 2y^2 +1} dx\,dy \) を計算する問題を考える。 このとき、次のようなプログラムを作成すればよい (sample2d1.cc)。
#include <kv/doubleintegral.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
typedef kv::interval<double> itv;
int main()
{
std::cout.precision(17);
std::cout << kv::doubleintegral(Func(), itv(-1), itv(1), itv(-1), itv(1), 8, 20) << "\n";
}
これを実行すると、
[2.2357751997649657,2.2357751999216653]のように表示される。
なお、
doubleintegral(被積分関数, x1, x2, y1, y2, 次数, 分割数, true)のように末尾にフラグtrueを設定すると、
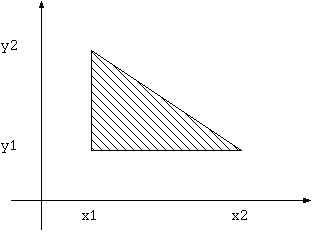
のような長方形の左下部分の三角形上の積分になる。 例えば、上の例に末尾trueを付けて (sample2d2.cc)、
#include <kv/doubleintegral.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
typedef kv::interval<double> itv;
int main()
{
std::cout.precision(17);
std::cout << kv::doubleintegral(Func(), itv(-1), itv(1), itv(-1), itv(1), 8, 20, true) << "\n";
}
は、積分
\(
\displaystyle \int_{-1}^1 \int_{-1}^{-y} \frac{1}{x^2 + 2y^2 +1} dx\,dy
\)
を計算する。実行すると、
[1.1178875998783734,1.1178875999649421]と表示される。
おまけで、
doubleintegral_triangle(被積分関数, x1, y1, x2, y2, x3, y3, 次数, 分割数)で、点(x1, y1)、点(x2, y2)、点(x3, y3)を頂点とする三角形上の 積分を行う。これは内部で変数変換してdoubleintegral(..., true)を呼び出している。
例えば、プログラム sample2d3.cc :
#include <kv/doubleintegral.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
typedef kv::interval<double> itv;
int main()
{
std::cout.precision(17);
std::cout << kv::doubleintegral_triangle(Func(), itv(-1), itv(-1), itv(-1), itv(1), itv(1), itv(-1), 8, 20) << "\n";
}
は、Sを点(-1, -1)、点(-1, 1)、点(1, -1)を頂点とする三角形として積分
\(
\displaystyle \iint_S \frac{1}{x^2 + 2y^2 +1} dx\,dy
\)
を計算する。実行すると
[1.1178875998793988,1.1178875999639196]と表示される。
一次元のものと同様、誤差項の計算に必要な高階微分の評価には
インクルードファイルは、double-newtoncotes.hppを使う。 また下請けとして、interval.hpp, highderiv.hpp, optimize.hpp または それらの下請けを使う。 参考ファイルはtest-double-newtoncotes.cc。
例えば、積分 \( \displaystyle \int_{-1}^1 \int_{-1}^1 \frac{1}{x^2 + 2y^2 +1} dx\,dy \) を計算するには、次のようなプログラムを作成すればよい (sample2d4.cc)。
#include <kv/double-newtoncotes.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
typedef kv::interval<double> itv;
int main()
{
std::cout.precision(17);
std::cout << kv::double_newtoncotes(Func(), itv(-1), itv(1), itv(-1), itv(1), 6, 0, 0) << "\n";
}
double_newtoncotesを呼び出す。引数は
double_newtoncotes(被積分関数, x1, x2, y1, y2, 分割区間の複合数, xの分割数, yの分割数, 誤差項の計算時の分割数)の意味。戻り値が計算結果。
実行すると、
[2.235775199814181,2.2357751998437357]と表示される。

アルゴリズムは、 精度保証付き二重積分について のp.42のように変数変換し、内部では上の 複合Newton-Cotes公式による長方形領域での二重積分を用いている。
インクルードファイルは、doubleint-curvededge.hppを使う。 下請けとして、double-newtoncotes.hpp、 それらの下請けを使う。 参考ファイルはtest-doubleint-curvededge.cc。
例えば、積分 \( \displaystyle \int_{-1}^1 \int_{-1 + \sin(3x) / 16}^{1 + \sin(5x) / 16} \frac{1}{x^2 + 2y^2 +1} \,dy\,dx \) を計算するには、次のようなプログラムを作成すればよい (sample2d5.cc)。
#include <iostream>
#include <kv/doubleint-curvededge.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
struct Edge_l {
template <class T> T operator() (const T& x) {
return -1 + sin(3*x) / 16;
}
};
struct Edge_h {
template <class T> T operator() (const T& x) {
return 1 + sin(5*x) / 16;
}
};
typedef kv::interval<double> itv;
int main() {
std::cout.precision(17);
std::cout << kv::doubleint_curvededge(Func(), Edge_l(), Edge_h(), itv(-1), itv(1), 6, 0, 0) << "\n";
}
doubleint_curvededgeを呼び出す。引数は
doubleint_curvededge(被積分関数, yの下端関数, yの上端関数, xの下端, xの上端, 分割区間の複合数, xの分割数, yの分割数, 誤差項の計算時の分割数)の意味で、積分範囲の指定以外の引数の意味は前のdouble-newtoncotes関数と同じ。
これを実行すると、
[2.2342787259328842,2.2342787260078528]と表示される。
また、xとyを入れ替えたdoubleint_curvededge_sも提供されている。 引数は
doubleint_curvededge_s(被積分関数, xの下端関数, xの上端関数, yの下端, yの上端, 分割区間の複合数, xの分割数, yの分割数, 誤差項の計算時の分割数)となる。
例えば、積分 \( \displaystyle \int_{-1}^1 \int_{-1 + \sin(3y) / 16}^{1 + \sin(5y) / 16} \frac{1}{x^2 + 2y^2 +1} \,dx\,dy \) を計算プログラムは次のようになる (sample2d6.cc)。
#include <iostream>
#include <kv/doubleint-curvededge.hpp>
struct Func {
template <class T> T operator() (const T& x, const T& y) {
return 1 / (x * x + 2 * y * y + 1);
}
};
struct Edge_l {
template <class T> T operator() (const T& x) {
return -1 + sin(3*x) / 16;
}
};
struct Edge_h {
template <class T> T operator() (const T& x) {
return 1 + sin(5*x) / 16;
}
};
typedef kv::interval<double> itv;
int main() {
std::cout.precision(17);
std::cout << kv::doubleint_curvededge_s(Func(), Edge_l(), Edge_h(), itv(-1), itv(1), 6, 0, 0) << "\n";
}
[2.2345032143918106,2.2345032147042741]