最終更新: 2018/12/11

初期値問題solverと射撃法による境界値問題の精度保証

柏木 雅英

1. はじめに

常微分方程式の初期値問題の精度保証を行うプログラムを利用して、 ストロボマップやポアンカレマップを作成し、それに対して (有限次元非線形方程式の) 精度保証を行うことで境界値問題に対する精度保証を 行える。

2. ファイル構成

strobomap.hpp (ストロボマップ)
poincaremap.hpp (ポアンカレマップ)
下請けとして、
ode-nv.hpp
ode-autodif-nv.hpp
ode-maffine.hpp
など。

3. ストロボマップの生成

ストロボマップは、初期値問題
dx/dt = f(x, t)
x(t0) = x0
に対して、終了時刻t1を定めたとき、初期値x0 に対してx(t1)を返す写像のことである。 初期値問題は、 「常微分方程式の初期値問題の精度保証」 の節で述べたように精度保証付きで解くことが出来る。 strobomap.hppは、その中のode_maffineを用いてストロボマップの (n次元ベクトルを受け取ってn次元ベクトルを返す)関数オブジェクトを 生成するものである。

初期値問題

dx0/dt = -x1+1
dx1/dt = x0-1
x0(0) = 0
x1(0) = 0
のx(1)を計算する問題に対して、直接ode_maffineを用いた場合と strobomapを用いた場合を比較したものを示す (sample-strobomap.cc)。 
#include <kv/ode-maffine.hpp>
#include <kv/strobomap.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;

struct Func {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = - x(1) + 1;
        y(1) = x(0) - 1;

        return y;
    }
};

int main()
{
    ub::vector<itv> ix;
    itv end;
    std::cout.precision(17);

    Func f;

    // use odelong_maffine

    ix.resize(2);
    ix(0) = 0;
    ix(1) = 0;
    end = 1.;
    kv::odelong_maffine(f, ix, (itv)0., end);
    std::cout << ix << "\n";

    // use Strobomap

    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);

    ix.resize(2);
    ix(0) = 0;
    ix(1) = 0;

    std::cout << g(ix) << "\n";
}
これを実行すると、 
[2]([1.3011686789397567,1.3011686789397572],[-0.38177329067603627,-0.38177329067603615])
[2]([1.3011686789397567,1.3011686789397572],[-0.38177329067603627,-0.38177329067603615])
のように全く同じ結果が得られる。

fが方程式の右辺を表す関数オブジェクト。 ode_maffineはfを呼び出しながら初期値問題を解く。 gは内部でode_maffineを呼び出して、ある時刻でのxの値を受け取って ある時刻でのxの値を返すような関数オブジェクト。 両者は全く同じ動作をするが、後者は余計なパラメータが全てオブジェクト内に 隠蔽されていて入出力がシンプルになっている。

関数オブジェクトgを生成している行、 

    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);
は、一般的には 
    kv::StroboMap<F,T> g(f, start, end, p);
の形で、 のような使い方。例えば内部で使う展開の次数を変更したいなら、 
    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1., kv::ode_param<double>().set_order(12));
のようにすればよい。

また、上記の例ではgの入力、出力の型は vector<interval<T>>で あったが、この関数はオーバーロードされていて、入出力として次のような型が 使える。

入出力の型 内部で使われている関数
vector<T> ode-nv.hppの中の関数odelong_nv (精度保証しない)
vector<autodif<T>> ode-autodif-nv.hppの中の関数odelong_nv (精度保証しない)
vector<interval<T>> ode-maffine.hppの中の関数odelong_maffine (「常微分方程式の初期値問題の精度保証」の(16))
vector<affine<T>>, ode-maffine.hppの中の関数odelong_maffine (「常微分方程式の初期値問題の精度保証」の(15))
vector<autodif<interval<T>>> ode-maffine.hppの中の関数odelong_maffine (「常微分方程式の初期値問題の精度保証」の(17))

このオーバーロードによって、gに対して例えば

を適用することが可能となる。 例えば、
x0(1) = 0
x1(1) = 0
となるような初期値を求めるプログラムは、次のようになる。 (sample-strobomap2.cc)。 Newton法を3回まわした後にKrawczyk法を使う。 
#include <kv/strobomap.hpp>
#include <kv/kraw-approx.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;

struct Func {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = - x(1) + 1;
        y(1) = x(0) - 1;

        return y;
    }
};

int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    bool r;

    std::cout.precision(17);

    Func f;

    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);

    x.resize(2);
    x(0) = 0;
    x(1) = -1;
    r = kv::krawczyk_approx(g, x, ix, 3);
    if (r) std::cout << "Solution Found\n";
}
実行結果は次のようになる。 
newton0: [2](-0.38177329067603671,1.301168678939757)
newton1: [2](-0.38177329067603621,1.3011686789397567)
newton2: [2](-0.38177329067603627,1.3011686789397567)
I: [2]([-0.38177329067603683,-0.38177329067603571],[1.3011686789397549,1.3011686789397586])
K: [2]([-0.38177329067603644,-0.38177329067603599],[1.3011686789397565,1.3011686789397572])
Solution Found

4. 境界値問題、周期解問題を解く

4.1 方程式の生成

前節でストロボマップの作成とそれを用いた方程式の求解について説明した。 ここで、例えばkrawczyk_approxは、与えられたgに対してg(x)=0を満たすxを 求める仕様なので、このままだと終了時刻で0になる初期値を求める問題しか 解けない。例えば先と同じ問題で終了時刻で(0,0)でなく(1,0)になるような 初期値を求める問題を解こうと思うと、ストロボマップから(1,0)を引くような 新しい関数オブジェクトを生成する必要がある。 例えば、次のようになる (sample-strobomap3.cc)。 
#include <kv/strobomap.hpp>
#include <kv/kraw-approx.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;

struct Func {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = - x(1) + 1;
        y(1) = x(0) - 1;

        return y;
    }
};

template <class F> struct Tmp {
    F f;
    Tmp(F f): f(f) {}
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
        ub::vector<T> y(2);
        y = f(x);
        y(0) -= 1.;
        y(1) -= 0.;
        return y;
    }
};

int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    bool r;

    std::cout.precision(17);

    Func f;
    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);
    Tmp< kv::StroboMap<Func,double> > h(g);

    x.resize(2);
    x(0) = 0;
    x(1) = 0.5;
    r = kv::krawczyk_approx(h, x, ix, 3);
    if (r) std::cout << "Solution Found\n";
}
計算すると次のようになる。 
newton0: [2](0.15852901519210344,0.45969769413186035)
newton1: [2](0.15852901519210344,0.45969769413186035)
I: [2]([0.15852901519210299,0.15852901519210389],[0.45969769413185967,0.45969769413186102])
K: [2]([0.15852901519210318,0.15852901519210369],[0.45969769413186001,0.45969769413186068])
Solution Found
gを元にTmpというクラスを使って新しい関数オブジェクトhを作っている。

このやり方で様々な境界値問題を解くことが出来るが、面倒なので いくつか代表的な形の問題に対するヘルパークラスがある。 以下、それを説明する。

4.2 周期解

まず、周期解を求めるサンプルを示す。 kv/strobomap.hppの中に、次のようなクラス定義がある。 
template <class F> class FixedPoint {
    public:
    F f;
    FixedPoint(F f) : f(f) {}
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
        return x - f(x);
    }
};
引数として与えたfから、x-f(x)を計算する関数オブジェクトを生成する。

これを用いて、Duffing方程式

d2x/dt2 = - 0.125 * dx/dt - x3 + 0.5 * cos(t)
を連立化した
dx0/dt = x1
dx1/dt = - 0.125 * x1 - x03 + 0.5 * cos(t)
の2π周期解を求めるプログラムを示す。 (sample-strobomap4.cc)。 
#include <kv/strobomap.hpp>
#include <kv/kraw-approx.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;


struct Duffing {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = x(1);
        y(1) = - 0.125 * x(1) - x(0)*x(0)*x(0) + 0.5 * cos(t);

        return y;
    }
};

int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    bool r;

    std::cout.precision(17);

    Duffing f;

    kv::StroboMap<Duffing,double> g(f, (itv)0., kv::constants<itv>::pi() * 2.);

    kv::FixedPoint< kv::StroboMap<Duffing,double> > h(g);

    x.resize(2);
    x(0) = 1.27;
    x(1) = 0.68;
    r = kv::krawczyk_approx(h, x, ix, 3);
    if (r) std::cout << "Solution Found\n";
}
gがDuffing方程式を2π進める関数オブジェクト、hはh(x)=x-g(x)である。

計算結果は以下の通り。 

newton0: [2](1.2708913903607826,0.67994418970433268)
newton1: [2](1.2708908549501272,0.67994428153814435)
newton2: [2](1.270890854949962,0.67994428153814046)
I: [2]([1.2708908549499433,1.2708908549499807],[0.67994428153811836,0.67994428153816256])
K: [2]([1.2708908549499535,1.2708908549499707],[0.67994428153812846,0.67994428153815057])
Solution Found
これで、Duffing方程式の周期解の存在が数学的に厳密に証明されたことになる。

4.3 2点境界値問題

次に、2点境界値問題を解く例を示す。
d2x/dt2 = x3 - 3
x(0) = x(1) = 0
を連立化した
dx0/dt = x1
dx1/dt = - x03 - 3
x0(0) = x0(1) = 0
を解くことを考える。 これを解く場合、一般的には、 「x0(0)は0に固定し、x1(0)を変化させながら何度も初期値問題を解いてx0(1)の値が0になるようにする。」 という方針になる。 4.1節のようにしてこの方程式を作成できるが、ヘルパークラスとして Shooting_TPBVPを用意した。
Shooting_TPBVP<F,T> h(g, start_value, end_value, start_index, end_index)
のようにして初期時刻から終端時刻までのストロボマップgから、2点境界値問題を 射撃法で解くための方程式hを作成できる。 この場合、t0を初期時刻、t1を終端時刻として、
xstart_index(t0)=start_value
xend_index(t1)=end_value
を固定して、xの添字のうちstart_indexで無い方を未知数として動かす。 すなわち、start_indexやend_indexを1にすれば、端点の微分を固定するような タイプの境界値問題も解くことが出来る。 ただし、Fはgの型、Tはstart_value, end_valueの型である。

上の例題を解くプログラムは、次のようになる (sample-strobomap5.cc)。 

#include <kv/strobomap.hpp>
#include <kv/kraw-approx.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;


struct Func {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = x(1);
        y(1) = - x(0)*x(0)*x(0) - 3.;

        return y;
    }
};

int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    int r;

    std::cout.precision(17);

    Func f;

    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);

    kv::Shooting_TPBVP< kv::StroboMap<Func,double>, double> h(g, 0., 0., 0, 0);

    x.resize(1);
    x(0) = 1.5; 
    r = kv::krawczyk_approx(h, x, ix, 3);
    if (r) std::cout << ix << "\n";
}
実行結果は次の通り。 
newton0: [1](1.5124622710966928)
newton1: [1](1.5124739655034052)
newton2: [1](1.5124739655138593)
I: [1]([1.5124739655138577,1.5124739655138609])
K: [1]([1.5124739655138583,1.51247396551386])
[1]([1.5124739655138583,1.51247396551386])

5. ポアンカレマップ

自励系 (右辺に時刻tを含まない) 常微分方程式の周期解を計算する ことを考える。 例えば、van der Pol方程式
d2x/dt2 = 1 * (1 - x2) * dx/dt - x;
の周期解を求める。

このような問題には、次のような難しさがある。

後者を解決するため、t=0で解がある平面 (必ずしも平面でなくてもよいが) に 乗っているような解を計算することにする。この平面から出発して、 この平面に戻ってきた時の値を計算し、それが初期点と一致することを 確認する。このような平面をポアンカレ断面と呼ぶ。

後者を解決するため、周期Tを未知数としてこれも初期点とともに 求解の対象に含めることにする。 初期点の座標をx, 周期をp、ポアンカレ断面を表す式をs(x)=0、 xから初期値問題をt=Tまで解いたときの値を返す関数を φT(x)としたとき、連立方程式

x - φp(x) = 0
s(x) = 0
を解けばよい。 これに対してKrawczyk法を適用するには、この関数がpで微分できる 必要があるが、φをpで微分したものは元の微分方程式の右辺fに 時刻pまで解いた解x(p)を代入したf(x(p), p)として簡単に求まる。

微分方程式の右辺を表す関数オブジェクトからこの連立方程式の 関数オブジェクトを生成するヘルパークラスPoincareMapを用意した。

kv::PoincareMap<F,S,T> po(f, s, t, p)
先の問題を解くプログラムを示す (sample-strobomap6.cc)。 
#include <kv/poincaremap.hpp>
#include <kv/kraw-approx.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;

struct VDP {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = x(1);
        y(1) = 1. * (1. - x(0)*x(0)) * x(1) - x(0);

        return y;
    }
};

struct VDPPoincareSection {
    template <class T> T operator() (const ub::vector<T>& x){
        T y;

        y = x(0) - 0.;

        return y;
    }
};


int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    bool r;

    std::cout.precision(17);

    VDP f;
    VDPPoincareSection ps;
    kv::PoincareMap<VDP,VDPPoincareSection,double> po(f, ps, (itv)0.);

    x.resize(3);
    x(0) = 0.; 
    x(1) = 2.;
    x(2) = 6.;

    r = kv::krawczyk_approx(po, x, ix, 5);
    if (r) {
        std::cout << "solution found.\n";
        std::cout << ix << "\n";
    }
}
実行結果は以下の通り。 
newton0: [3](0,2.0227495144851573,6.865064908408975)
newton1: [3](0,2.3540976972945398,6.720203568801864)
newton2: [3](-4.6365776638536575e-17,2.172950117305227,6.6622372888869803)
newton3: [3](-3.540672660497554e-19,2.1727150104494624,6.6632877739672525)
newton4: [3](-1.9436003875826564e-22,2.1727136926229509,6.6632868593233372)
I: [3]([-2.2545934104027633e-13,2.2545934065155625e-13],[2.1727136926222767,2.1727136926236251],[6.6632868593228833,6.6632868593237911])
K: [3]([-2.1564561824136069e-28,9.6433518152068958e-29],[2.1727136926225014,2.1727136926225917],[6.663286859323108,6.6632868593231516])
solution found.
[3]([-2.1564561824136069e-28,9.6433518152068958e-29],[2.1727136926225014,2.1727136926225917],[6.663286859323108,6.6632868593231516])

これにより、点 ([-2.1564561824136069e-28,9.6433518152068958e-29],[2.1727136926225014,2.1727136926225917]) を通る周期 [6.663286859323108,6.6632868593231516] の周期解の存在が保証されたことになる。

6. 全解探索

ここまでの例は、Krawczyk法で解を一つ求めるものばかりだったが、 計算時間は大変だが、全解探索をさせることも出来る。 4.3の2点境界値問題の例題で、未知数として動かす x1(0) (=x'(0))の範囲を[-100,100]として全探索を行う プログラムを示す (sample-strobomap7.cc)。 
#include <kv/strobomap.hpp>
#include <kv/allsol.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;


struct Func {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = x(1);
        y(1) = - x(0)*x(0)*x(0) - 3.;

        return y;
    }
};

int main()
{
    ub::vector<itv> ix;

    std::cout.precision(17);

    Func f;

    kv::StroboMap<Func,double> g(f, (itv)0., (itv)1.);

    kv::Shooting_TPBVP< kv::StroboMap<Func,double>, double> h(g, 0., 0., 0, 0);

    ix.resize(1);
    ix(0) = itv(-100., 100.); 
    kv::allsol(h, ix, 2);
}
実行すると、次のようになる。 
[1]([1.3426250685230762,1.6485216506336593])(ex): 0, giveup: 0    
[1]([1.5124739655138583,1.51247396551386])(ex:improved)
[1]([-9.7287985107793933,-9.6649560440004425])(ex) 1, giveup: 0    
[1]([-9.6820098794439336,-9.682009879443898])(ex:improved)
[1]([9.6546315277184042,9.7009268065571189])(ex)x: 2, giveup: 0    
[1]([9.6695050644435625,9.6695050644435928])(ex:improved)
[1]([-38.891558638109978,-38.887056483138387])(ex)3, giveup: 0     
[1]([-38.889039294217483,-38.889039294217255])(ex:improved)
[1]([38.886946442501269,38.891417685282584])(ex): 4, giveup: 0    
[1]([38.889039294217248,38.889039294217469])(ex:improved)
[1]([-87.506327790375452,-87.506193234670092])(ex)5, giveup: 0    
[1]([-87.506260512712828,-87.506260512712103])(ex:improved)
[1]([87.506191617784267,87.506325723414094])(ex): 6, giveup: 0    
[1]([87.506258670770876,87.506258670771616])(ex:improved)
ne_test: 197, ex_test: 9, ne: 89, ex: 7, giveup: 0
この範囲に7つの解が存在することが証明された。

7. その他

7.1 解軌道の描画の例

得られた解軌道を描いたりするには、精度保証された初期値を用いて 改めてodelong_maffine等を用いて初期値問題を解けばよい。 例えば、5.で得られたvan der Pol方程式の周期解を描画する 例を示す (sample-strobomap8.cc)。 
#include <kv/poincaremap.hpp>
#include <kv/kraw-approx.hpp>
#include <kv/ode-maffine.hpp>

namespace ub = boost::numeric::ublas;

typedef kv::interval<double> itv;

struct VDP {
    template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
        ub::vector<T> y(2);

        y(0) = x(1);
        y(1) = 1. * (1. - x(0)*x(0)) * x(1) - x(0);

        return y;
    }
};

struct VDPPoincareSection {
    template <class T> T operator() (const ub::vector<T>& x){
        T y;

        y = x(0) - 0.;

        return y;
    }
};


int main()
{
    ub::vector<double> x;
    ub::vector<itv> ix;
    int i;
    bool r;

    std::cout.precision(17);

    VDP f;
    VDPPoincareSection ps;
    kv::PoincareMap<VDP,VDPPoincareSection,double> po(f, ps, (itv)0.);

    x.resize(3);
    x(0) = 0.; 
    x(1) = 2.;
    x(2) = 6.;

    r = kv::krawczyk_approx(po, x, ix, 5, 0);
    if (!r) return 0;

    std::list< kv::interval<double> > time_list;
    std::list< ub::vector< kv::interval<double> > > value_list;
    ub::vector<itv> ix2;
    itv end;

    ix2.resize(2);
    ix2(0) = ix(0);
    ix2(1) = ix(1);
    end = ix(2);

    r = kv::odelong_maffine(f, ix2, itv(0.), end, kv::ode_param<double>(), kv::ode_callback_dense_list<double>(itv(0.), itv(0.05), time_list, value_list)); 

    time_list.push_back(end);
    value_list.push_back(ix2);

    std::list< kv::interval<double> >::iterator pt;
    std::list< ub::vector< kv::interval<double> > >::iterator pv;
    pt = time_list.begin();
    pv = value_list.begin();

    while (pt != time_list.end()) {
        std::cout << mid(*pt) << " ";
        for (i=0; i<2; i++) {
            std::cout << mid((*pv)(i)) << " ";
        }
        std::cout << "\n";
        pt++; pv++;
    }
}
初期値を求まった不動点に、終了時刻を周期に設定し、 odelong_maffineで再計算させている。このとき、 「常微分方程式の初期値問題の精度保証」の節の callbackのところで述べたode_callback_dense_listを使って、 リストの形で間隔0.05で密出力させている。 そのリストを元に、全ての値の中心を表示している。

これを実行すると、 

0 -2.3795713510718954e-29 2.1727136926225468 
0.050000000000000003 0.11134528041917739 2.280837733915992 
0.10000000000000001 0.22802773346910427 2.3855656135053023 
0.15000000000000002 0.34977377020615608 2.4825750959546031 
0.20000000000000001 0.47606831242003711 2.5665395328594327 
0.25 0.60610764565154129 2.6312823070207707 
0.30000000000000004 0.73876519169977151 2.6701477490940784 
0.34999999999999998 0.87258200940473429 2.6766207394721966 
0.40000000000000002 1.0057940765936335 2.6451669471554866 
0.45000000000000007 1.1364048895519248 2.5721781158737911 
0.5 1.2623038667093454 2.4568195351627082 
0.55000000000000004 1.3814195797313349 2.3015358723720483 
0.60000000000000009 1.491885412130264 2.1120190285979583 
0.65000000000000013 1.5921886249871131 1.8965825596914434 
0.69999999999999996 1.6812756258032397 1.6650713090950264 
0.75 1.7585965920994835 1.4275780848725521 
0.80000000000000004 1.8240876057409938 1.1932752061839977 
0.85000000000000009 1.8781023048623271 0.96959120148093825 
0.90000000000000013 1.9213131937119636 0.76182335898051368 
0.94999999999999996 1.9546038252370144 0.57314461291358443 
1 1.9789687570339238 0.40488436471927008 
1.0500000000000003 1.9954314907343538 0.25694515546221536 
1.1000000000000001 2.0049841970099926 0.12824182226387526 
1.1499999999999999 2.0085483736367751 0.017091196777383619 
1.2000000000000002 2.0069529986924151 -0.078480559149065321 
1.25 2.000925844466813 -0.16051806603303653 
1.3000000000000003 1.9910937996489184 -0.23099378948718158 
1.3500000000000001 1.97798875762468 -0.29172540360141119 
1.3999999999999999 1.9620564871487711 -0.34433645531543122 
1.4500000000000002 1.943666696723946 -0.39024580471392312 
1.5 1.9231231471205132 -0.43067468142416887 
1.5500000000000003 1.9006731420916909 -0.46666341813064727 
1.6000000000000001 1.8765160553698195 -0.49909256884164432 
1.6499999999999999 1.850810764362917 -0.52870510353848477 
1.7000000000000002 1.8236819893581773 -0.55612776333183733 
1.75 1.7952256080170212 -0.58189058599615329 
1.8000000000000003 1.7655130486545718 -0.60644419635745617 
1.8500000000000001 1.7345948765580221 -0.6301748047034067 
1.8999999999999999 1.7025036851056772 -0.6534170491592971 
1.9500000000000002 1.6692563939837264 -0.67646491192494151 
2 1.6348560442644089 -0.69958097329216629 
2.0499999999999998 1.5992931668195891 -0.72300426694212527 
2.1000000000000005 1.562546787786244 -0.74695698122606302 
2.1500000000000004 1.5245851232298835 -0.77165022365862945 
2.2000000000000002 1.4853660050512003 -0.79728903518597261 
2.25 1.4448370716322114 -0.82407680967851693 
2.2999999999999998 1.4029357497129573 -0.85221924350152234 
2.3500000000000005 1.359589048504664 -0.88192790969319179 
2.4000000000000004 1.31471318309125 -0.91342352010532069 
2.4500000000000002 1.2682130418346156 -0.94693890495954103 
2.5 1.2199815119791739 -0.98272170000902392 
2.5499999999999998 1.169898679299278 -1.0210366833642168 
2.6000000000000005 1.1178309220025184 -1.0621676424631969 
2.6500000000000004 1.0636299270061733 -1.1064185707353038 
2.7000000000000002 1.0071316692915828 -1.1541138857131772 
2.75 0.94815541388007374 -1.2055972163825306 
2.7999999999999998 0.8865028271431159 -1.2612281163393275 
2.8500000000000005 0.82195732232572682 -1.3213758085691842 
2.9000000000000004 0.75428381660579769 -1.3864087455448573 
2.9500000000000002 0.68322914752292485 -1.4566783671196728 
3 0.60852348912544518 -1.5324949618078425 
3.0499999999999998 0.52988322594187098 -1.6140930116994028 
3.1000000000000005 0.44701588675135634 -1.7015828993783872 
3.1500000000000004 0.35962790561945951 -1.7948855255227223 
3.2000000000000002 0.26743615003330568 -1.8936464983405605 
3.25 0.17018430285106687 -1.9971275539715632 
3.2999999999999998 0.067665246386478528 -2.1040754081456488 
3.3500000000000005 -0.040249524635957115 -2.2125731799112511 
3.4000000000000004 -0.15357288210215253 -2.3198877623596372 
3.4500000000000002 -0.27215781007268641 -2.4223385382739 
3.5 -0.39564792954897171 -2.5152279000395863 
3.5499999999999998 -0.52342722166990252 -2.5928888906339109 
3.6000000000000005 -0.65457637685233305 -2.6489129954357926 
3.6500000000000004 -0.78784619671923839 -2.6766110683288797 
3.7000000000000002 -0.92166028907280506 -2.6697214138796834 
3.75 -1.0541583247221036 -2.6233070637876343 
3.7999999999999998 -1.1832859550547135 -2.5346924078965016 
3.8500000000000005 -1.3069279299176586 -2.4042132488499472 
3.9000000000000004 -1.423068996257346 -2.2355422276426316 
3.9500000000000002 -1.5299569430840336 -2.0354356360602566 
4 -1.6262383604919624 -1.8129129073987658 
4.0500000000000007 -1.7110428495059438 -1.5780592272833887 
4.0999999999999996 -1.7840041013121803 -1.3407506044351982 
4.1500000000000004 -1.8452215190075358 -1.1095921663633879 
4.2000000000000011 -1.8951781872315143 -0.89125213399626202 
4.25 -1.9346365075233019 -0.69022954243840395 
4.3000000000000007 -1.9645316058191082 -0.50897782695515659 
4.3499999999999996 -1.985877070886739 -0.34825089751743199 
4.4000000000000004 -1.9996907421041334 -0.20753916241425857 
4.4500000000000011 -2.0069423983815549 -0.085496631913519749 
4.5 -2.0085213165509517 0.01969755043478608 
4.5500000000000007 -2.0052197672042573 0.11006435623197916 
4.5999999999999996 -1.9977280873185532 0.18763494669908085 
4.6500000000000004 -1.9866374007390557 0.25433191679594169 
4.7000000000000011 -1.9724468567562776 0.31190443624857062 
4.75 -1.9555731090986581 0.36190099295875328 
4.8000000000000007 -1.9363605023782902 0.40566641708559226 
4.8499999999999996 -1.9150910139076291 0.44435325802708853 
4.9000000000000004 -1.8919934169245709 0.47894062349376854 
4.9500000000000011 -1.8672514129466078 0.51025599197886407 
5 -1.8410106590194297 0.53899726402832404 
5.0500000000000007 -1.8133847201909865 0.56575352357860198 
5.0999999999999996 -1.784460032827849 0.59102376738162476 
5.1500000000000004 -1.754299988283281 0.6152333476400661 
5.2000000000000011 -1.7229482514014791 0.6387481564358003 
5.25 -1.6904314227060144 0.66188673146708654 
5.3000000000000007 -1.6567611421745201 0.68493053084920452 
5.3499999999999996 -1.6219357194864468 0.70813264372667073 
5.4000000000000004 -1.5859413624271914 0.73172519480512865 
5.4500000000000011 -1.5487530627583881 0.75592567806433553 
5.5 -1.5103351878140159 0.78094242580053297 
5.5500000000000007 -1.4706418165480986 0.80697938810775738 
5.5999999999999996 -1.4296168507805849 0.83424036694613535 
5.6500000000000004 -1.3871939259427264 0.86293281852838721 
5.7000000000000011 -1.3432961406957611 0.8932713072915266 
5.75 -1.2978356214213798 0.92548066280142383 
5.8000000000000007 -1.2507129358826088 0.95979885541645871 
5.8499999999999996 -1.2018163705794294 0.99647956447665242 
5.9000000000000004 -1.1510210888940189 1.035794360312962 
5.9500000000000011 -1.0981881926771013 1.0780343534533143 
6 -1.043163719396885 1.1235110745729839 
6.0500000000000007 -0.98577762164733651 1.1725562288432614 
6.0999999999999996 -0.92584279743841968 1.2255198083893946 
6.1500000000000004 -0.863154270554781 1.2827658349457143 
6.2000000000000011 -0.79748866326518253 1.3446647291044163 
6.25 -0.72860416228206693 1.4115809519017755 
6.3000000000000007 -0.65624125701473246 1.4838541341737086 
6.3499999999999996 -0.58012463064419872 1.5617714094623378 
6.4000000000000004 -0.4999667119928215 1.6455281379268407 
6.4500000000000011 -0.41547354890405008 1.7351737474316975 
6.5 -0.32635383432349974 1.8305392112269443 
6.5500000000000007 -0.23233208426178131 1.9311430569401367 
6.5999999999999996 -0.133167091135102 2.0360742778902772 
6.6500000000000004 -0.028676784021194723 2.1438538326734951 
6.6632868593231311 3.0531133177191805e-15 2.1727136926225499
のように出力される (sample-strobomap8.dat)。 これに対して、gnuplotで例えば 
set size ratio -1
set grid
plot "sample-strobomap8.dat" using 2:3 with lines notitle
のようにすれば、

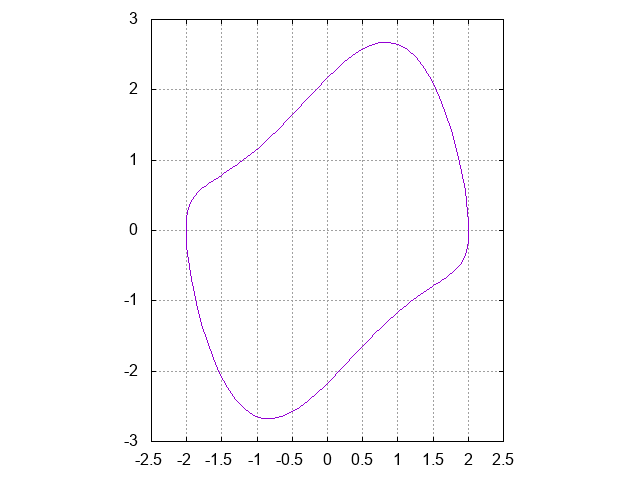
のような軌道の図が得られる。

7.2 何書こうかな

まだ書いてない。