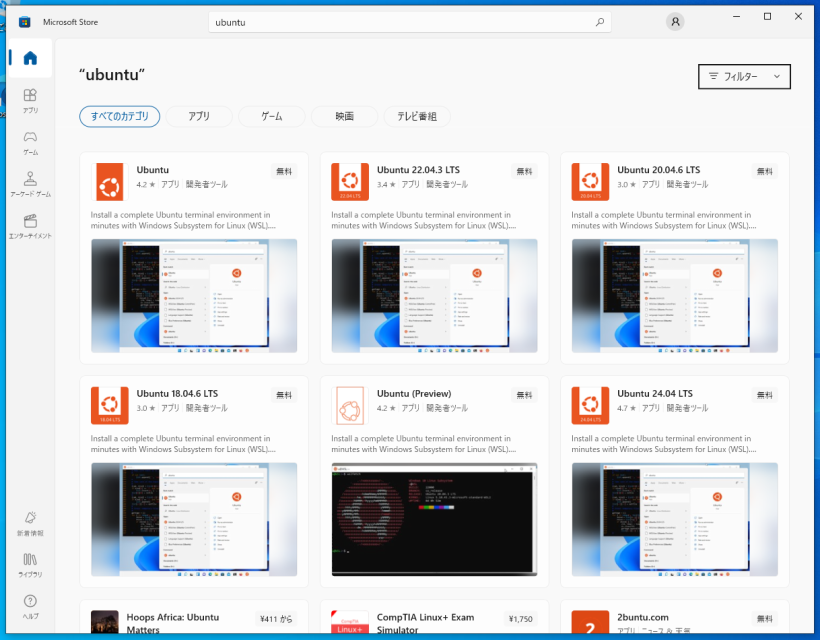
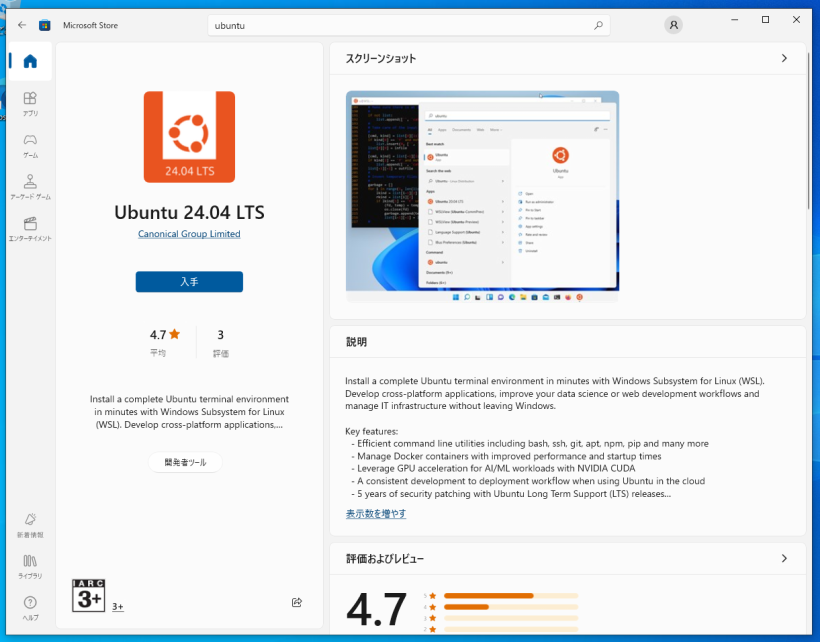
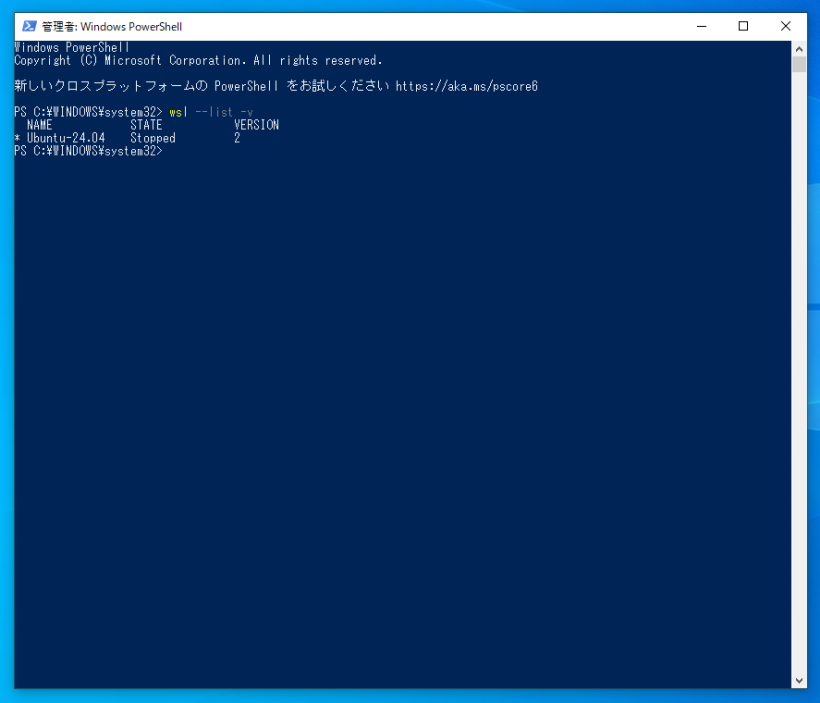
Ubuntu 24.04 インストールシリーズのオマケとして、Windows 10/11のWSL2のインストールについて書いてみます。bash on Ubuntu on Windowsを試してみる の記事以来です。当時はまだWSLとは呼ばれていませんでした。WSL1からWSL2になって仮想マシンを使うようになって性能及び互換性が向上し、またWSL-gとなってX serverを別にインストールしなくてもGUIアプリを動かすことができるようになりました。ちょうどWSL2の中に入れられるLinuxとしてUbuntu 24.04も出たので、ここらでインストール方法についてまとめてみました。Windows 10でもWindows 11でも基本的には同じと思いますが、まっさらなWindows 10に入れてみました。
WSL2になって仮想マシンを使うようになって性能が向上したのですが、それと引き換えに、VT-xと呼ばれる機能をBIOS(正確にはUEFI?)で有効にする必要があります。ほとんどのマシンで有効になっているとは思いますが、もしなっていない場合、BIOSに入って有効にする必要があります。入り方はマシン毎に千差万別なので説明のしようもありませんが、起動時にDEL連打、もしくはF2連打のマシンが多い気がします。うまくBIOSに入れたら、Intel VT-x (Intel CPUの場合) もしくはAMD-V Virtualization (AMD CPUの場合)を探してオンにして下さい。
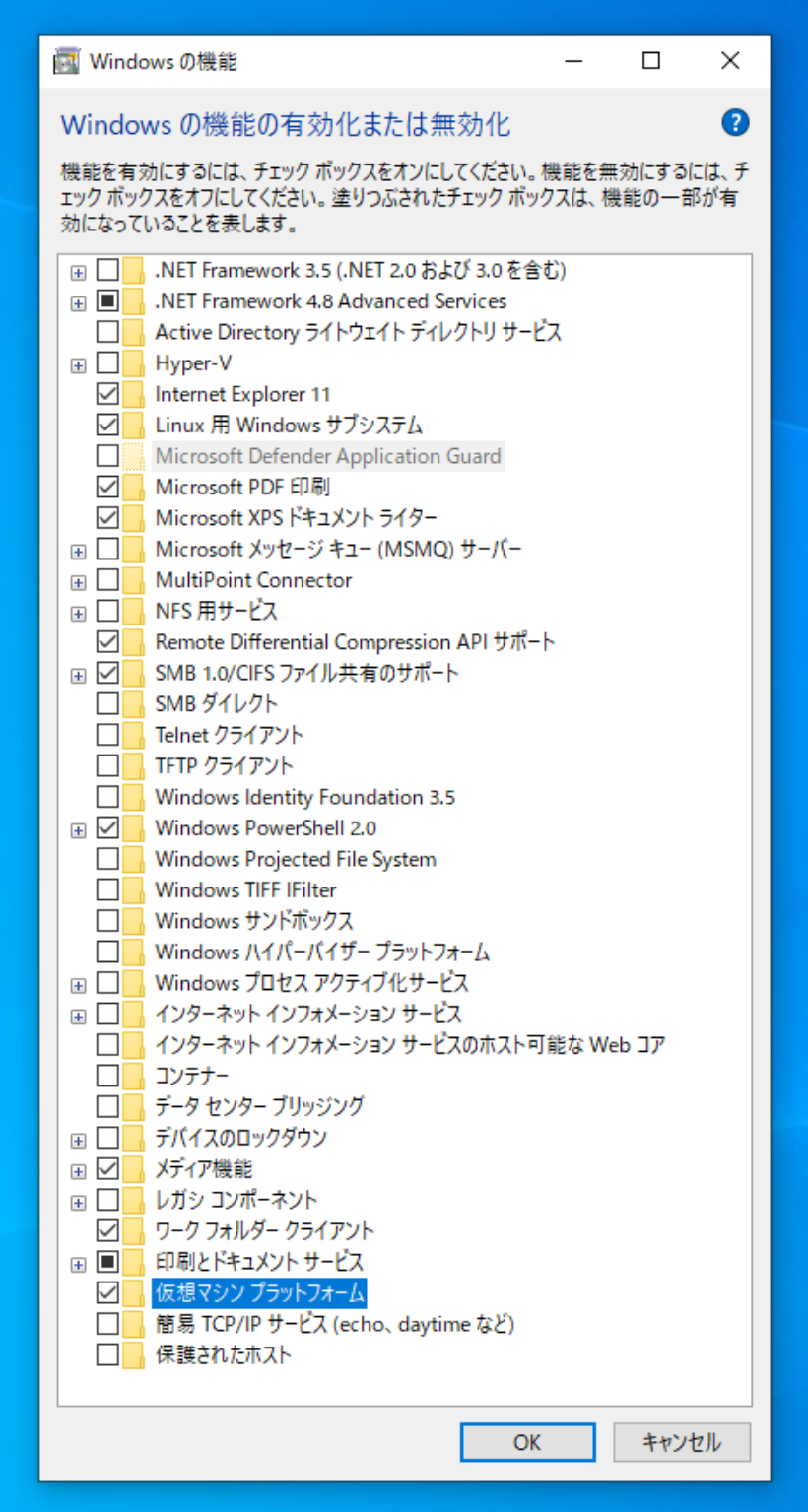
Linux用Windowsサブシステム
仮想マシンプラットフォーム
の2つにチェックを入れて再起動する必要があります。
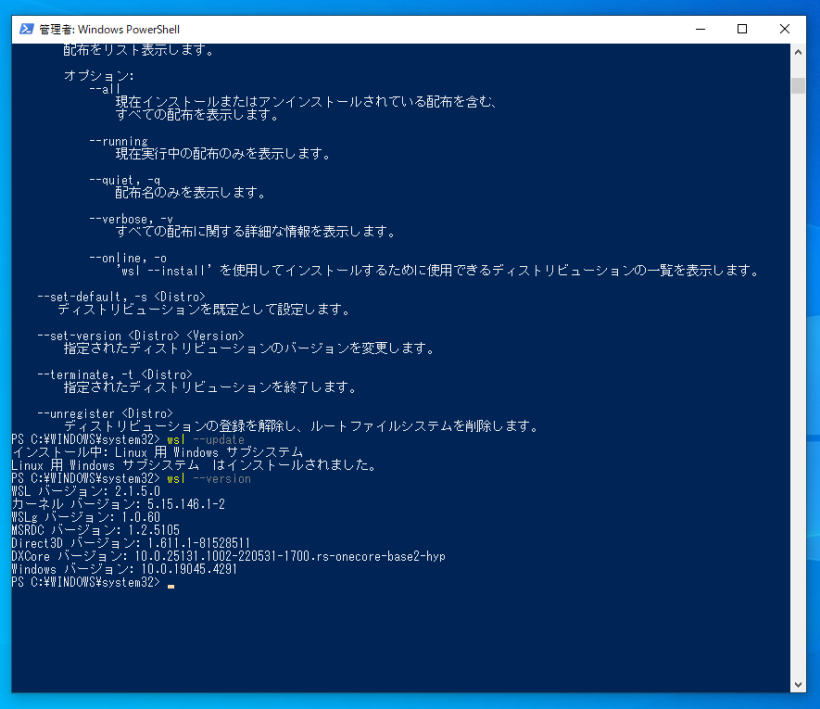
WSL バージョン: 2.1.5.0
カーネル バージョン: 5.15.146.1-2
WSLg バージョン: 1.0.60
MSRDC バージョン: 1.2.5105
Direct3D バージョン: 1.611.1-81528511
DXCore バージョン: 10.0.25131.1002-220531-1700.rs-onecore-base2-hyp
Windows バージョン: 10.0.19045.4291
になりました。
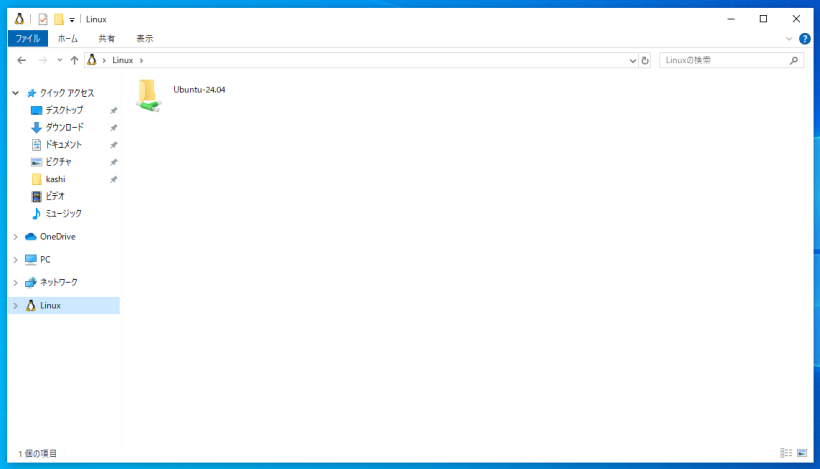
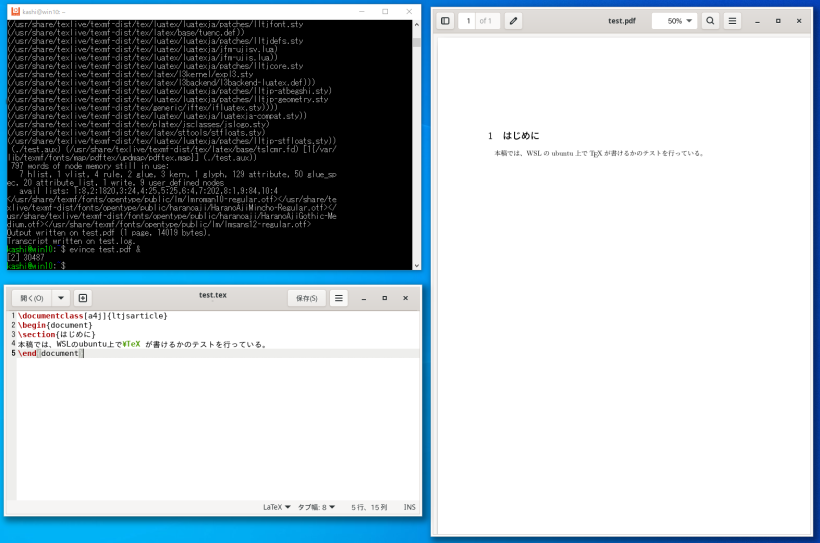
この状態で、Windows側からWSL側のファイルを見るには、エクスプローラに追加されている「Linux」という項目を使うことができます。
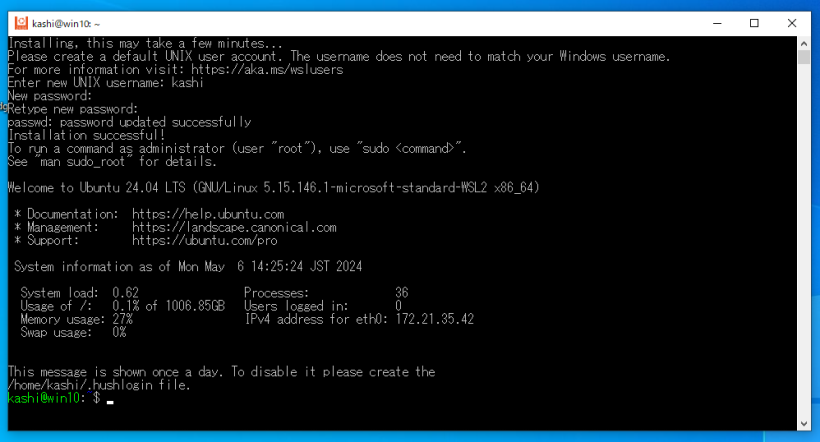
ここから必要なアプリケーションをaptコマンドを使って追加していきますが、その前に絶対必要な作業があります。WSLのターミナルで、
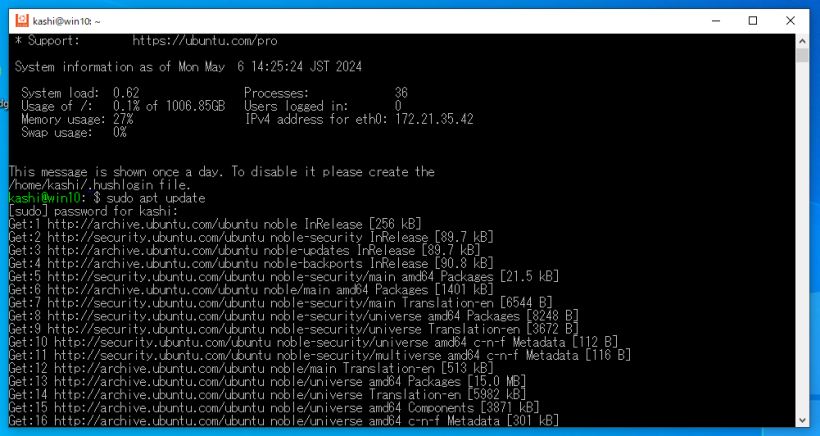
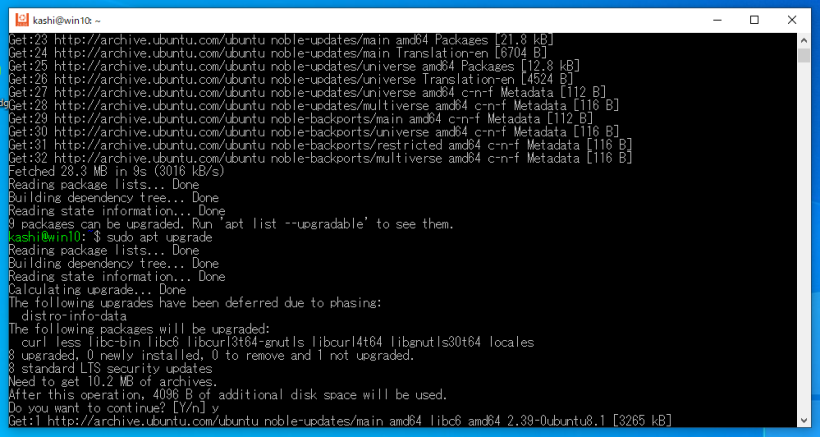
sudo apt update
sudo apt upgrade
として、Ubuntu 24.04を最新にしてください。特に最初の1行が重要で、これをやらないとこの先のaptコマンドでのインストールが失敗してしまいます。
sudo apt install -y language-pack-en
sudo apt install -y language-pack-ja
sudo update-locale LANG=ja_JP.UTF8
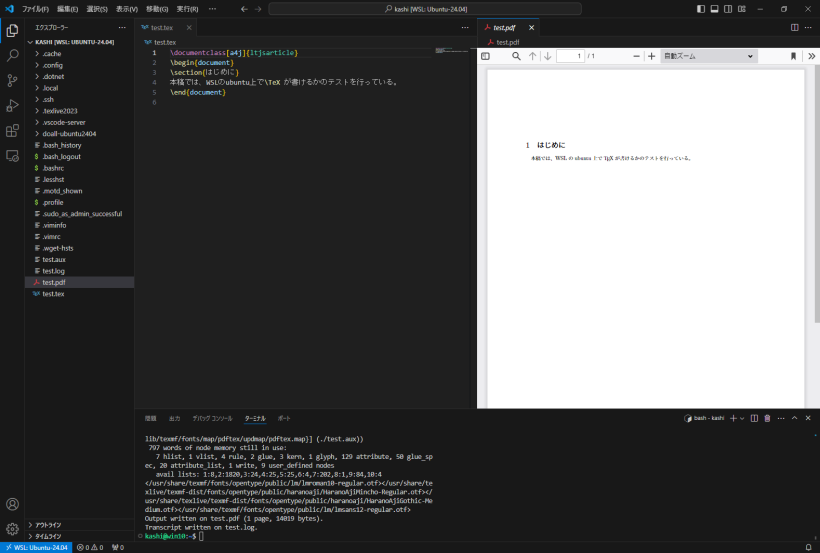
として、いったんWSLターミナルを閉じて再度スタートメニューから起動します。language-pack-enの方はすぐには不要かもですが、無いと何かと不便なのでこちらもついてに入れておきます。自分の環境では、Visual Studio CodeでのWSLターミナルで問題が発生しました。Ubuntu 24.04 インストール (リンク集) のうちからapache, sambaなどを除き、適当に抜粋して次のようなものを入れてみました。
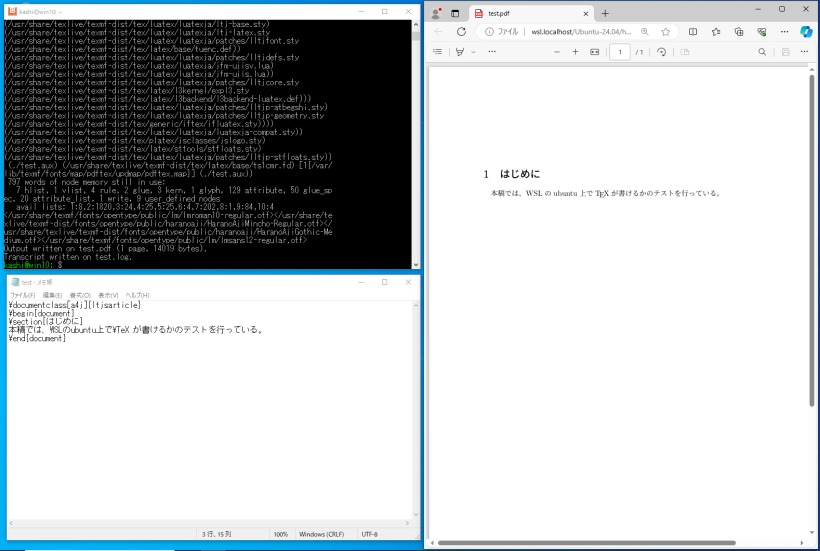
sudo apt install -y texlive-full
sudo apt install -y nkf
sudo apt install -y gnuplot
sudo apt install -y tgif
sudo apt install -y pdfarranger
sudo apt install -y pdftk-java
sudo apt install -y build-essential
sudo apt install -y clang
sudo apt install -y libboost-all-dev
sudo apt install -y default-jdk
sudo apt install -y lua5.4
sudo apt install -y liblua5.4-dev
sudo apt install -y luajit
sudo apt install -y gfortran
sudo apt install -y python3
sudo apt install -y python3-dev
sudo apt install -y python3-numpy
sudo apt install -y python3-scipy
sudo apt install -y python3-matplotlib
sudo apt install -y python3-sympy
sudo apt install -y python3-mpmath
sudo apt install -y ipython3
sudo apt install -y python-is-python3
sudo apt install -y octave
sudo apt install -y octave-dev
sudo apt install -y libgmp-dev
sudo apt install -y libmpfr-dev
sudo apt install -y gcc-multilib
sudo apt install -y g++-multilib
sudo apt install -y nim
sudo apt install -y lv
この段階でも、
メモ帳等、任意のwindowsのエディタ
(抵抗が無ければ) vi, nano等のLinuxのターミナルで動くエディタ
を用いてhome directoryにファイルを作成し、プログラミングを行ったり、TeXのコンパイルを行う(pdfを見るのはEdge等windowsアプリで)ことが出来ます。
Visual Studio Codeという、Windows上で動くエディタがあります。これは、そのWindowsにインストールされたWSLと連携する機能を持っており、なかなか便利です。これをインストールして連携させてみます。
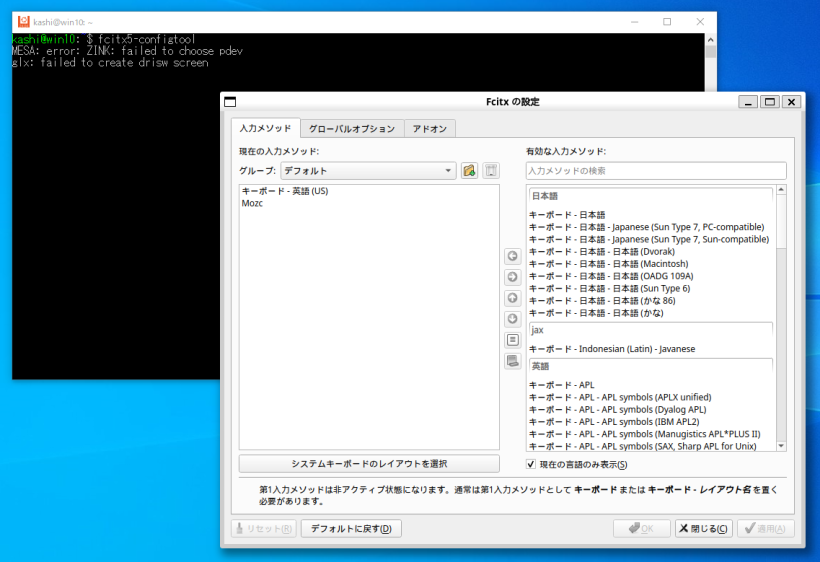
ここから先はあまりお薦めではないかもです。Ubuntuで普段使っているGUIアプリを無理やり動かしてみます。WSLでは、WSLターミナル上ではWindowsのIMEを使って日本語入力が出来ますが、それ以外のGUIアプリケーションで日本語を入力する手段がありません。ここでは、Ubuntuのかな漢字変換システムをインストールして、それを可能にしてみます。
sudo apt install -y fcitx5-mozc
を実行します。次に、home directoryの「.profile」の末尾に、
while true; do
dbus-update-activation-environment --systemd DBUS_SESSION_BUS_ADDRESS DISPLAY XAUTHORITY 2> /dev/null && break
done
export GTK_IM_MODULE=fcitx5
export QT_IM_MODULE=fcitx5
export XMODIFIERS=@im=fcitx5
export INPUT_METHOD=fcitx5
export DefaultIMModule=fcitx5
if [ $SHLVL = 1 ] ; then
(fcitx5 --disable=wayland -d --verbose '*'=0 &)
xset -r 49
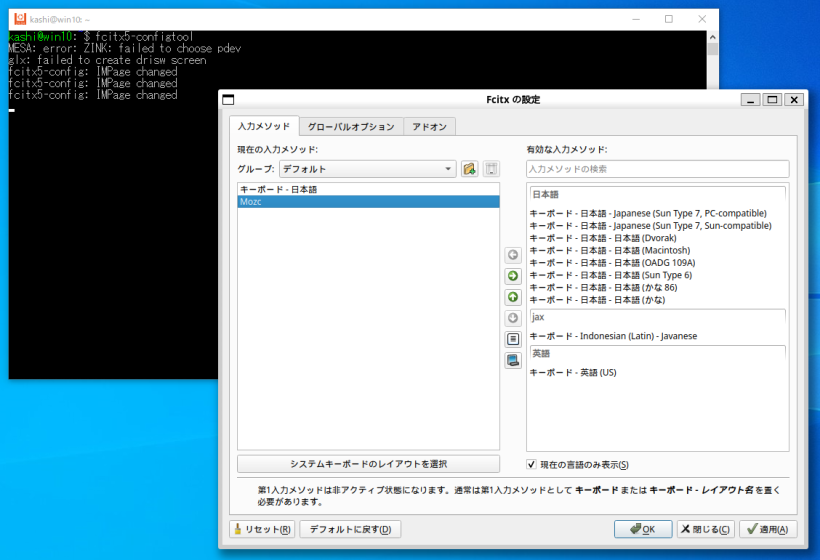
を書き加え、いったんWSLターミナルを閉じて再度起動します。再起動後、WSLターミナルで、「fcitx5-configtool」を起動します。すると、
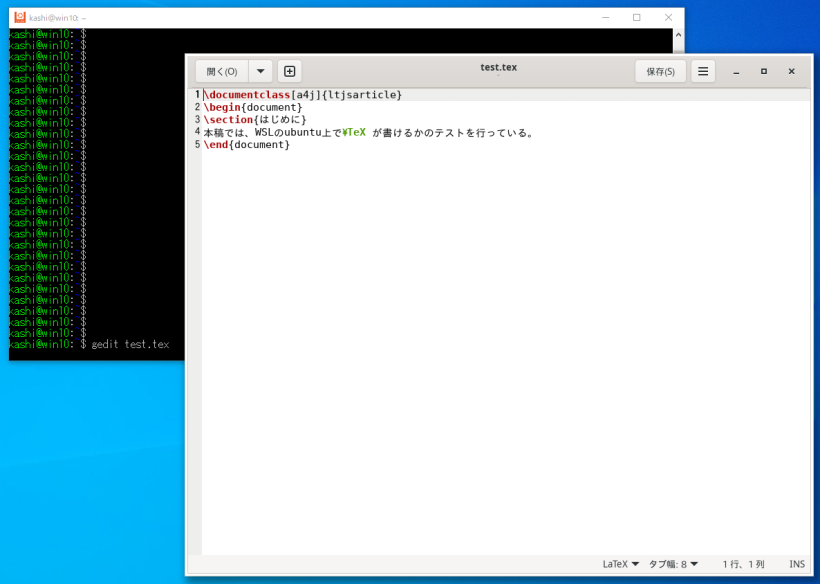
sudo apt install -y gedit
などとして、geditエディタで日本語が書けるのを確認して下さい。
sudo apt install -y x11-apps
sudo apt install -y firefox
sudo apt install -y firefox-locale-ja
sudo apt install -y lxterminal
sudo apt install -y nautilus
sudo apt install -y evince
sudo apt install -y eog
などを入れました。gnome-terminal, gnome-text-editorは少し不安定な感じがしたので、それぞれlxterminal, geditで代用することにしました。
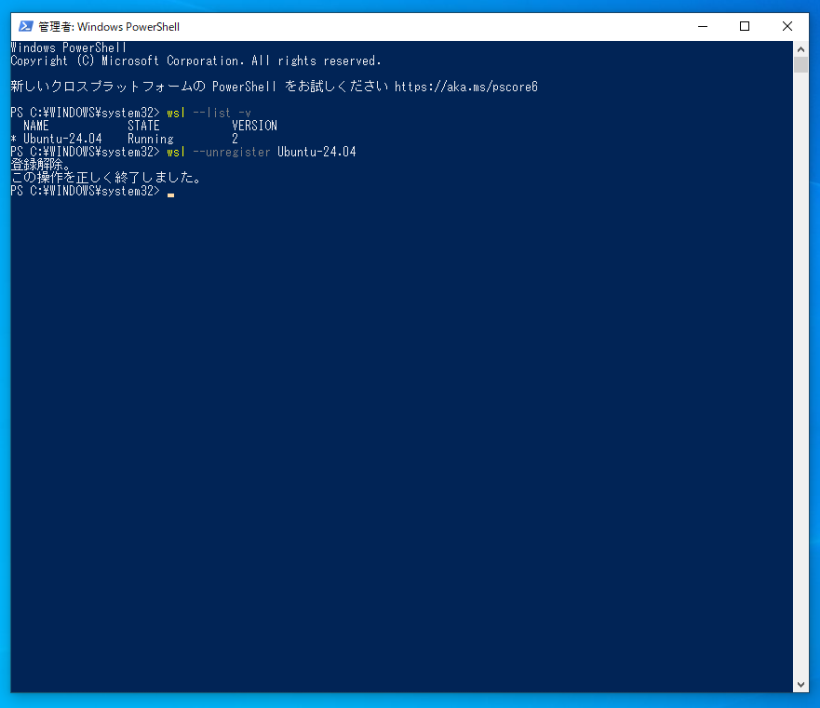
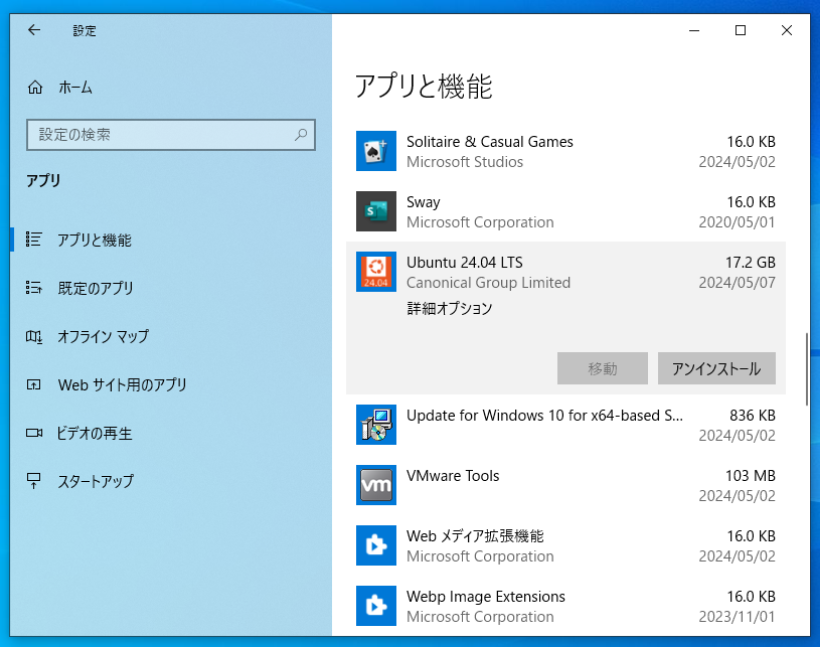
さて、これらのソフトは複雑に連携していて、操作ミスで壊してしまうこともあるかと思います。そこで、きれいさっぱりアンインストールする方法を書いておきます。
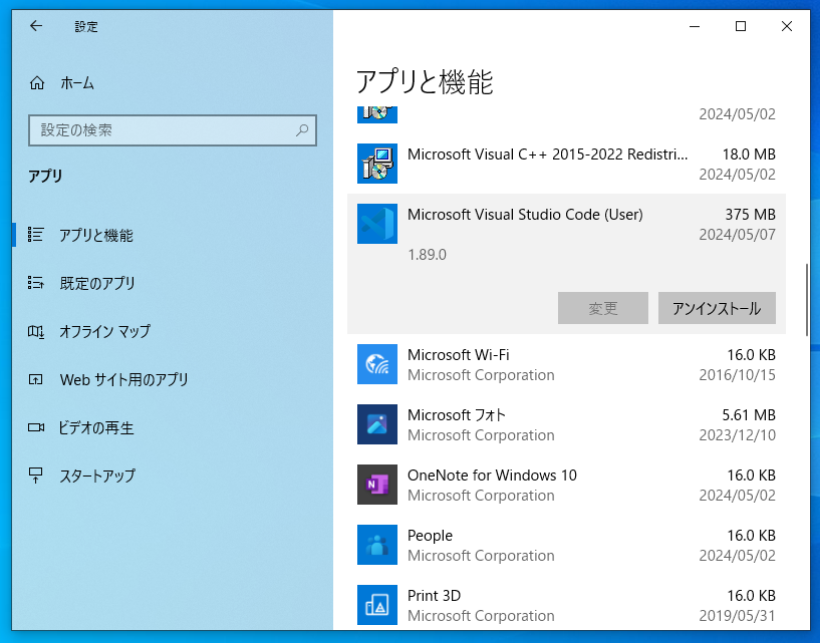
c:\Users\(ユーザ名)\.vscode
c:\Users\(ユーザ名)\AppData\Roaming\Code
の2つのフォルダを削除してください。
お楽しみいただければ幸いです。おかしなところがあればお知らせ下さい。特に無理やりUbuntuのGUIを使うあたりは、いろいろ改善点があると思います。