検索条件

から
検索タグ 精度保証
指定期間 2017年03月の記事
全2件 (1/1ページ)

2017/03/21(火)Henon mapで遊んでみた

精度保証
先週宮古島でINVA2017という研究集会に行ってました。有名なTucker先生をお呼びして講演をしていただいたのですが、Hénon(エノン)mapに関する講演で、面白そうな話だったので講演中いろいろ計算して遊んでいました。

Hénon mapは、
\begin{pmatrix} x_{n+1} \\ y_{n+1} \end{pmatrix} = \begin{pmatrix} 1 + y_n - a x_n^2 \\ b x_n \end{pmatrix}
みたいな漸化式で定義される2次元離散力学系です。a,bの値によってはカオスになることで有名な力学系で、a=1.4、b=0.3がカオスになる有名な値です。その値を使って(x,y)=(0,0)から10000点計算してxy平面にプロットしてみると、

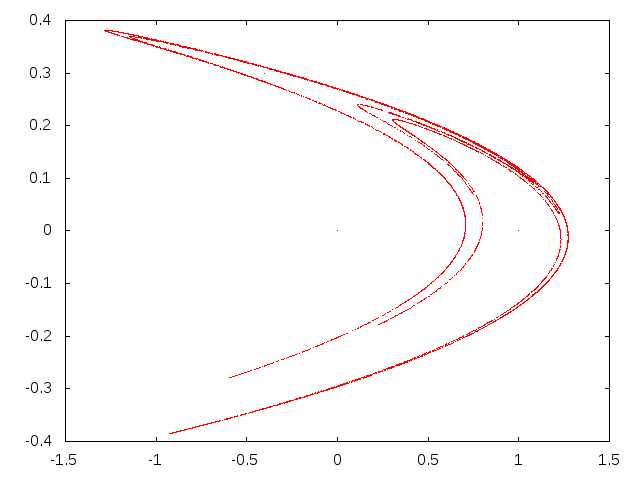
henong.png


のような図形が得られました。

さて、適当な点から出発してn回反復したとき元の点に戻るような軌道をn周期解と言います。周期解には、一度その軌道に入ったらずっとそこから出ない安定な周期解と、わずかな摂動で軌道から外れてしまう不安定な周期解があります。一般にカオスになるときは不安定な周期解しか無いのが普通ですが、よく使われるa=1.4, b=0.3でなく、そこからわずかに値を変化させると安定な周期解が現れることが知られていて、そのような安定な周期解をどうやって探索するか、が講演の内容でした(多分)。

で、とりあえずkvライブラリを使って周期解の探索をしてみよう、というのが以下の内容です。とりあえずa=1.4, b=0.3で、(x,y)の探索範囲は、この論文にあった式
r = \frac{1+|b|+\sqrt{(1+|b|)^2+4a}}{2}
を使って(x,y)\in([-r,r],[-r,r])で探索することにしました。

n回反復する写像の不動点を全解探索するプログラムを素直に書くと、
#include <kv/allsol.hpp>

namespace ub = boost::numeric::ublas;

template <class TT>
struct Henon {
	TT a, b;
	Henon(TT a, TT b) : a(a), b(b) {}
	template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
		ub::vector<T> r(2);

		r(0) = 1 + x(1) - a * x(0) * x(0);
		r(1) = b * x(0);

		return r;
	}
};

template <class F>
struct Repeat_n {
	F f;
	int n;
	Repeat_n(F f, int n): f(f), n(n) {}
	template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
		int i;
		ub::vector<T> tmp;

		tmp = x;
		for (i=0; i<n; i++) tmp = f(tmp);
		return tmp;
	}
};

template <class F>
struct FixedPoint {
	F f;
	FixedPoint(F f): f(f) {}
	template <class T> T operator() (const T& x){
		return f(x) - x;
	}
};

typedef kv::interval<double> itv;

int main()
{
	int i, n;
	ub::vector<itv> x;
	itv a, b;
	itv::base_type r;

	std::cout.precision(17);

	a = "1.4";
	b = "0.3";
	n = 4;

	Henon<itv> f(a, b);
	Repeat_n< Henon<itv> > g(f, n);
	FixedPoint< Repeat_n< Henon<itv> > > h(g);

	r = ((1+abs(b)+sqrt(pow(1+abs(b), 2)+4*a))/2).upper();

	x.resize(2);
	x(0) = itv(-r, r);
	x(1) = itv(-r, r);

	kv::allsol(h, x);
}
のようになりました(henon0.zip)。関数オブジェクトを使っていて、fがHénon写像、gがそれをn回繰り返したもの、hが不動点形式(g(x)-x)です。このプログラムをnを変えながら実行してみます。n=1では、
([-1.1313544770895053,-1.131354477089504],[-0.33940634312685164,-0.33940634312685119])
([0.63135447708950442,0.63135447708950499],[0.18940634312685131,0.18940634312685154])
の2つの1周期解(要するに不動点)が得られました。n=2にすると、
([-0.47580005117505659,-0.47580005117505597],[0.29274001535251664,0.29274001535251721])
([0.97580005117505597,0.97580005117505653],[-0.14274001535251713,-0.14274001535251665])
([0.63135447708950431,0.6313544770895051],[0.18940634312685117,0.18940634312685171])
([-1.1313544770895053,-1.131354477089504],[-0.33940634312685198,-0.33940634312685086])
の4つの解が得られましたが、よく見るとそのうち2つは先程得られた不動点です。更に、残りの2つの解も実質同じ軌道(p→q→pが2周期解ならq→p→qも当然2周期解)なので、2周期解は実質1つだけということが分かります。n=3だと、
([-1.1313544770895053,-1.131354477089504],[-0.33940634312685298,-0.33940634312684986])
([0.6313544770895042,0.63135447708950521],[0.18940634312685095,0.18940634312685187])
が得られますが、これは不動点なので、3周期解は存在しないことが分かりました。n=4の結果を示すと、
([0.63135447708950431,0.6313544770895051],[0.18940634312685045,0.1894063431268524])
([0.63819399262715537,0.63819399262715638],[-0.21203003316582356,-0.2120300331658213])
([-0.70676677721940862,-0.70676677721940761],[0.33752098096070709,0.33752098096070832])
([0.2177617657186289,0.21776176571863363],[0.19145819778814535,0.19145819778814813])
([-0.47580005117505797,-0.47580005117505475],[0.2927400153525157,0.29274001535251815])
([-1.1313544770895064,-1.1313544770895032],[-0.33940634312685631,-0.33940634312684653])
([0.97580005117505508,0.97580005117505731],[-0.14274001535251838,-0.1427400153525154])
([1.1250699365356913,1.1250699365356934],[0.065328529715587863,0.065328529715590903])
と8つの解が得られますが、2つは不動点、2つは2周期解で、4周期解は位相をずらした4つが得られるので実質1つの4周期解があることが分かります。

さて、このように人間の目で選り分けるのは大変なので、より短い周期解の繰り返しや位相がずれただけのものを排除する部分を付け加えて見ました。ついでに、その周期解の安定性をその写像の解のところでのヤコビ行列を計算しその固有値の絶対値の最大値を調べることによって判定する部分も付けてみました。
#include <kv/allsol.hpp>
#include <kv/eig.hpp>

namespace ub = boost::numeric::ublas;

template <class TT>
struct Henon {
	TT a, b;
	Henon(TT a, TT b) : a(a), b(b) {}
	template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
		ub::vector<T> r(2);

		r(0) = 1 + x(1) - a * x(0) * x(0);
		r(1) = b * x(0);

		return r;
	}
};

template <class F>
struct Repeat_n {
	F f;
	int n;
	Repeat_n(F f, int n): f(f), n(n) {}
	template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
		int i;
		ub::vector<T> tmp;

		tmp = x;
		for (i=0; i<n; i++) tmp = f(tmp);
		return tmp;
	}
};

template <class F>
struct FixedPoint {
	F f;
	FixedPoint(F f): f(f) {}
	template <class T> T operator() (const T& x){
		return f(x) - x;
	}
};

typedef kv::interval<double> itv;

int main()
{
	int i, n;
	std::list< ub::vector<itv> > result, result2;
	std::list< ub::vector<itv> >::iterator p, p2;
	ub::vector<itv> x, x2;
	bool flag;
	itv a, b;
	itv::base_type r;

	std::cout.precision(17);

	a = "1.4";
	b = "0.3";
	n = 4;

	Henon<itv> f(a, b);
	Repeat_n< Henon<itv> > g(f, n);
	FixedPoint< Repeat_n< Henon<itv> > > h(g);

	r = ((1+abs(b)+sqrt(pow(1+abs(b), 2)+4*a))/2).upper();

	x.resize(2);
	x(0) = itv(-r, r);
	x(1) = itv(-r, r);

	result = kv::allsol(h, x);

	p = result.begin();
	while (p != result.end()) {
		x = *p;
		flag = true;
		x2 = x;
		for (i=0; i<n-1; i++) {
			x2 = f(x2);
			// check the solution is truly n-pediodic or not
			if (overlap(x, x2)) {
				flag = false;
				break;
			}
			// check the solution is new or not
			p2 = result2.begin();
			while (p2 != result2.end()) {
				if (overlap(*p2, x2)) {
					flag = false;
					break;
				}
				p2++;
			}
			if (flag == false){
				break;
			}
		}

		if (flag) {
			result2.push_back(x);
			std::cout << "true pediodic soluion " << result2.size() << "\n";
			x2 = x;
			for (i=0; i<n; i++) {
				std::cout << x2 << "\n";
				x2 = f(x2);
			}
			std::cout << "\n";

			// calculate maximum eigenvalue of Jacobian
			ub::vector<itv> v1;
			ub::vector< kv::complex<itv> > l;
			itv lm, tmp;
			ub::matrix<itv> m1;
			kv::autodif<itv>::split(g(kv::autodif<itv>::init(x)), v1, m1);
			kv::veig(m1, l);
			std::cout << l << "\n";
			lm = 0;
			for (i=0; i<2; i++) {
				tmp = abs(l(i));
				lm.lower() = std::max(lm.lower(), tmp.lower());
				lm.upper() = std::max(lm.upper(), tmp.upper());
			}
			std::cout << lm << "\n";
			if (lm < 1) {
				std::cout << "stable\n";
			} else if (lm > 1) {
				std::cout << "unstable\n";
			} else {
				std::cout << "stability unknown\n";
			}
		}
		p++;
	}
}
(henon1.zip) これで調べた周期解とその安定性は次のとおりです。
nxy安定性
1[-1.1313544770895053,-1.131354477089504][-0.33940634312685164,-0.33940634312685119]unstable
1[0.63135447708950442,0.63135447708950499][0.18940634312685131,0.18940634312685154]unstable
2[-0.47580005117505659,-0.47580005117505597][0.29274001535251664,0.29274001535251721]unstable
4[0.63819399262715537,0.63819399262715638][-0.21203003316582356,-0.2120300331658213]unstable
6[0.44190995135922078,0.44190995135922451][-0.24126597029523553,-0.24126597029522911]unstable
6[1.0380595354868291,1.0380595354868339][0.093435694641492983,0.093435694641505183]unstable
7[-1.0872860458490461,-1.0872860458490447][0.36967525887581315,0.36967525887581654]unstable
7[-1.0466775735267937,-1.0466775735267894][0.35496793781757529,0.35496793781758157]unstable
7[-0.92617327728451871,-0.92617327728451703][0.34236913808086111,0.3423691380808675]unstable
7[0.81803519601224594,0.81803519601224873][0.15474440787832016,0.15474440787832872]unstable
8[-1.1493133062560075,-1.1493133062560048][0.36560087176430355,0.36560087176431478]unstable
8[-0.8274542278695698,-0.82745422786956712][-0.37646388947765531,-0.37646388947764258]unstable
8[0.90002978920450349,0.90002978920451305][0.13188647717963458,0.13188647717967495]unstable
8[-0.44837319092732131,-0.44837319092731264][-0.34223569372342872,-0.34223569372341905]unstable
8[-0.83680827077054099,-0.83680827077053698][0.35013340845532586,0.35013340845533498]unstable
8[-0.80876720316291007,-0.80876720316289762][0.32983594103956154,0.32983594103958375]unstable
8[0.60111180966072053,0.6011118096607403][-0.21508292460527792,-0.21508292460523506]unstable
n=13まで計算したので、解の数のみ示します。全て不安定解でした。
n周期解の数
12
21
30
41
50
62
74
87
96
1010
1114
1219
1332
全解探索に成功したので、各nに対してこれらで全ての周期解を尽くしていることの数学的証明になっているはずです。

さて、この論文によると、a=1.3866414978735625,b=0.3だと、8周期の安定解が存在するのだそうです。実際、aの値をそれに変えて計算してみると、
nxy安定性
8[0.8742591352635014,0.87425913526350741][0.14575249177868274,0.14575249177870631]unstable
8[-0.84160148826306525,-0.84160148826306058][0.35209093466818297,0.35209093466819364]unstable
8[-0.4853729323948971,-0.48537293239488293][-0.34686239645463785,-0.34686239645462463]unstable
8[0.60580464136231371,0.6058046413623337][-0.21568623282216013,-0.21568623282211638]unstable
8[1.1065521562926103,1.1065521562926253][-0.11533020216315528,-0.11533020216311613]unstable
8[0.42199129139879743,0.42199129139889974][0.1755174868908467,0.17551748689086294]stable
8[0.93092246076173934,0.93092246076183872][0.12609408826805895,0.12609408826806834]unstable
と、6つの不安定解と1つの安定解が得られました。8回繰り返す写像の安定解の場所でのヤコビ行列は、
\begin{pmatrix} [-0.2071075038203655,-0.20710750356848622] & [1.3046842272497074,1.3046842274628959]) \\ [0.046141607262891293,0.046141607302409162] & [-0.29098818813819278,-0.29098818810610671] \end{pmatrix}
で、その固有値の絶対値の最大値は[0.49796393435494867,0.49796393621891983]でした。1より小さいのでこの解は安定なことが分かります。

さて、もう少し遊んでみたりもしたのですが記事も長くなってきたのでこのへんまでにしましょう。力学系方面の知識が無いのでこういう軌道を計算することがどう面白いのかはあまり分からないのですが、いろいろ楽しめました。力学系方面で精度保証付き数値計算をしたいという需要はありそうな気がするので、共同研究なんかに繋がるといいなあ。
コメント（0件）

2017/03/10(金)kv-0.4.41

精度保証
kvライブラリを0.4.41にアップデートしました。

今回の変更は、キャストし忘れでode solverの内部使用型をddとしたときにコンパイル出来なくなっていた修正だけです。

また、ドキュメントにkvライブラリの応用例のページを追加しました。まだ2つだけしか載せていませんが、手元には載せたい応用例がたくさんあるので今後増やしていきたいと思います。また、このページでは数式を表示するプラグインのMathJaxを使ってみました。何か不具合があればお知らせください。
コメント（0件）
OK キャンセル 確認 その他