検索条件
全2件
(1/1ページ)
2017/08/23(水)kv-0.4.42
今回は大きな変更はありません。
- コンパイル時にマクロKV_USE_TPFMAを定義すると、twoproductの計算にfma命令を使うようになる。
- dka.hpp (Durand Kerner Aberth法) の重解時の安定性が向上。
- 精度保証付き数値計算とkvライブラリの概要を説明するスライドを掲載
2017/08/08(火)二重振り子の精度保証付き数値計算
わずかに異なる初期値をもった50本の二重振り子のシミュレーションを動画にしたもので、途中まで完全に重なっているように見える振り子が一気にバラける様子がとても面白い。
次は、それを三重振り子にしたもの。
gmpを用いて高精度計算をしており、ねとらぼで記事にもなりました。
どちらも常微分方程式の計算にはルンゲクッタ法を用いています。わずかな初期値のずれが後に大きな違いをもたらすことがとてもよく分かる動画ですが、一方で、ルンゲクッタ法で計算された値も真値とはわずかにずれており、当然その誤差も同様に後で大きな違いをもたらすことになります。だとすると、果たして意味のある計算になっているのかという疑問が生じます。
そこで、二重振り子の軌道を精度保証付きで計算し、ルンゲクッタ法とどのくらいずれるのか検証してみました。そのtweetがこれです。
このように、4次のルンゲクッタ法(刻み幅2^{-7})と精度保証付き計算とを比較してみると、t=8あたりから先は完全に違う軌道になってしまっていることが分かりました。
以下では、twitterに書けなかった細かい情報を備忘録も兼ねて書いておこうと思います。
使った式は、
\begin{align*}
& (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)
+ m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)
+(m_1+m_2)g \sin \theta_1= 0 \\
& l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2}
-l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0
\end{align*}
のようなものです(Wikipediaの記事と全く同じです)。舞台設定は
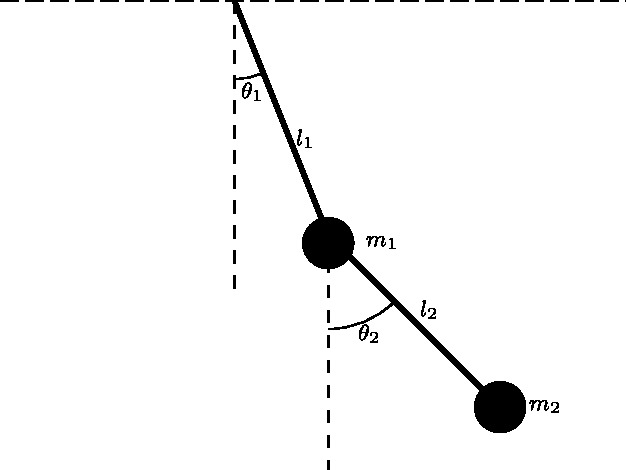
の通り。この式を\ddot{\theta_1}, \ddot{\theta_2}の2変数連立一次方程式と見て解いて正規形に直し、\dot{\theta_1}=\phi_1, \dot{\theta_2}=\phi_2のように置き直して1階4変数の常微分方程式とします。パラメータは
\begin{align*}
m_1 &= m_2 = 1 \\
l_1 &= l_2 = 1 \\
g &= 9.8 \\
\end{align*}
とし、初期値は
\begin{align*}
\theta_1(0) &= \frac{3}{4}\pi \\
\theta_2(0) &= \frac{3}{4}\pi \\
\dot{\theta_1}(0) &= 0 \\
\dot{\theta_2}(0) &= 0
\end{align*}
としました。kvライブラリを用いて、この初期値問題を精度保証付きで計算するプログラムと、4次のルンゲクッタ法で計算するプログラムを書きました。両方のプログラムをzipで上げておきます ( doublependulum.zip )。4次のルンゲクッタ法の刻み幅は固定で2^{-7}としました。精度保証付きの方は全ての時刻の解を多項式の形で連続的に計算しているのですが、ルンゲクッタ法と同じ2^{-7}の刻み幅で密出力させています。この計算結果を動画にしたものが、先のtweetというわけです。
プログラムを走らせて得られた生データを上げておきます ( doublependulum-result.zip )。t=1のときの両プログラムのデータを抜き出すと、
| \theta_1 | \theta_2 | |
|---|---|---|
| kv | [ 0.14046540255551162,0.14046540255558421] | [ -0.71766989300731332,-0.71766989300724726] |
| rk4 | 0.1404652582264235 | -0.71766977132932186 |
このデータをグラフにしてみました。
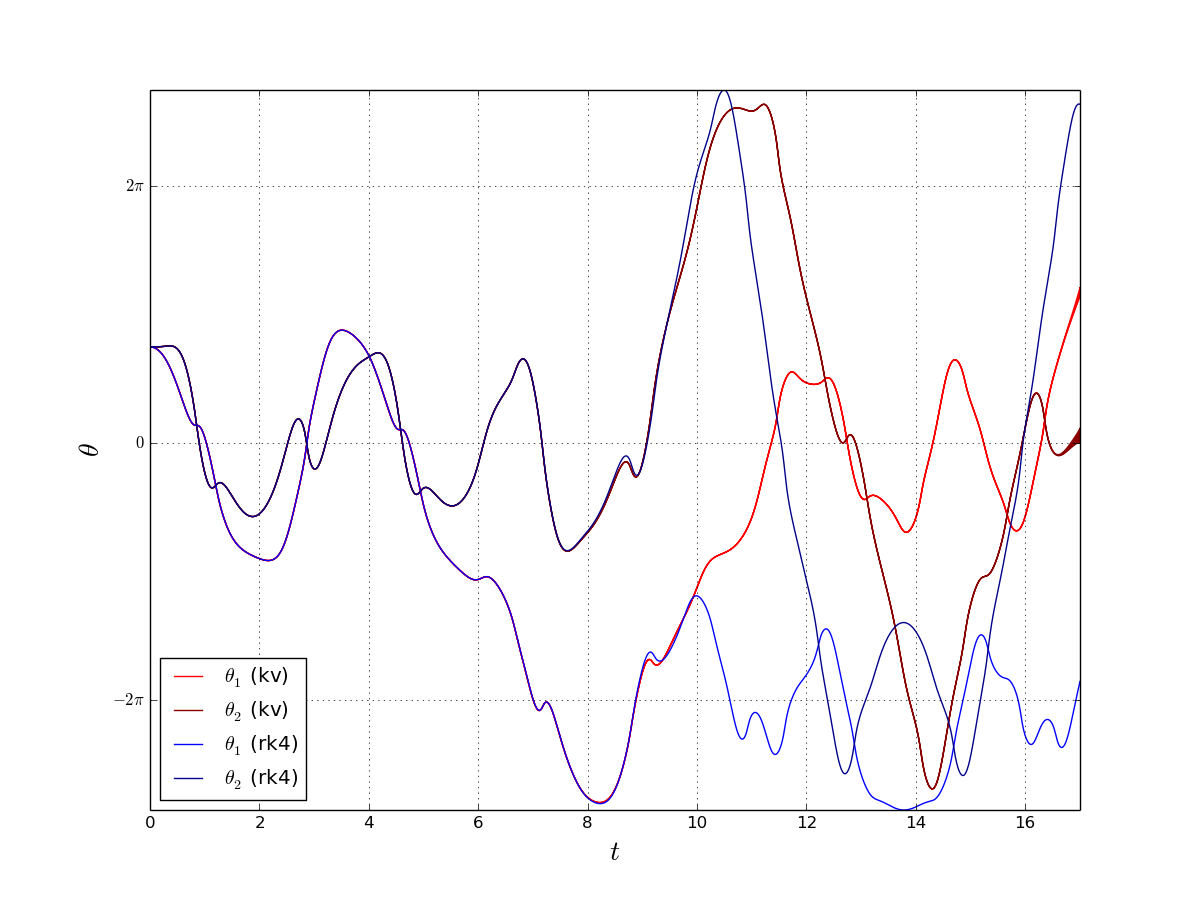
t=8付近でずれが目に見えるようになり、そのあとは完全に異なる軌道を描いています。
精度保証付き計算もいつまでも高精度を保っていられるわけではなく、t=17付近を見るとわずかにグラフに幅があるのが分かります。この後一気に区間幅が爆発し、t=17.05付近で計算不能に陥ります。この精度保証付き計算プログラムはgmpのような高精度数を使用しているわけではなく、内部で使っているのは普通のdoubleです。試しに内部の数値型をdd(擬似4倍精度数)に変えてみたところ、t=30くらいまでは普通に破綻すること無く計算出来ました。
二重振り子の動画を見るだけなら、精度保証してもしなくても動きの「印象」はほとんど変わらないのですが、カオス系に対して数値シミュレーションで何らかの数学的な結論を得ようと思うならば、誤差が明確に把握できる精度保証付き数値計算は必須だと思います。みなさま、精度保証付き数値計算を使いましょう！