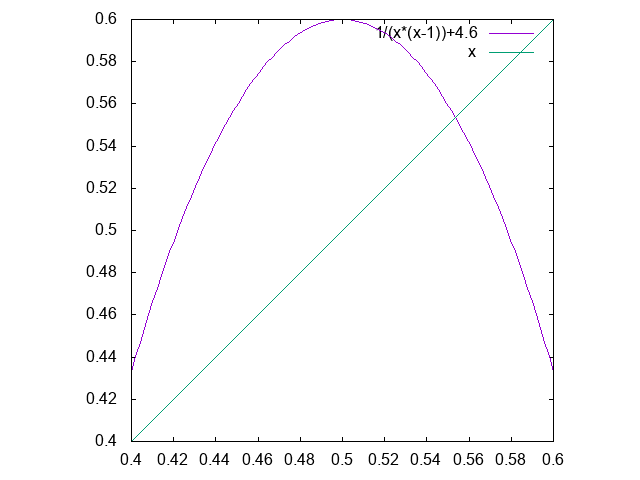
手元のマシンに入っていたいろんな言語で、手当たり次第ベンチマークをしてみました。すべてcore i7 9700、ubuntu 20.04です。すべて普通にaptで入ったバージョンのものを使用しています。なお、計算時間計測は短いものは数回動かして目視で平均的なものを採用、長いものは一発のみ、更にVMwareの中で動かしてるのであまり厳密なものではないことをご承知おきください。
#include <iostream>
int main()
{
int i;
double x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ --version
c++ (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0
Copyright (C) 2019 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
$ c++ -O3 bench.cc
$ time ./a.out
0.487308
real 0m6.065s
user 0m5.964s
sys 0m0.000s
$ clang++ --version
clang version 10.0.0-4ubuntu1
Target: x86_64-pc-linux-gnu
Thread model: posix
InstalledDir: /usr/bin
$ clang++ -O3 bench.cc
$ time ./a.out
0.487308
real 0m5.964s
user 0m5.859s
sys 0m0.008s
class bench {
public static void main(String[] args)
{
int i;
double x;
x = 0.5;
long startTime = System.nanoTime();
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
long endTime = System.nanoTime();
System.out.println(x);
System.out.println((endTime - startTime) / 1000000000.);
}
}
$ java --version
openjdk 11.0.13 2021-10-19
OpenJDK Runtime Environment (build 11.0.13+8-Ubuntu-0ubuntu1.20.04)
OpenJDK 64-Bit Server VM (build 11.0.13+8-Ubuntu-0ubuntu1.20.04, mixed mode, sharing)
$ javac bench.java
$ java bench
0.48730753067792154
5.940579694
fortranのプログラム書いたの人生初なんだが、これでいいのかな。
program bench
implicit none
double precision :: x
integer :: i
x = 0.5d0
do i=1,1000000000
x = 1 / (x * (x - 1)) + 4.6d0
end do
print *, x
end program bench
$ gfortran --version
GNU Fortran (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0
Copyright (C) 2019 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
$ gfortran -O3 bench.f90
$ time ./a.out
0.48730753067792154
real 0m6.154s
user 0m6.045s
sys 0m0.004s
数日前からnimを勉強し始めました。
var x = 0.5
for i in countup(1, 1000000000):
x = 1 / (x * (x-1)) + 4.6
echo(x)
$ nim --version
Nim Compiler Version 1.0.6 [Linux: amd64]
Compiled at 2020-02-27
Copyright (c) 2006-2019 by Andreas Rumpf
active boot switches: -d:release
$ nim c -d:release bench.nim
Hint: used config file '/etc/nim/nim.cfg' [Conf]
Hint: system [Processing]
Hint: widestrs [Processing]
Hint: io [Processing]
Hint: bench [Processing]
CC: stdlib_formatfloat.nim
CC: stdlib_io.nim
CC: stdlib_system.nim
CC: bench.nim
Hint: [Link]
Hint: operation successful (14486 lines compiled; 3.525 sec total; 15.961MiB pea
kmem; Release Build) [SuccessX]
$ time ./bench
0.4873075306779215
real 0m6.029s
user 0m5.912s
sys 0m0.000s
インタプリタだけどJITで爆速なjulia。一回勉強しかけたけど、途中で忙しくなって忘れつつある。
function hoge(x)
for i=1:1000000000
x = 1 / (x * (x-1)) + 4.6
end
return x
end
@time print(hoge(0.5))
$ julia --version
julia version 1.4.1
$ julia bench.jl
0.48730753067792154 6.103540 seconds (500.26 k allocations: 22.774 MiB)
大人気だけど遅いと言われるpython。実際遅い。
import time
def hoge(x, n):
for i in range(n):
x = 1 / (x * (x - 1)) + 4.6;
return x;
s = time.perf_counter()
print(hoge(0.5, 1000000000))
e = time.perf_counter()
print(e - s)
$ python --version
Python 3.8.10
$ python bench.py
0.48730753067792154
75.22909699298907
numbaを使ってJITしてみた。こういう簡単なプログラムだとちゃんと速くなる。
from numba import jit
import time
@jit
def hoge(x, n):
for i in range(n):
x = 1 / (x * (x - 1)) + 4.6;
return x;
s = time.perf_counter()
print(hoge(0.5, 1000000000))
e = time.perf_counter()
print(e - s)
$ python bench2.py
0.48730753067792154
6.189143533993047
$x = 0.5;
for ($i = 0; $i < 1000000000; $i++) {
$x = 1 / ($x * ($x - 1)) + 4.6;
}
print $x;
$ perl --version
This is perl 5, version 30, subversion 0 (v5.30.0) built for x86_64-linux-gnu-thread-multi
(with 50 registered patches, see perl -V for more detail)
Copyright 1987-2019, Larry Wall
Perl may be copied only under the terms of either the Artistic License or the
GNU General Public License, which may be found in the Perl 5 source kit.
Complete documentation for Perl, including FAQ lists, should be found on
this system using "man perl" or "perldoc perl". If you have access to the
Internet, point your browser at http://www.perl.org/, the Perl Home Page.
$ time perl bench.pl
0.487307530677922
real 1m26.594s
user 1m25.330s
sys 0m0.029s
x = 0.5
for i in 1..1000000000
x = 1 / (x * (x - 1)) + 4.6
end
print x, "\n"
$ ruby --version
ruby 2.7.0p0 (2019-12-25 revision 647ee6f091) [x86_64-linux-gnu]
$ time ruby bench.rb
0.48730753067792154
real 1m13.829s
user 1m12.629s
sys 0m0.052s
最小限の仕様でどこまでまともな言語にできるかを追求したような、地味に好きな言語。
x = 0.5
for i=1,1000000000 do
x = 1 / (x * (x - 1)) + 4.6
end
print(x)
$ lua -v
Lua 5.3.3 Copyright (C) 1994-2016 Lua.org, PUC-Rio
$ time lua bench.lua
0.48730753067792
real 0m36.561s
user 0m36.033s
sys 0m0.009s
luaにはluajitという高速実装がある。
$ luajit -v
LuaJIT 2.1.0-beta3 -- Copyright (C) 2005-2017 Mike Pall. http://luajit.org/
$ time luajit bench.lua
0.48730753067792
real 0m5.958s
user 0m5.863s
sys 0m0.001s
BEGIN {
x = 0.5;
for (i=1; i<=1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
print x;
}
$ awk --version
GNU Awk 5.0.1, API: 2.0 (GNU MPFR 4.0.2, GNU MP 6.2.0)
Copyright (C) 1989, 1991-2019 Free Software Foundation.
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 3 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see http://www.gnu.org/licenses/.
$ time awk -f bench.awk
0.487308
real 1m37.501s
user 1m35.837s
sys 0m0.095s
<?php
$x = 0.5;
for ($i=1; $i<=1000000000; $i++) {
$x = 1/($x * ($x - 1)) + 4.6;
}
echo $x, "\n";
?>
$ php --version
PHP 7.4.3 (cli) (built: Oct 25 2021 18:20:54) ( NTS )
Copyright (c) The PHP Group
Zend Engine v3.4.0, Copyright (c) Zend Technologies
with Zend OPcache v7.4.3, Copyright (c), by Zend Technologies
$ time php bench.php
0.48730753067792
real 0m16.971s
user 0m16.491s
sys 0m0.048s
いくらなんでも遅すぎ?
1;
function x = hoge(x)
for i=1:1000000000
x = 1 / (x*(x-1)) +4.6;
end
end
tic; x = hoge(0.5); toc
x
$ octave --version
GNU Octave, version 5.2.0
Copyright (C) 2020 John W. Eaton and others.
This is free software; see the source code for copying conditions.
There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE.
Octave was configured for "x86_64-pc-linux-gnu".
Additional information about Octave is available at https://www.octave.org.
Please contribute if you find this software useful.
For more information, visit https://www.octave.org/get-involved.html
Read https://www.octave.org/bugs.html to learn how to submit bug reports.
$ octave bench.m
Elapsed time is 1434.74 seconds.
x = 0.48731
- IEEE754には従っているようで、試したすべての言語で同じ結果が得られた。
- コンパイラ言語、もしくはJITありのインタプリタは大体6秒前後。
- JITなしのインタプリタは千差万別。地味にphpが速い、次にlua、有名インタプリタ勢は大体1分強。octaveはなにかおかしい。
| 言語 | 計算時間(秒) |
|---|
| C++(gcc) | 5.964 |
| C++(clang) | 5.859 |
| Java | 5.941 |
| fortran | 6.045 |
| nim | 5.912 |
| julia | 6.103 |
| python | 75.23 |
| python+numba | 6.189 |
| perl | 85.33 |
| ruby | 72.63 |
| lua | 36.03 |
| luajit | 5.863 |
| awk | 95.84 |
| php | 16.49 |
| octave | 1435 |
今度は言語はC++(gcc)に固定し、計算精度を倍精度(double)から他のものに変えて計算時間を測ってみます。むしろこっちに興味がある人もいることでしょう。
倍精度と変わらないかとも思いましたが、少し速くなるようです。
#include <iostream>
int main()
{
int i;
float x;
x = 0.5f; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1.0f / (x * (x - 1.0f)) + 4.6f;
}
std::cout << x << std::endl;
}
$ c++ -O3 float32.cc
$ time ./a.out
0.596567
real 0m5.460s
user 0m5.371s
sys 0m0.004s
SSE等のSIMD命令が出てくる前のIntel CPUで主に使われていたFPUの演算器は、全長80bit、仮数部64bitの拡張倍精度を持っています。今どきのx86_64向けのバイナリーではFPUを使うことはなく、盲腸のような存在ですが、頑張って使おうと思えば使うことが出来ます。ただし、今のMSVCでは使うのは難しいです。詳細は省きますが、gccやclangでは使うことができて、math.hまたはcmathをincludeした上で_Float64xという型名で使うのが一番良さそうです。
#include <iostream>
#include <cmath>
int main()
{
int i;
_Float64x x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float64x.cc
$ time ./a.out
0.447779
real 0m6.436s
user 0m6.325s
sys 0m0.008s
この並列性が生かせない特殊なベンチマークのためだとは思いますが、倍精度と遜色ない速度が出ているのは少し驚きです。
倍精度浮動小数点数を2つ使って、擬似的に106bit相当の仮数部を持つ4倍精度数を作る方法があります。double-doubleとか、縮めてddとか呼ばれます。Baileyによるqdライブラリがよく知られています。qdは、倍精度を4つ使うquad-doubleと2つ使うdouble-doubleの演算ができますが、今回はdouble-doubleの方を試してみました。sudo apt install qd-devでインストールしたものを使いました。
#include <iostream>
#include <qd/qd_real.h>
int main()
{
unsigned int oldcw;
fpu_fix_start(&oldcw);
int i;
dd_real x;
x = 0.5;
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << "\n";
fpu_fix_end(&oldcw);
}
$ c++ -O3 qd.cc -lqd
$ time ./a.out
5.343242e-01
real 0m48.568s
user 0m48.047s
sys 0m0.008s
私が作っている精度保証付き数値計算のためのライブラリkvにも、double-double数が実装されているので、その計算時間も計測してみました。
#include <kv/dd.hpp>
int main()
{
int i;
kv::dd x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 dd.cc
$ time ./a.out
0.599108
real 0m37.365s
user 0m36.737s
sys 0m0.012s
$ c++ -O3 -DKV_USE_TPFMA dd.cc
$ time ./a.out
0.599108
real 0m30.161s
user 0m29.656s
sys 0m0.009s
FMA非使用とFMA使用の両方でコンパイルしてみました。どちらでもqdより速いのは意外だったけど、嬉しいですね!
IEEE754-2008で規格化された、全長128bit、仮数部113bitの浮動小数点形式です。残念ながらハードウェアでサポートしているCPUはほとんどありません。gccではlibquadmathで実装されたソフトウェアエミュレーションを使うことができます。cout等を使って楽をしたかったので、このサンプルではboost::multiprecisionを通じて使用しています。
#include <iostream>
#include <boost/multiprecision/float128.hpp>
int main()
{
int i;
boost::multiprecision::float128 x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float128.cc -lquadmath
$ time ./a.out
0.547514
real 1m41.450s
user 1m39.683s
sys 0m0.028s
ソフトウェアエミュレーションにしては速い印象です。よほどすごい人が書いたのでしょうか。
mpfrは有名なライブラリで、任意の仮数部長の浮動小数点演算を行うことができます。kvライブラリのmpfrラッパー機能を使って、53bit, 64bit, 106bit, 113bitの浮動小数点演算の速度を計測してみました。mpfrは、sudo apt install mpfr-devで入れたものです。
#include <kv/mpfr.hpp>
int main()
{
int i;
kv::mpfr<53> x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
このプログラム中の53の部分を変えながら計測してみました。
$ c++ -O3 mpfr53.cc -lmpfr
$ time ./a.out
0.487308
real 3m54.608s
user 3m50.821s
sys 0m0.044s
$ c++ -O3 mpfr64.cc -lmpfr
$ time ./a.out
0.447779
real 5m16.806s
user 5m11.236s
sys 0m0.111s
$ c++ -O3 mpfr106.cc -lmpfr
$ time ./a.out
0.576081
real 5m37.827s
user 5m32.035s
sys 0m0.111s
$ c++ -O3 mpfr113.cc -lmpfr
$ time ./a.out
0.547514
real 5m42.499s
user 5m36.300s
sys 0m0.241s
mpfrは、多倍長演算のプログラムとしては十分高速で定評がありますが、さすがに遅いですね。
| 数値型 | 計算時間(秒) |
|---|
| 単精度 (全長32bit, 仮数部24bit) | 5.371 |
| 倍精度 (全長64bit, 仮数部53bit) | 5.964 |
| Intel拡張倍精度 (全長80bit, 仮数部64bit) | 6.325 |
| double-double by qd (全長128bit, 仮数部106bit相当) | 48.05 |
| double-double by kv (全長128bit, 仮数部106bit相当) | 36.74 |
| double-double by kv with FMA (全長128bit, 仮数部106bit相当) | 29.66 |
| float128 (全長128bit, 仮数部113bit) | 99.68 |
| mpfr (仮数部53bit) | 230.8 |
| mpfr (仮数部64bit) | 311.2 |
| mpfr (仮数部106bit) | 332.0 |
| mpfr (仮数部113bit) | 336.3 |