2021/12/23(木)変なベンチマークテスト
変なベンチマーク?
元々のきっかけは、のツイートでした。加減乗除が一回ずつ出てきて、発散やゼロ除算を起こさず無限に回れるループが面白いなと思いました。核心部は、
a = 123;
for (j = 0; j< 1000000000; j++) {
a = (a * a - a) / (a + a);
}
の部分です。確かに加減乗除を一回ずつ含んでいる。約分すると
a = (a - 1) /2
というループで、a=-1に収束します。ただ、初期値を-1にしたら最適化コンパイラに(ずっと-1であることを)見抜かれてしまってループを消されてしまったりしました。これに触発されて、値が一定でなく乱数のように振る舞い、最適化に消されず計算せざるを得ないような計算式はできないかなと考えてみました。
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
初期値は0.4から0.6の間の適当な値にします。すると、0.4から0.6の間を乱数のように振る舞います。元の式は分母(a*a-a)と分子(a+a)が独立に計算できるのである種の並列性を活かすことができましたが、こちらは前の計算の結果が出てこないと次の計算が始められないような構造になっています。また、元の式はa*a-aの部分をFMAを使って計算して高速化できる可能性がありますが、こちらはFMAの使える箇所がありません。つまり、最新のCPUに備わっている高速化機構を拒否するような計算になっているので、純粋な(?)計算速度を計測できると思われます。このつぶやきに続けていくつかベンチマークを流しましたが、使ったプログラムや条件等、きちんと書き残しておこうと思って書いているのが、この記事です。
いろんな言語でベンチマーク
手元のマシンに入っていたいろんな言語で、手当たり次第ベンチマークをしてみました。すべてcore i7 9700、ubuntu 20.04です。すべて普通にaptで入ったバージョンのものを使用しています。なお、計算時間計測は短いものは数回動かして目視で平均的なものを採用、長いものは一発のみ、更にVMwareの中で動かしてるのであまり厳密なものではないことをご承知おきください。C++ (gcc)
#include <iostream>
int main()
{
int i;
double x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ --version c++ (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0 Copyright (C) 2019 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. $ c++ -O3 bench.cc $ time ./a.out 0.487308 real 0m6.065s user 0m5.964s sys 0m0.000s
C++ (clang)
$ clang++ --version clang version 10.0.0-4ubuntu1 Target: x86_64-pc-linux-gnu Thread model: posix InstalledDir: /usr/bin $ clang++ -O3 bench.cc $ time ./a.out 0.487308 real 0m5.964s user 0m5.859s sys 0m0.008s
Java
class bench {
public static void main(String[] args)
{
int i;
double x;
x = 0.5;
long startTime = System.nanoTime();
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
long endTime = System.nanoTime();
System.out.println(x);
System.out.println((endTime - startTime) / 1000000000.);
}
}
$ java --version openjdk 11.0.13 2021-10-19 OpenJDK Runtime Environment (build 11.0.13+8-Ubuntu-0ubuntu1.20.04) OpenJDK 64-Bit Server VM (build 11.0.13+8-Ubuntu-0ubuntu1.20.04, mixed mode, sharing) $ javac bench.java $ java bench 0.48730753067792154 5.940579694
fortran
fortranのプログラム書いたの人生初なんだが、これでいいのかな。program bench implicit none double precision :: x integer :: i x = 0.5d0 do i=1,1000000000 x = 1 / (x * (x - 1)) + 4.6d0 end do print *, x end program bench
$ gfortran --version GNU Fortran (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0 Copyright (C) 2019 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. $ gfortran -O3 bench.f90 $ time ./a.out 0.48730753067792154 real 0m6.154s user 0m6.045s sys 0m0.004s
nim
数日前からnimを勉強し始めました。var x = 0.5 for i in countup(1, 1000000000): x = 1 / (x * (x-1)) + 4.6 echo(x)
$ nim --version Nim Compiler Version 1.0.6 [Linux: amd64] Compiled at 2020-02-27 Copyright (c) 2006-2019 by Andreas Rumpf active boot switches: -d:release $ nim c -d:release bench.nim Hint: used config file '/etc/nim/nim.cfg' [Conf] Hint: system [Processing] Hint: widestrs [Processing] Hint: io [Processing] Hint: bench [Processing] CC: stdlib_formatfloat.nim CC: stdlib_io.nim CC: stdlib_system.nim CC: bench.nim Hint: [Link] Hint: operation successful (14486 lines compiled; 3.525 sec total; 15.961MiB pea kmem; Release Build) [SuccessX] $ time ./bench 0.4873075306779215 real 0m6.029s user 0m5.912s sys 0m0.000s
julia
インタプリタだけどJITで爆速なjulia。一回勉強しかけたけど、途中で忙しくなって忘れつつある。
function hoge(x)
for i=1:1000000000
x = 1 / (x * (x-1)) + 4.6
end
return x
end
@time print(hoge(0.5))
$ julia --version julia version 1.4.1 $ julia bench.jl 0.48730753067792154 6.103540 seconds (500.26 k allocations: 22.774 MiB)
python
大人気だけど遅いと言われるpython。実際遅い。import time def hoge(x, n): for i in range(n): x = 1 / (x * (x - 1)) + 4.6; return x; s = time.perf_counter() print(hoge(0.5, 1000000000)) e = time.perf_counter() print(e - s)
$ python --version Python 3.8.10 $ python bench.py 0.48730753067792154 75.22909699298907
python + numba
numbaを使ってJITしてみた。こういう簡単なプログラムだとちゃんと速くなる。from numba import jit import time @jit def hoge(x, n): for i in range(n): x = 1 / (x * (x - 1)) + 4.6; return x; s = time.perf_counter() print(hoge(0.5, 1000000000)) e = time.perf_counter() print(e - s)
$ python bench2.py 0.48730753067792154 6.189143533993047
perl
$x = 0.5;
for ($i = 0; $i < 1000000000; $i++) {
$x = 1 / ($x * ($x - 1)) + 4.6;
}
print $x;
$ perl --version This is perl 5, version 30, subversion 0 (v5.30.0) built for x86_64-linux-gnu-thread-multi (with 50 registered patches, see perl -V for more detail) Copyright 1987-2019, Larry Wall Perl may be copied only under the terms of either the Artistic License or the GNU General Public License, which may be found in the Perl 5 source kit. Complete documentation for Perl, including FAQ lists, should be found on this system using "man perl" or "perldoc perl". If you have access to the Internet, point your browser at http://www.perl.org/, the Perl Home Page. $ time perl bench.pl 0.487307530677922 real 1m26.594s user 1m25.330s sys 0m0.029s
ruby
x = 0.5 for i in 1..1000000000 x = 1 / (x * (x - 1)) + 4.6 end print x, "\n"
$ ruby --version ruby 2.7.0p0 (2019-12-25 revision 647ee6f091) [x86_64-linux-gnu] $ time ruby bench.rb 0.48730753067792154 real 1m13.829s user 1m12.629s sys 0m0.052s
lua
最小限の仕様でどこまでまともな言語にできるかを追求したような、地味に好きな言語。
x = 0.5
for i=1,1000000000 do
x = 1 / (x * (x - 1)) + 4.6
end
print(x)
$ lua -v Lua 5.3.3 Copyright (C) 1994-2016 Lua.org, PUC-Rio $ time lua bench.lua 0.48730753067792 real 0m36.561s user 0m36.033s sys 0m0.009s
luajit
luaにはluajitという高速実装がある。$ luajit -v LuaJIT 2.1.0-beta3 -- Copyright (C) 2005-2017 Mike Pall. http://luajit.org/ $ time luajit bench.lua 0.48730753067792 real 0m5.958s user 0m5.863s sys 0m0.001s
awk
BEGIN {
x = 0.5;
for (i=1; i<=1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
print x;
}
$ awk --version GNU Awk 5.0.1, API: 2.0 (GNU MPFR 4.0.2, GNU MP 6.2.0) Copyright (C) 1989, 1991-2019 Free Software Foundation. This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/. $ time awk -f bench.awk 0.487308 real 1m37.501s user 1m35.837s sys 0m0.095s
php
<?php
$x = 0.5;
for ($i=1; $i<=1000000000; $i++) {
$x = 1/($x * ($x - 1)) + 4.6;
}
echo $x, "\n";
?>
$ php --version
PHP 7.4.3 (cli) (built: Oct 25 2021 18:20:54) ( NTS )
Copyright (c) The PHP Group
Zend Engine v3.4.0, Copyright (c) Zend Technologies
with Zend OPcache v7.4.3, Copyright (c), by Zend Technologies
$ time php bench.php
0.48730753067792
real 0m16.971s
user 0m16.491s
sys 0m0.048s
octave
いくらなんでも遅すぎ?1; function x = hoge(x) for i=1:1000000000 x = 1 / (x*(x-1)) +4.6; end end tic; x = hoge(0.5); toc x
$ octave --version GNU Octave, version 5.2.0 Copyright (C) 2020 John W. Eaton and others. This is free software; see the source code for copying conditions. There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. Octave was configured for "x86_64-pc-linux-gnu". Additional information about Octave is available at https://www.octave.org. Please contribute if you find this software useful. For more information, visit https://www.octave.org/get-involved.html Read https://www.octave.org/bugs.html to learn how to submit bug reports. $ octave bench.m Elapsed time is 1434.74 seconds. x = 0.48731
いろんな言語でベンチマークまとめ
- IEEE754には従っているようで、試したすべての言語で同じ結果が得られた。
- コンパイラ言語、もしくはJITありのインタプリタは大体6秒前後。
- JITなしのインタプリタは千差万別。地味にphpが速い、次にlua、有名インタプリタ勢は大体1分強。octaveはなにかおかしい。
| 言語 | 計算時間(秒) |
|---|---|
| C++(gcc) | 5.964 |
| C++(clang) | 5.859 |
| Java | 5.941 |
| fortran | 6.045 |
| nim | 5.912 |
| julia | 6.103 |
| python | 75.23 |
| python+numba | 6.189 |
| perl | 85.33 |
| ruby | 72.63 |
| lua | 36.03 |
| luajit | 5.863 |
| awk | 95.84 |
| php | 16.49 |
| octave | 1435 |
倍精度以外で計算させてみる
今度は言語はC++(gcc)に固定し、計算精度を倍精度(double)から他のものに変えて計算時間を測ってみます。むしろこっちに興味がある人もいることでしょう。単精度(float)
倍精度と変わらないかとも思いましたが、少し速くなるようです。
#include <iostream>
int main()
{
int i;
float x;
x = 0.5f; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1.0f / (x * (x - 1.0f)) + 4.6f;
}
std::cout << x << std::endl;
}
$ c++ -O3 float32.cc $ time ./a.out 0.596567 real 0m5.460s user 0m5.371s sys 0m0.004s
Intelの80bit拡張倍精度
SSE等のSIMD命令が出てくる前のIntel CPUで主に使われていたFPUの演算器は、全長80bit、仮数部64bitの拡張倍精度を持っています。今どきのx86_64向けのバイナリーではFPUを使うことはなく、盲腸のような存在ですが、頑張って使おうと思えば使うことが出来ます。ただし、今のMSVCでは使うのは難しいです。詳細は省きますが、gccやclangでは使うことができて、math.hまたはcmathをincludeした上で_Float64xという型名で使うのが一番良さそうです。
#include <iostream>
#include <cmath>
int main()
{
int i;
_Float64x x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float64x.cc $ time ./a.out 0.447779 real 0m6.436s user 0m6.325s sys 0m0.008sこの並列性が生かせない特殊なベンチマークのためだとは思いますが、倍精度と遜色ない速度が出ているのは少し驚きです。
double-double (qdライブラリ)
倍精度浮動小数点数を2つ使って、擬似的に106bit相当の仮数部を持つ4倍精度数を作る方法があります。double-doubleとか、縮めてddとか呼ばれます。Baileyによるqdライブラリがよく知られています。qdは、倍精度を4つ使うquad-doubleと2つ使うdouble-doubleの演算ができますが、今回はdouble-doubleの方を試してみました。sudo apt install qd-devでインストールしたものを使いました。
#include <iostream>
#include <qd/qd_real.h>
int main()
{
unsigned int oldcw;
fpu_fix_start(&oldcw);
int i;
dd_real x;
x = 0.5;
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << "\n";
fpu_fix_end(&oldcw);
}
$ c++ -O3 qd.cc -lqd $ time ./a.out 5.343242e-01 real 0m48.568s user 0m48.047s sys 0m0.008s
double-double (kvライブラリ)
私が作っている精度保証付き数値計算のためのライブラリkvにも、double-double数が実装されているので、その計算時間も計測してみました。
#include <kv/dd.hpp>
int main()
{
int i;
kv::dd x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 dd.cc $ time ./a.out 0.599108 real 0m37.365s user 0m36.737s sys 0m0.012s $ c++ -O3 -DKV_USE_TPFMA dd.cc $ time ./a.out 0.599108 real 0m30.161s user 0m29.656s sys 0m0.009sFMA非使用とFMA使用の両方でコンパイルしてみました。どちらでもqdより速いのは意外だったけど、嬉しいですね!
float128
IEEE754-2008で規格化された、全長128bit、仮数部113bitの浮動小数点形式です。残念ながらハードウェアでサポートしているCPUはほとんどありません。gccではlibquadmathで実装されたソフトウェアエミュレーションを使うことができます。cout等を使って楽をしたかったので、このサンプルではboost::multiprecisionを通じて使用しています。
#include <iostream>
#include <boost/multiprecision/float128.hpp>
int main()
{
int i;
boost::multiprecision::float128 x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float128.cc -lquadmath $ time ./a.out 0.547514 real 1m41.450s user 1m39.683s sys 0m0.028sソフトウェアエミュレーションにしては速い印象です。よほどすごい人が書いたのでしょうか。
mpfr
mpfrは有名なライブラリで、任意の仮数部長の浮動小数点演算を行うことができます。kvライブラリのmpfrラッパー機能を使って、53bit, 64bit, 106bit, 113bitの浮動小数点演算の速度を計測してみました。mpfrは、sudo apt install mpfr-devで入れたものです。
#include <kv/mpfr.hpp>
int main()
{
int i;
kv::mpfr<53> x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
このプログラム中の53の部分を変えながら計測してみました。$ c++ -O3 mpfr53.cc -lmpfr $ time ./a.out 0.487308 real 3m54.608s user 3m50.821s sys 0m0.044s $ c++ -O3 mpfr64.cc -lmpfr $ time ./a.out 0.447779 real 5m16.806s user 5m11.236s sys 0m0.111s $ c++ -O3 mpfr106.cc -lmpfr $ time ./a.out 0.576081 real 5m37.827s user 5m32.035s sys 0m0.111s $ c++ -O3 mpfr113.cc -lmpfr $ time ./a.out 0.547514 real 5m42.499s user 5m36.300s sys 0m0.241smpfrは、多倍長演算のプログラムとしては十分高速で定評がありますが、さすがに遅いですね。
倍精度以外の計算速度まとめ
| 数値型 | 計算時間(秒) |
|---|---|
| 単精度 (全長32bit, 仮数部24bit) | 5.371 |
| 倍精度 (全長64bit, 仮数部53bit) | 5.964 |
| Intel拡張倍精度 (全長80bit, 仮数部64bit) | 6.325 |
| double-double by qd (全長128bit, 仮数部106bit相当) | 48.05 |
| double-double by kv (全長128bit, 仮数部106bit相当) | 36.74 |
| double-double by kv with FMA (全長128bit, 仮数部106bit相当) | 29.66 |
| float128 (全長128bit, 仮数部113bit) | 99.68 |
| mpfr (仮数部53bit) | 230.8 |
| mpfr (仮数部64bit) | 311.2 |
| mpfr (仮数部106bit) | 332.0 |
| mpfr (仮数部113bit) | 336.3 |
変なベンチマークの力学系的性質
ここからはオマケです。一応、この反復式
x_{n+1} = \frac{1}{x_n(x_n-1)} + 4.6
をどうやって作ったのか種明かしをしておきましょう。区間[0.4,0.6]でこの右辺のグラフを書くと、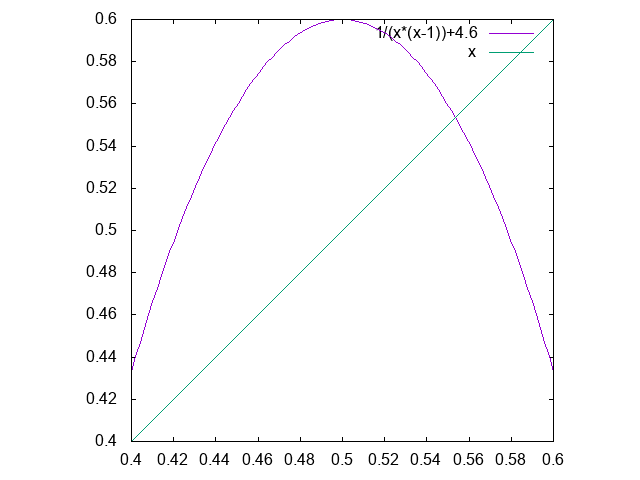
のようになります。すなわち、区間[0.4,0.6]から区間[0.4,0.6]への写像で、いわゆるロジスティック写像に形を似せて、カオスの発生を期待しました。
これが本当にカオスになっているのか自分の知識ではよく分かりませんが、安定な不動点、あるいは安定なn周期点があるとそこに吸い込まれてしまうので、それらが不安定である必要があります。不動点~5周期点までを探索してその安定性を調べてみたら、
| 周期点 | 傾き |
|---|---|
| 不動点 | |
| [0.55356306259771814,0.55356306259771904] | [-1.7540458821004337,-1.7540458821003905] |
| 2周期点 | |
| [0.47251229982482656,0.47251229982483978] | [-2.6496000000100227,-2.6495999999899826] |
| [0.58787417360511429,0.58787417360512307] | [-2.649600000013118,-2.6495999999869042] |
| 4周期点 | |
| [0.45660292682622499,0.45660292682782184] | [-6.994344006430338,-6.9943413287099849] |
| [0.56963838378845921,0.56963838379004439] | [-6.9943442880413019,-6.994341047098123] |
| [0.52087302149875114,0.52087302149987225] | [-6.9943435009524846,-6.9943418341871632] |
| [0.59301690190605937,0.59301690190710344] | [-6.9943446375696477,-6.9943406975699096] |
| 5周期点1 | |
| [0.49241639587271796,0.49241639589626041] | [-5.3195999647673152,-5.3191146240917346] |
| [0.59907961143524002,0.59907961146046785] | [-5.3210234368141052,-5.3176911750450219] |
| [0.43651199326412942,0.43651199328730845] | [-5.319869439031236,-5.3188451535460181] |
| [0.53445153616664387,0.5344515362008826] | [-5.3198513032572504,-5.3188632923945835] |
| [0.58091887627954896,0.58091887630723616] | [-5.3198877237365352,-5.3188268706445134] |
| 5周期点2 | |
| [0.43930700020768825,0.4393070002409904] | [7.3230674094215144,7.3246535122595358] |
| [0.54018034001802039,0.54018034004123794] | [7.3234484071188221,7.3242725048956273] |
| [0.57400074538735523,0.57400074542057201] | [7.3231434952559464,7.3245774251428078] |
| [0.51042003579714645,0.51042003582068152] | [7.3235356733528114,7.3241852373848194] |
| [0.59826201082553276,0.59826201084694897] | [7.3224303075700802,7.3252906173775747] |
2021/11/30(火)NVR2021
今回で5回めで、コロナ禍で昨年に引き続き残念ながらオンラインです。今年は、大石CRESTが最終年度で成果報告会を開催してほしいという要請があり、時期も近くて参加メンバーも多くが被るので、共同開催することにしました。CREST報告会が土曜日、NVRが日曜日でした。いろいろ重なって大変でしたが、無事終わってホッとしています。
使用したスライドを張っておきます。1つ目はdouble-doubleに関する話題、2つ目はKrawczyk法の候補者集合に関する話題です。2つ目は軽い話題で発表時間も短め(20分)です。
2021/11/12(金)kv-0.4.53
今回は2つのbug-fixです。
1つ目は、非常に特殊な条件ですが、xがdouble-double数で、その上端が(DBL_MAX+正数)というoverflow寸前の巨大数だった場合に、sqrt(x)の計算結果の幅が広くなってしまう(double-doubleとしてふさわしい精度が出ずにdouble程度の区間幅になってしまう)というバグの修正です。実際、
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
int main(){
kv::interval<kv::dd> x;
std::cout.precision(34);
x = std::numeric_limits<kv::dd>::max();
std::cout << x << "\n";
std::cout << sqrt(x) << "\n";
}
を実行すると、[1.340780792994259561100831764080293e+154,1.340780792994259672743259815885529e+154]と計算されてしまっていました。修正後は、
[1.340780792994259672743259815885478e+154,1.340780792994259672743259815885529e+154]ときちんと計算されるようになりました。中田真秀先生の、
のtweetで気づくことができました(kvではなくQDライブラリへの言及ではありますが)。中田先生ありがとうございました。
2つめは、自動step幅調節機能付き定積分を行う、defint_autostepで、定積分
\int_a^b f(x) dx
を計算するとき、終端値bが区間(例えば\pi)だと無限ループ(あるいは非常に長時間のループ)に陥ってしまうことがあるというバグです。この関数は、(尺取り虫のように自動的に計算精度を見ながら)積分区間を
a=t_0, t_1, t_2, \ldots, t_{n-1}, t_n=b
のように分割して積分を行っていますが、そのプロセスは2passになっていて、t_iでTaylor展開の係数を計算して適切なstep sizeを推定し、[t_i,t_{i+1}]での精度保証付きの積分値を計算し、その区間幅を見て広すぎるか狭すぎるかしたら再度step sizeを修正してもう一度精度保証付きの積分値を計算する、ということをしています。ここで、[t_i,t_{i+1}]での積分値を計算するとき、t_iかt_{i+1}のどちらかが(幅が広めの)区間だった場合は積分値の計算結果の区間幅が極端に大きくなり、精度を出そうとしてt_{i+1}を引き戻してstep sizeを小さくしようとします(そんなことをしても精度は上がらないのですが)。従って、bが区間だった場合には[t_i,t_{i+1}=b]と最後の一歩を計算しようとすると、精度不足でt_{i+1}が引き戻されてしまい、いつまで経ってもbに到達しない、という現象が発生していました。最後の一歩のときはstep sizeの見直しをしないように修正しました。ずっと存在していたバグですが、0.4.51以前は最後の一歩の区間幅の再計算が広めになるバグがあってたまたま発生しづらくなっていて、0.4.52で直ったことにより顕在化したようです。この現象は、浅井 大晴さん、多田 秀介さん、宮内 洋明さんの3名の、Bessel関数J_0(x)の計算が終わらないという指摘で気付きました。Bessel関数は、\displaystyle J_n(x) = \frac{1}{\pi} \int_0^{\pi} \cos(x \sin t - nt) dt で計算しており、終端値が区間である積分をしていたので、この現象が発生しました。みなさま、ありがとうございました。
2021/08/05(木)調和級数の部分和で遊んでみた
はじめに
次のようなツイートが話題になったことがありました。調和級数
H_n = \sum_{k=1}^n \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}
が、n \to \inftyのとき無限に発散することはよく知られています。この発散は非常に遅く、30を超える最小のnはかなり大きな数になります。これを計算で求めようと思うと、計算時間の問題もありますが、何よりも丸め誤差の蓄積の影響が馬鹿にならず、正しいnを求めるのは案外大変です。以下、xに対してH_{n-1}<xだがH_n \ge xとなるようなnをF(x)と書くことにします。つまり、F(30)を計算したい。
精度保証せずに普通に計算
次の簡単なプログラムで、自然数なxに対してF(x)を計算できます。
#include <iostream>
#include <cmath>
int main()
{
double s, tmp;
long long int i;
std::cout.precision(17);
s = 0;
i = 1;
while (true) {
tmp = s + 1.0 / i;
if (floor(tmp) != floor(s)) {
std::cout << i-1 << ":" << s << "\n";
std::cout << i << ":" << tmp << "\n";
}
s = tmp;
i++;
}
}
計算結果は、| x | F(x) |
|---|---|
| 2 | 4 |
| 3 | 11 |
| 4 | 31 |
| 5 | 83 |
| 6 | 227 |
| 7 | 616 |
| 8 | 1674 |
| 9 | 4550 |
| 10 | 12367 |
| 11 | 33617 |
| 12 | 91380 |
| 13 | 248397 |
| 14 | 675214 |
| 15 | 1835421 |
| 16 | 4989191 |
| 17 | 13562027 |
| 18 | 36865412 |
| 19 | 100210581 |
| 20 | 272400600 |
| 21 | 740461601 |
| 22 | 2012783315 |
| 23 | 5471312310 |
| 24 | 14872568832 |
| 25 | 40427833562 |
| 26 | 109894245237 |
| 27 | 298723533129 |
| 28 | 812014582525 |
| 29 | 2207275035877 |
| 30 | 6000125006292 |
区間演算してみる
kvライブラリを使って、区間演算でこれが正しいかチェックしてみます。部分和を区間演算して、xを「またいで」いないかどうかチェックします。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
typedef kv::interval<double> itv;
// typedef kv::interval< kv::dd > itv;
int main()
{
itv s, tmp;
long long int i;
std::cout.precision(17);
s = 0;
i = 1;
while (true) {
tmp = s + 1.0 / itv(i);
if (floor(tmp.lower()) != floor(tmp.upper())) {
std::cout << "warning\n";
std::cout << i-1 << ":" << s << "\n";
std::cout << i << ":" << tmp << "\n";
break;
} else if (floor(tmp.lower()) != floor(s.lower())) {
std::cout << i-1 << ":" << s << "\n";
std::cout << i << ":" << tmp << "\n";
}
s = tmp;
i++;
}
}
これを実行すると、x=16のときは
\begin{eqnarray*}
&& H_{4989190} \in [15.999999890595899,15.999999899456953] \\
&& H_{4989191} \in [16.000000091029196,16.000000099890251]
\end{eqnarray*}
となって間違いなくF(16)=4989191と証明されました。しかし、x=17のときは、
\begin{eqnarray*}
&& H_{13562026} \in [16.999999921467317,16.999999960785197] \\
&& H_{13562027} \in [16.999999995202607,17.00000003452049]
\end{eqnarray*}
となってしまい、F(17)=13562027とは断定できないことが分かりました。なお、このプログラムは単に和を左から足していますが、すべて正のたくさんの数を足すときは、小さい順に足した方が丸め誤差が小さくなり、区間演算の場合は区間の幅が小さくなることが知られています。大体のnが分かっているならば、逆順に足すことによってもう少し頑張れて、F(17)=13562027、F(18)=36865412まで証明することができます。
double-double区間演算で頑張る
倍精度ではF(16)まで、逆順に足す工夫をしてもF(18)までしか証明できませんでした。kvライブラリはdouble型を2つ束ねた疑似4倍精度で区間演算ができるので、それを使って頑張ってみました。上に挙げたプログラムの最初の方のtypedef行を変更するだけです。これで計算すると、x=30で
\begin{eqnarray*}
&& H_{6000022499692} \in [29.999999999999855,29.999999999999856] \\
&& H_{6000022499693} \in [30.000000000000021,30.000000000000022]
\end{eqnarray*}
となり、F(30)=6000022499693と判明しました。最初のtweetを見て計算してみた人は何人かいたようですが、やはり丸め誤差まみれになってしまってぴったりの値を計算するのは難しかったようです。ただ、この計算にはOpenMPを使って並列化しても55時間ほどかかりました(汗)。計算結果をまとめておきます。
| x | F(x) |
|---|---|
| 2 | 4 |
| 3 | 11 |
| 4 | 31 |
| 5 | 83 |
| 6 | 227 |
| 7 | 616 |
| 8 | 1674 |
| 9 | 4550 |
| 10 | 12367 |
| 11 | 33617 |
| 12 | 91380 |
| 13 | 248397 |
| 14 | 675214 |
| 15 | 1835421 |
| 16 | 4989191 |
| 17 | 13562027 |
| 18 | 36865412 |
| 19 | 100210581 |
| 20 | 272400600 |
| 21 | 740461601 |
| 22 | 2012783315 |
| 23 | 5471312310 |
| 24 | 14872568831 |
| 25 | 40427833596 |
| 26 | 109894245429 |
| 27 | 298723530401 |
| 28 | 812014744422 |
| 29 | 2207284924203 |
| 30 | 6000022499693 |
| x | F(x) |
|---|---|
| 23 | 5471312310 |
| 24 | 14872568832 |
| 25 | 40427833562 |
| 26 | 109894245237 |
| 27 | 298723533129 |
| 28 | 812014582525 |
| 29 | 2207275035877 |
| 30 | 6000125006292 |
もうちょっと数学っぽく
有名なOEISを調べてみると、この数列はA002387に見つかりました。そこにはF(28)=812014744422まで載っていました。また、そのページからリンクされたここにはF(2303)まで(!)載っていますが、これが証明されたものかどうかは分かりません。自然数n>1に対して
F(n) = \lfloor \exp(n - \gamma) + \frac{1}{2} \rfloor
(\lfloor\rfloorはガウス記号、\gammaはEuler's gamma)という予想があるようなので、これで計算したものなのかも。また、ガンマ関数の対数微分であるディガンマ関数
\mathrm{digamma}(x) = \frac{d}{dx}\log\Gamma(x) = \frac{\Gamma'(x)}{\Gamma(x)}
は、漸化式
\mathrm{digamma}(x+1) = \mathrm{digamma}(x) + \frac{1}{x}
を満たすことが知られており、これから直ちに、
H_n = \sum_{k=1}^n \frac{1}{k} = \mathrm{digamma}(n+1) - \mathrm{digamma}(1)
が従います。よって、与えられたxに対して、
n = \lfloor \exp(x - \gamma) + \frac{1}{2} \rfloor
で予測して、H_{n-1}とH_nを精度保証付きのディガンマ関数で計算し、
H_{n-1} < x \le H_n
が満たされていればF(x)=nが証明されたことになります。幸いなことにkvライブラリには精度保証付きのディガンマ関数があるので、これを実装してみたところ、まったく精度が出ず話になりませんでした。原因はちょっと考えたらすぐ分かって、そもそもkvのディガンマ関数は
\mathrm{digamma}(x+1) = \mathrm{digamma}(x) + \frac{1}{x}
の漸化式を用いて1 \le x < 2の範囲に引き戻して計算する実装になっていて、何のことはない、ただ調和級数の部分和を計算するだけになっていたのでした。そこで、kv-0.4.52ではもうちょっと真面目にディガンマ関数を実装してみたという話でした。詳細はガンマ関数の精度保証付き計算メモの3章に書きましたが、簡単に言えば、xを引き戻した上で
\mathrm{digamma}(x) = \int_0^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-xt}}{1-e^{-t}} \right) dt
を精度保証付き数値積分で計算していたのを、引き戻しを行わずに、
\mathrm{digamma}(x) = \log x - \frac{1}{2x} - 2 \int_0^\infty \frac{t}{(t^2+x^2)(e^{2 \pi t}-1)}dt
を使って計算するようにしました。
#include <iostream>
#include <kv/interval.hpp>
#ifdef DD
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
#endif
#include <kv/gamma.hpp>
#ifdef DD
typedef kv::interval<kv::dd> itv;
#define MAX 66
#else
typedef kv::interval<double> itv;
#define MAX 32
#endif
int main() {
#ifdef DD
std::cout.precision(34);
#else
std::cout.precision(17);
#endif
itv gamma, x, y;
int i;
gamma = - kv::digamma(itv(1.));
for (i=2; i<=MAX; i++) {
std::cout << i << "\n";
x = i;
y = floor(mid(exp(x - gamma) + 0.5));
std::cout << y.lower() << "\n";
std::cout << kv::digamma(y) + gamma << "\n";;
std::cout << kv::digamma(y + 1) + gamma << "\n";;
}
}
新しいディガンマ関数を用いて計算すると、倍精度で
\begin{eqnarray*}
&& H_{16309752131261} \in [30.99999999999995,30.999999999999997] \\
&& H_{16309752131262} \in [31.000000000000014,31.000000000000061]
\end{eqnarray*}
となってF(31)=16309752131262が、double-doubleを使うと、
\begin{eqnarray*}
&& H_{9516116398696941841501814186} \in [64.99999999999999999999999999997317,64.99999999999999999999999999999567] \\
&& H_{9516116398696941841501814187} \in [65.00000000000000000000000000007849,65.00000000000000000000000000010098]
\end{eqnarray*}
となってF(65)=9516116398696941841501814187まで証明できました。数学としては何の意味もない問題でしょうけど、こういうのは楽しいですね。
2021/08/05(木)kv-0.4.52
変更点は以下の通りです。
- test-rounding.ccで、非正規化数を強制的に0にする"flush to zero"モードになっていないかどうかをチェックするようにした。
- iccでコンパイルできるように修正。
- optimize.hppで、「端にない」区間で傾きが単調ならばそこに最小値は存在しない というチェックを入れる改良を行った。
- defint-newtoncotes.hpp, double-newtoncotes.hppで、最適な分割数の 推定がうまくできていなかったバグを修正。
- defint.hpp, defint-singular.hppで、急減少関数などの特定の被積分関数 に対してstep sizeがうまく計算できていなかった問題を修正。
- psa.hppの中のinv関数を、係数のオーバーフローが発生しづらいように改良。
- gamma.hppの中のdigamma関数の計算アルゴリズムをより高精度なものに変更。
- その他細かい修正。
また、digammaを高精度化したのは、ある問題を解くのに必要になったためです。忘れないうちにその話も記事にするつもりです。