2017/08/23(水)kv-0.4.42
今回は大きな変更はありません。
- コンパイル時にマクロKV_USE_TPFMAを定義すると、twoproductの計算にfma命令を使うようになる。
- dka.hpp (Durand Kerner Aberth法) の重解時の安定性が向上。
- 精度保証付き数値計算とkvライブラリの概要を説明するスライドを掲載
2017/08/08(火)二重振り子の精度保証付き数値計算
わずかに異なる初期値をもった50本の二重振り子のシミュレーションを動画にしたもので、途中まで完全に重なっているように見える振り子が一気にバラける様子がとても面白い。
次は、それを三重振り子にしたもの。
gmpを用いて高精度計算をしており、ねとらぼで記事にもなりました。
どちらも常微分方程式の計算にはルンゲクッタ法を用いています。わずかな初期値のずれが後に大きな違いをもたらすことがとてもよく分かる動画ですが、一方で、ルンゲクッタ法で計算された値も真値とはわずかにずれており、当然その誤差も同様に後で大きな違いをもたらすことになります。だとすると、果たして意味のある計算になっているのかという疑問が生じます。
そこで、二重振り子の軌道を精度保証付きで計算し、ルンゲクッタ法とどのくらいずれるのか検証してみました。そのtweetがこれです。
このように、4次のルンゲクッタ法(刻み幅2^{-7})と精度保証付き計算とを比較してみると、t=8あたりから先は完全に違う軌道になってしまっていることが分かりました。
以下では、twitterに書けなかった細かい情報を備忘録も兼ねて書いておこうと思います。
使った式は、
\begin{align*}
& (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)
+ m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)
+(m_1+m_2)g \sin \theta_1= 0 \\
& l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2}
-l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0
\end{align*}
のようなものです(Wikipediaの記事と全く同じです)。舞台設定は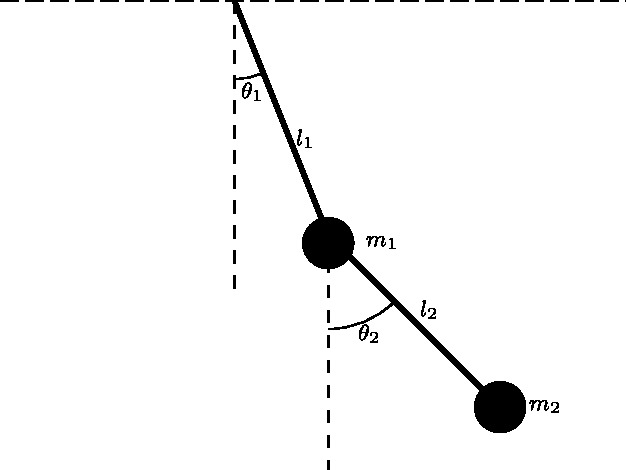
の通り。この式を\ddot{\theta_1}, \ddot{\theta_2}の2変数連立一次方程式と見て解いて正規形に直し、\dot{\theta_1}=\phi_1, \dot{\theta_2}=\phi_2のように置き直して1階4変数の常微分方程式とします。パラメータは
\begin{align*}
m_1 &= m_2 = 1 \\
l_1 &= l_2 = 1 \\
g &= 9.8 \\
\end{align*}
とし、初期値は
\begin{align*}
\theta_1(0) &= \frac{3}{4}\pi \\
\theta_2(0) &= \frac{3}{4}\pi \\
\dot{\theta_1}(0) &= 0 \\
\dot{\theta_2}(0) &= 0
\end{align*}
としました。kvライブラリを用いて、この初期値問題を精度保証付きで計算するプログラムと、4次のルンゲクッタ法で計算するプログラムを書きました。両方のプログラムをzipで上げておきます ( doublependulum.zip )。4次のルンゲクッタ法の刻み幅は固定で2^{-7}としました。精度保証付きの方は全ての時刻の解を多項式の形で連続的に計算しているのですが、ルンゲクッタ法と同じ2^{-7}の刻み幅で密出力させています。この計算結果を動画にしたものが、先のtweetというわけです。
プログラムを走らせて得られた生データを上げておきます ( doublependulum-result.zip )。t=1のときの両プログラムのデータを抜き出すと、
| \theta_1 | \theta_2 | |
|---|---|---|
| kv | [ 0.14046540255551162,0.14046540255558421] | [ -0.71766989300731332,-0.71766989300724726] |
| rk4 | 0.1404652582264235 | -0.71766977132932186 |
このデータをグラフにしてみました。
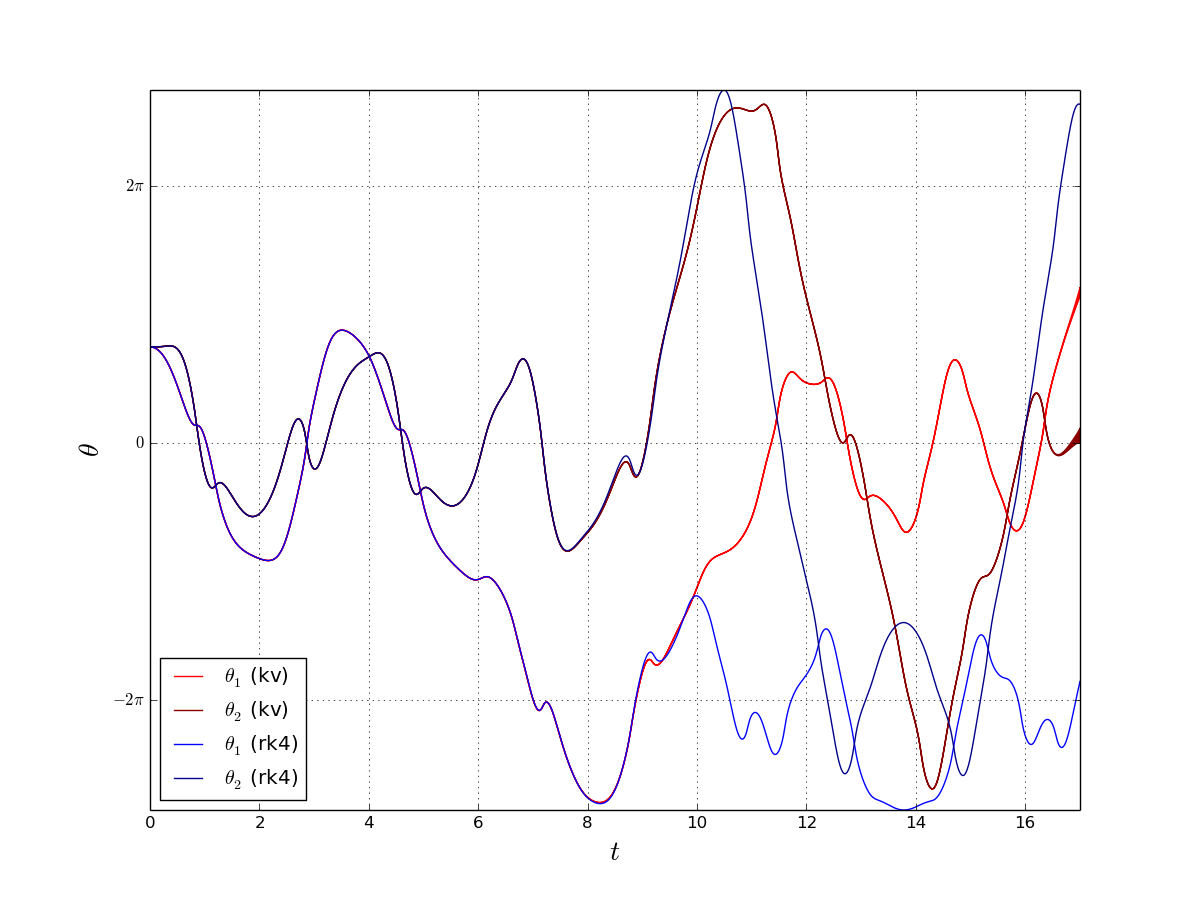
t=8付近でずれが目に見えるようになり、そのあとは完全に異なる軌道を描いています。
精度保証付き計算もいつまでも高精度を保っていられるわけではなく、t=17付近を見るとわずかにグラフに幅があるのが分かります。この後一気に区間幅が爆発し、t=17.05付近で計算不能に陥ります。この精度保証付き計算プログラムはgmpのような高精度数を使用しているわけではなく、内部で使っているのは普通のdoubleです。試しに内部の数値型をdd(擬似4倍精度数)に変えてみたところ、t=30くらいまでは普通に破綻すること無く計算出来ました。
二重振り子の動画を見るだけなら、精度保証してもしなくても動きの「印象」はほとんど変わらないのですが、カオス系に対して数値シミュレーションで何らかの数学的な結論を得ようと思うならば、誤差が明確に把握できる精度保証付き数値計算は必須だと思います。みなさま、精度保証付き数値計算を使いましょう!
2017/03/21(火)Henon mapで遊んでみた
Hénon mapは、
\begin{pmatrix}
x_{n+1} \\
y_{n+1}
\end{pmatrix}
=
\begin{pmatrix}
1 + y_n - a x_n^2 \\
b x_n
\end{pmatrix}
みたいな漸化式で定義される2次元離散力学系です。a,bの値によってはカオスになることで有名な力学系で、a=1.4、b=0.3がカオスになる有名な値です。その値を使って(x,y)=(0,0)から10000点計算してxy平面にプロットしてみると、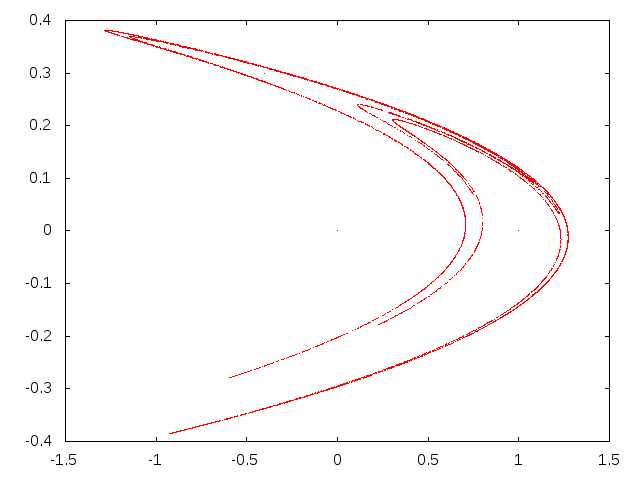
のような図形が得られました。
さて、適当な点から出発してn回反復したとき元の点に戻るような軌道をn周期解と言います。周期解には、一度その軌道に入ったらずっとそこから出ない安定な周期解と、わずかな摂動で軌道から外れてしまう不安定な周期解があります。一般にカオスになるときは不安定な周期解しか無いのが普通ですが、よく使われるa=1.4, b=0.3でなく、そこからわずかに値を変化させると安定な周期解が現れることが知られていて、そのような安定な周期解をどうやって探索するか、が講演の内容でした(多分)。
で、とりあえずkvライブラリを使って周期解の探索をしてみよう、というのが以下の内容です。とりあえずa=1.4, b=0.3で、(x,y)の探索範囲は、この論文にあった式
r = \frac{1+|b|+\sqrt{(1+|b|)^2+4a}}{2}
を使って(x,y)\in([-r,r],[-r,r])で探索することにしました。n回反復する写像の不動点を全解探索するプログラムを素直に書くと、
#include <kv/allsol.hpp>
namespace ub = boost::numeric::ublas;
template <class TT>
struct Henon {
TT a, b;
Henon(TT a, TT b) : a(a), b(b) {}
template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
ub::vector<T> r(2);
r(0) = 1 + x(1) - a * x(0) * x(0);
r(1) = b * x(0);
return r;
}
};
template <class F>
struct Repeat_n {
F f;
int n;
Repeat_n(F f, int n): f(f), n(n) {}
template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
int i;
ub::vector<T> tmp;
tmp = x;
for (i=0; i<n; i++) tmp = f(tmp);
return tmp;
}
};
template <class F>
struct FixedPoint {
F f;
FixedPoint(F f): f(f) {}
template <class T> T operator() (const T& x){
return f(x) - x;
}
};
typedef kv::interval<double> itv;
int main()
{
int i, n;
ub::vector<itv> x;
itv a, b;
itv::base_type r;
std::cout.precision(17);
a = "1.4";
b = "0.3";
n = 4;
Henon<itv> f(a, b);
Repeat_n< Henon<itv> > g(f, n);
FixedPoint< Repeat_n< Henon<itv> > > h(g);
r = ((1+abs(b)+sqrt(pow(1+abs(b), 2)+4*a))/2).upper();
x.resize(2);
x(0) = itv(-r, r);
x(1) = itv(-r, r);
kv::allsol(h, x);
}
のようになりました(henon0.zip)。関数オブジェクトを使っていて、fがHénon写像、gがそれをn回繰り返したもの、hが不動点形式(g(x)-x)です。このプログラムをnを変えながら実行してみます。n=1では、([-1.1313544770895053,-1.131354477089504],[-0.33940634312685164,-0.33940634312685119])の2つの1周期解(要するに不動点)が得られました。n=2にすると、
([0.63135447708950442,0.63135447708950499],[0.18940634312685131,0.18940634312685154])
([-0.47580005117505659,-0.47580005117505597],[0.29274001535251664,0.29274001535251721])の4つの解が得られましたが、よく見るとそのうち2つは先程得られた不動点です。更に、残りの2つの解も実質同じ軌道(p→q→pが2周期解ならq→p→qも当然2周期解)なので、2周期解は実質1つだけということが分かります。n=3だと、
([0.97580005117505597,0.97580005117505653],[-0.14274001535251713,-0.14274001535251665])
([0.63135447708950431,0.6313544770895051],[0.18940634312685117,0.18940634312685171])
([-1.1313544770895053,-1.131354477089504],[-0.33940634312685198,-0.33940634312685086])
([-1.1313544770895053,-1.131354477089504],[-0.33940634312685298,-0.33940634312684986])が得られますが、これは不動点なので、3周期解は存在しないことが分かりました。n=4の結果を示すと、
([0.6313544770895042,0.63135447708950521],[0.18940634312685095,0.18940634312685187])
([0.63135447708950431,0.6313544770895051],[0.18940634312685045,0.1894063431268524])と8つの解が得られますが、2つは不動点、2つは2周期解で、4周期解は位相をずらした4つが得られるので実質1つの4周期解があることが分かります。
([0.63819399262715537,0.63819399262715638],[-0.21203003316582356,-0.2120300331658213])
([-0.70676677721940862,-0.70676677721940761],[0.33752098096070709,0.33752098096070832])
([0.2177617657186289,0.21776176571863363],[0.19145819778814535,0.19145819778814813])
([-0.47580005117505797,-0.47580005117505475],[0.2927400153525157,0.29274001535251815])
([-1.1313544770895064,-1.1313544770895032],[-0.33940634312685631,-0.33940634312684653])
([0.97580005117505508,0.97580005117505731],[-0.14274001535251838,-0.1427400153525154])
([1.1250699365356913,1.1250699365356934],[0.065328529715587863,0.065328529715590903])
さて、このように人間の目で選り分けるのは大変なので、より短い周期解の繰り返しや位相がずれただけのものを排除する部分を付け加えて見ました。ついでに、その周期解の安定性をその写像の解のところでのヤコビ行列を計算しその固有値の絶対値の最大値を調べることによって判定する部分も付けてみました。
#include <kv/allsol.hpp>
#include <kv/eig.hpp>
namespace ub = boost::numeric::ublas;
template <class TT>
struct Henon {
TT a, b;
Henon(TT a, TT b) : a(a), b(b) {}
template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
ub::vector<T> r(2);
r(0) = 1 + x(1) - a * x(0) * x(0);
r(1) = b * x(0);
return r;
}
};
template <class F>
struct Repeat_n {
F f;
int n;
Repeat_n(F f, int n): f(f), n(n) {}
template <class T> ub::vector<T> operator() (const ub::vector<T>& x){
int i;
ub::vector<T> tmp;
tmp = x;
for (i=0; i<n; i++) tmp = f(tmp);
return tmp;
}
};
template <class F>
struct FixedPoint {
F f;
FixedPoint(F f): f(f) {}
template <class T> T operator() (const T& x){
return f(x) - x;
}
};
typedef kv::interval<double> itv;
int main()
{
int i, n;
std::list< ub::vector<itv> > result, result2;
std::list< ub::vector<itv> >::iterator p, p2;
ub::vector<itv> x, x2;
bool flag;
itv a, b;
itv::base_type r;
std::cout.precision(17);
a = "1.4";
b = "0.3";
n = 4;
Henon<itv> f(a, b);
Repeat_n< Henon<itv> > g(f, n);
FixedPoint< Repeat_n< Henon<itv> > > h(g);
r = ((1+abs(b)+sqrt(pow(1+abs(b), 2)+4*a))/2).upper();
x.resize(2);
x(0) = itv(-r, r);
x(1) = itv(-r, r);
result = kv::allsol(h, x);
p = result.begin();
while (p != result.end()) {
x = *p;
flag = true;
x2 = x;
for (i=0; i<n-1; i++) {
x2 = f(x2);
// check the solution is truly n-pediodic or not
if (overlap(x, x2)) {
flag = false;
break;
}
// check the solution is new or not
p2 = result2.begin();
while (p2 != result2.end()) {
if (overlap(*p2, x2)) {
flag = false;
break;
}
p2++;
}
if (flag == false){
break;
}
}
if (flag) {
result2.push_back(x);
std::cout << "true pediodic soluion " << result2.size() << "\n";
x2 = x;
for (i=0; i<n; i++) {
std::cout << x2 << "\n";
x2 = f(x2);
}
std::cout << "\n";
// calculate maximum eigenvalue of Jacobian
ub::vector<itv> v1;
ub::vector< kv::complex<itv> > l;
itv lm, tmp;
ub::matrix<itv> m1;
kv::autodif<itv>::split(g(kv::autodif<itv>::init(x)), v1, m1);
kv::veig(m1, l);
std::cout << l << "\n";
lm = 0;
for (i=0; i<2; i++) {
tmp = abs(l(i));
lm.lower() = std::max(lm.lower(), tmp.lower());
lm.upper() = std::max(lm.upper(), tmp.upper());
}
std::cout << lm << "\n";
if (lm < 1) {
std::cout << "stable\n";
} else if (lm > 1) {
std::cout << "unstable\n";
} else {
std::cout << "stability unknown\n";
}
}
p++;
}
}
(henon1.zip) これで調べた周期解とその安定性は次のとおりです。| n | x | y | 安定性 |
|---|---|---|---|
| 1 | [-1.1313544770895053,-1.131354477089504] | [-0.33940634312685164,-0.33940634312685119] | unstable |
| 1 | [0.63135447708950442,0.63135447708950499] | [0.18940634312685131,0.18940634312685154] | unstable |
| 2 | [-0.47580005117505659,-0.47580005117505597] | [0.29274001535251664,0.29274001535251721] | unstable |
| 4 | [0.63819399262715537,0.63819399262715638] | [-0.21203003316582356,-0.2120300331658213] | unstable |
| 6 | [0.44190995135922078,0.44190995135922451] | [-0.24126597029523553,-0.24126597029522911] | unstable |
| 6 | [1.0380595354868291,1.0380595354868339] | [0.093435694641492983,0.093435694641505183] | unstable |
| 7 | [-1.0872860458490461,-1.0872860458490447] | [0.36967525887581315,0.36967525887581654] | unstable |
| 7 | [-1.0466775735267937,-1.0466775735267894] | [0.35496793781757529,0.35496793781758157] | unstable |
| 7 | [-0.92617327728451871,-0.92617327728451703] | [0.34236913808086111,0.3423691380808675] | unstable |
| 7 | [0.81803519601224594,0.81803519601224873] | [0.15474440787832016,0.15474440787832872] | unstable |
| 8 | [-1.1493133062560075,-1.1493133062560048] | [0.36560087176430355,0.36560087176431478] | unstable |
| 8 | [-0.8274542278695698,-0.82745422786956712] | [-0.37646388947765531,-0.37646388947764258] | unstable |
| 8 | [0.90002978920450349,0.90002978920451305] | [0.13188647717963458,0.13188647717967495] | unstable |
| 8 | [-0.44837319092732131,-0.44837319092731264] | [-0.34223569372342872,-0.34223569372341905] | unstable |
| 8 | [-0.83680827077054099,-0.83680827077053698] | [0.35013340845532586,0.35013340845533498] | unstable |
| 8 | [-0.80876720316291007,-0.80876720316289762] | [0.32983594103956154,0.32983594103958375] | unstable |
| 8 | [0.60111180966072053,0.6011118096607403] | [-0.21508292460527792,-0.21508292460523506] | unstable |
| n | 周期解の数 |
|---|---|
| 1 | 2 |
| 2 | 1 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 2 |
| 7 | 4 |
| 8 | 7 |
| 9 | 6 |
| 10 | 10 |
| 11 | 14 |
| 12 | 19 |
| 13 | 32 |
さて、この論文によると、a=1.3866414978735625,b=0.3だと、8周期の安定解が存在するのだそうです。実際、aの値をそれに変えて計算してみると、
| n | x | y | 安定性 |
|---|---|---|---|
| 8 | [0.8742591352635014,0.87425913526350741] | [0.14575249177868274,0.14575249177870631] | unstable |
| 8 | [-0.84160148826306525,-0.84160148826306058] | [0.35209093466818297,0.35209093466819364] | unstable |
| 8 | [-0.4853729323948971,-0.48537293239488293] | [-0.34686239645463785,-0.34686239645462463] | unstable |
| 8 | [0.60580464136231371,0.6058046413623337] | [-0.21568623282216013,-0.21568623282211638] | unstable |
| 8 | [1.1065521562926103,1.1065521562926253] | [-0.11533020216315528,-0.11533020216311613] | unstable |
| 8 | [0.42199129139879743,0.42199129139889974] | [0.1755174868908467,0.17551748689086294] | stable |
| 8 | [0.93092246076173934,0.93092246076183872] | [0.12609408826805895,0.12609408826806834] | unstable |
\begin{pmatrix}
[-0.2071075038203655,-0.20710750356848622] & [1.3046842272497074,1.3046842274628959]) \\
[0.046141607262891293,0.046141607302409162] & [-0.29098818813819278,-0.29098818810610671]
\end{pmatrix}
で、その固有値の絶対値の最大値は[0.49796393435494867,0.49796393621891983]でした。1より小さいのでこの解は安定なことが分かります。さて、もう少し遊んでみたりもしたのですが記事も長くなってきたのでこのへんまでにしましょう。力学系方面の知識が無いのでこういう軌道を計算することがどう面白いのかはあまり分からないのですが、いろいろ楽しめました。力学系方面で精度保証付き数値計算をしたいという需要はありそうな気がするので、共同研究なんかに繋がるといいなあ。
2017/03/10(金)kv-0.4.41
今回の変更は、キャストし忘れでode solverの内部使用型をddとしたときにコンパイル出来なくなっていた修正だけです。
また、ドキュメントにkvライブラリの応用例のページを追加しました。まだ2つだけしか載せていませんが、手元には載せたい応用例がたくさんあるので今後増やしていきたいと思います。また、このページでは数式を表示するプラグインのMathJaxを使ってみました。何か不具合があればお知らせください。
2017/01/27(金)kv-0.4.40
今回は、T大のT先生の依頼によるODE solver仕様変更が含まれています。その他、psaのドキュメントを最新にしたり、kraw_approxの1変数版を追加したりしました。
ODE solverの仕様変更は以下のようなものです。常微分方程式の計算を行なうodelong_maffineなどのodelong系の関数では、計算しながら何かをさせるためのcallback関数を指定する機能があります (正確に言うと、()演算子を持つcallback用のオブジェクト)。これの戻り値は今まではvoidだったのですが、それをboolに変更してその値をチェックするようにし、もしfalseなら計算を中止するようにしました。これにより、終了条件として時刻でなく、「値が何かの条件を満たしたら終了」のようなことが出来るようになりました。これは便利になっているのですが、もし今までのversionのkvを利用していてcallback関数を継承によりカスタマイズする機能を使っていた場合、コンパイルエラーになってしまうという申し訳ないことになってしまいました。修正は簡単で、operator()を定義する関数の戻り値をboolに変えて末尾にreturn true;を補うだけです。
こういうことはなるべく起きないように仕様を考えるときは気をつけていたのですが、今回はメリットが仕様変更のデメリットを上回ると考えてこうすることに決心しました。恐らくこの機能を実際に使っているのはT大のT先生だけだと思いますが、もし他に使っている方がいらっしゃれば大変申し訳ありません。
また、githubの方のソースコードも最新になっています。結局ローカルの開発体制をgitに移行するには至らず、version up時にまとめてgithubを更新するような何とも無意味な状態になっています。新しいものに馴染むのは難しい…