kashiの日記

検索条件

タグで絞り込みその他(2)

日付で絞り込み 2013年(7) 2014年(31) 2015年(22) 2016年(17) 2017年(6) 2018年(7) 2019年(2) 2020年(1) 2021年(6) 2022年(3) 2024年(2)

全104件 (7/21ページ) 一覧表示に切り替え記事本文を表示

2016/12/03(土)double-double演算が異常に高精度になる!?

いわゆるdouble-doubleによる4倍精度演算が不思議な挙動を示した例を見つけたので、メモしておきます。

いわゆる普通の電卓で、適当な数(例えば100)を入れて、平方根のボタンを何回か押して、次に二乗(多くの電卓で[×][=]という操作)を同じ回数だけ行います。このとき、その回数がある程度以上多いと、丸め誤差でちゃんと100に戻ってきません。100円ショップに売っていた8桁のごく普通の電卓で試してみたところ、

100 → (10回平方根) → 1.0045072 → (10回二乗) → 99.9806

と、誤差が観測されました。更に回数を増やしてみると、

100 → (20回平方根) → 1.0000042 → (20回二乗) → 81.635475

100 → (25回平方根) → 1 → (25回二乗) → 1

のようになりました。平方根を取った値は徐々に1に近づき、1+εのεを保持する桁数が徐々に小さくなっていって、誤差がひどくなっていく様子がよく分かります。

もちろん、普通のPCで倍精度(double)を用いても同じことで、誤差が入ります。

#include <iostream>
#include <cmath>

int main()
{
	int i;
	double x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}

を実行すると、

100.00000000000637

のように誤差が入りました。kvライブラリを使って区間演算にしてみます。

#include <kv/interval.hpp>
#include <kv/rdouble.hpp>

typedef kv::interval<double> itv;

int main()
{
	int i;
	itv x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}

すると、

[99.99999999997776,100.00000000004346]

のように100を含む区間が得られます。

さて、ここからが本題です。このdoubleで区間演算をしたときの区間幅を、平方根と二乗の回数を変化させながらプロットしてみます。

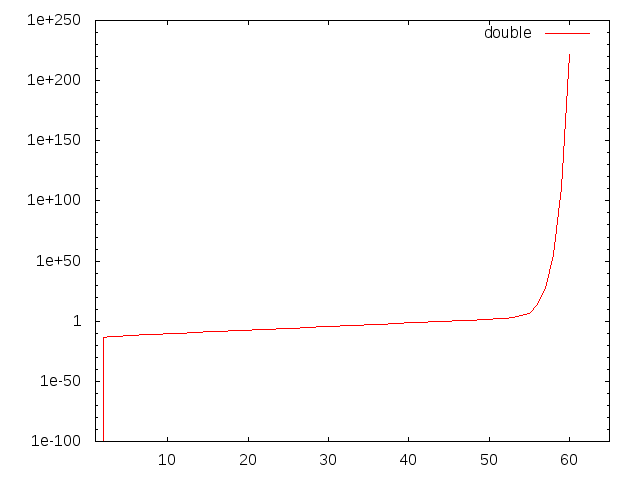
60回手前で計算が破綻していることが分かります。どこまで行けるかは仮数部の長さで決まる筈なので、mpfrを使って仮数部長を変化させて比較してみます。

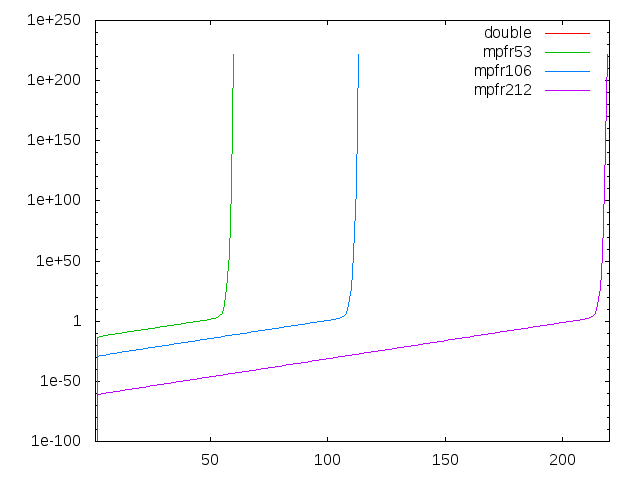
すると、mpfrの仮数部を53bit(doubleと同じ)にした場合はdoubleとぴったり同じ、mpfrの仮数部長を長くすればそれだけ破綻までの回数が大きくなっています。ここまでは予想通り。ここで、このグラフにdd(double-double演算による擬似4倍精度、仮数部は106bit相当)を追加してみましょう。

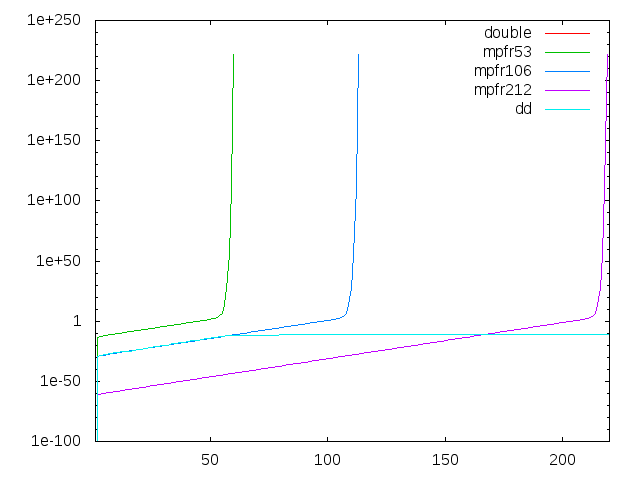
なんだか異常なグラフが得られました。仮数部106bit相当なのでmpfr106と同じ動きをすると思いきや、最初は同じ挙動を示すものの途中から全く精度の悪化が見られず、mpfr212をも凌ぐ精度を叩きだしています。そんな馬鹿なとmpfrの超高精度を追加してみます。

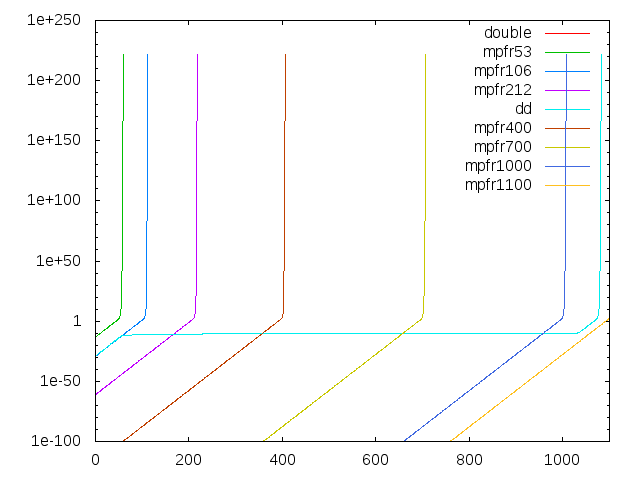
すると、mpfrの仮数部1100bitで、ようやくddに勝つことができました。この現象は、

#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>

typedef kv::interval< kv::dd > itv;

int main()
{
	int i;
	itv x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}

のようなプログラムで区間幅を観察すれば容易に確かめられます。

さて、なぜこんなことが起きたのでしょうか。最初はバグを疑ったのですが、バグではありませんでした。後日この現象の原因を追記しようと思いますので、少し考えてみて下さい。

解答 (12月4日追記)

一日経ったので理由を簡単に説明します。

まず、ddとmpfr106で、平方根を40回行った場合の値を見比べてみます。表示は40桁にしました。

[1.000000000004188377884927590880100368969,1.000000000004188377884927590880168161704] (dd)
[1.000000000004188377884927590880118857896,1.000000000004188377884927590880168161704] (mpfr106)

ここではほぼ違いは見られません。上限と下限で一致している桁数は32桁で、4倍精度としては普通です。次に、平方根を80回にしてみます。

[1.000000000000000000000003809307495356531,1.000000000000000000000003809307495356571] (dd)
[1.000000000000000000000003809307449647879,1.000000000000000000000003809307498951686] (mpfr106)

こちらは顕著な違いが見られます。mpfrの方は32桁で変わっていませんが、ddの方は38桁も一致していることが分かります。

これは、ddの内部表現の特殊性によるものです。ddは、簡単にいうと仮数部の上位53bitと下位53bitを分割して格納するようなフォーマットです。よって、上位と下位の指数部は53ずれるのが普通なのですが(正確には下位の符号が利用できるので54ずれる)、上位と下位の間に0(上位と下位の符号が違う場合は1)が連続するような場合、それを省略することができ、上位と下位の指数部のずれが大きくなって仮数部長が大きくなることがあります。この場合も、40回のときの値の内部表現を見ると、

1.000000000004188427382700865564-4.9497773274684e-17

ですが、80回のときは

1+3.8093074953565e-24

で上位と下位が大きく離れています。たまたま収束先が1(=doubleで正確に表現可能)で、1+εのεの精密な表現力が問われるような問題だったので、ddが異常に高精度になったという仕掛けでした。

極めてレアな現象でいつもこういうことが起きるわけではないですが、偶然出会ったので記事に残しておきたくなったのでした。

コメント（0件）

2016/11/20(日)kv-0.4.37

精度保証

kvライブラリを久しぶりに0.4.37にアップデートしました。

今回は、double-double (dd) 関連のアップデートです。ddのsqrtが(多分)精度が上がって速くなっています。また、sqrtに無限大を入れた時にNaNになってしまっていたバグを修正しました。

そして、重大なバグ修正を含んでいます。0.4.36までは、ddを内部に持つ区間演算 interval<dd> の除算において、ある特定の条件のときに丸めの向きを間違うバグがあり、精度保証されていなかった可能性があります。interval<dd> を使って何らかの精度保証を行っている方は、速やかに0.4.37にアップデートをお願いします。近似計算としてddを使っている場合は問題ありません。

また、ddに関してはそれなりに利用者がいるにもかかわらずきちんとした形でアルゴリズムを記載していませんでした。今回、

double-double演算とdouble-double区間演算に関するまとめ

を書きましたので、興味のある方は是非お読み下さい。

コメント（0件）

2016/10/02(日)scan2016

精度保証

scan2016という、精度保証付き数値計算の研究者が一同に会する研究会に参加してきました。2年に一度の開催なのですが、2年前は学科主任だったため参加できず、今回は4年ぶりの参加です。開催場所はスウェーデンのウプサラというところで、スウェーデンNo.1の大学であるウプサラ大学を中心に発展した街だそうです。

自分が発表した内容は大体5月にこの記事に書いたもので、だいぶ忘れかけていたので何というか気合いがなかなか入らなくて大変でした。行きの飛行機の中で電源が使えたのが大助かり。stiffなODEをどう効率的に精度保証するか、というのは何年も前からこの業界の大きなテーマで、それなりに印象を残せたのではないかと勝手に考えています。

この業界は狭くて研究者の数が多くないので、朝から晩までずっと精度保証の話を聞くという機会は滅多に無く、どの話も刺激的で大変満足出来ました。(こういう機会に自分の発表だけしてさっさと遊びに行っちゃう人は何を考えてるんだろう、と毒を吐いておこう。誰が何をしようと勝手だけど、そういう人とは友達になれないなあ。)

メキシコから来た某juliaおじさんのjulia押しが強力で割と印象に残りました。C++のテンプレートのような、型に合わせて何通りもの新しい関数を自動生成する機能があるようで、うまく使えば確かに精度保証付き数値計算にフィットするかなと。

また、double-doubleの誤差評価を厳密に頑張る話もなかなか楽しそう。某Y氏が数年前にやろうとしてた気がするが、それとの関係はどうなんだろうか。

Csendesの話面白かった。やはり遅延微分方程式に手を出すべきか?

Tuckerがオーガナイザーだったせいか、ODEの話が多めでしたね。国府先生の話で出てきた宮路先生のTaylorモデルの実装とか、興味あるなあ。

2年後に東京で開催することが正式に決定したので、頑張らないと!

コメント（0件）

2016/08/03(水)半精度浮動小数点数に関する思考実験

その他精度保証

半精度浮動小数点数というものがあります。よく使われている単精度(float, 32bit)、倍精度(double, 64bit)に対して、全長16bitと単精度の半分で浮動小数点数を表現するものです。IEEE754-2008でbinary16としてフォーマットが定められています。deep learningの隆盛とともに「精度が低くてもとにかく速く」計算するニーズが高まり、GPUでハードウェアサポートされるなど、最近注目を集めています(ような気がします)。

IEEE754-2008の半精度では、16bitを符号s(1bit)+指数部e(5bit)+仮数部m(10bit)に分割しています。指数部のオフセットは15で、従って正規化数は

x = (-1)^s × 1.m × 2^e-15

のように、非正規化数は

x = (-1)^s × 0.m × 2^-14

のように実数xと対応します。

ところで、URRという浮動小数点数の表現形式をご存知でしょうか。浜田穂積先生が80年代(IEEE754制定より前!)に提案された浮動小数点数の表現形式です。詳細は

を見ていただくとして、簡単に言えば、指数部と仮数部の区切りを可変にし、1に近い数(=指数部を表現するのに必要なbit数が少ない)ときには指数部を短くして仮数部を長くして精度を稼ぎ、非常に小さい数や非常に大きい数を表現するときには仮数部の長さを犠牲にして指数部に長いbitを割り当てる、というものです。このとき、何も考えずに指数部と仮数部を結合してしまうとその区切りが分からなくなってしまいますが、そこは指数部を表現するのに「bit列の末尾が分かるような自然数の表現方法」を用いることで解決します。例えば、Eliasのガンマ符号やデルタ符号といった符号化の方法がよく知られています。

さて、半精度浮動小数点数は、bit数が少ないこともあって表現できる数値の範囲が非常に狭く、簡単にアンダーフローやオーバーフローを起こしてしまいます。正の最大数は何と65504です。正の最小数は、精度を保っている正規化数で2^-14≃6.1×10^-5、非正規化数まで考えても2^-24≃5.96×10^-8にすぎません。

そこで、URR的な考え方を用いて16bit浮動小数点数を構成したらどうなるか考えてみました。URRは-infやNaNが無いなど、現代のIEEE754に慣れた我々には使いにくいところもあるので、指数部と仮数部の区切りを可変にするという思想はそのままで、適当にフォーマットを定めます。指数部は、Eliasのデルタ符号を用いることにします。デルタ符号は1,2,3,…の自然数しか表せないので、指数部とデルタ符号で表す数値を

デルタ符号	1	2	3	4	5	…	255	256	…	508	509	510	511
指数部	0	-1	1	-2	2	…	127	-128	…	-254	±0	±inf	NaN
デルタ符号の長さ	1	3	3	5	5	…	14	15	…	15	15	15	15

のように対応させることにしました。指数部の最後の3つを特殊な数に割り当てています。仮数部は、IEEE754に倣って先頭の1を格納しない「ケチ表現」にします。このフォーマットとIEEE754-2008のbinary16で、指数部と仮数部の長さの関係を表にしてみます。

	提案方式の仮数部長	IEEE754-2008の仮数部長
2^-254	1	-
⋮	⋮	⋮
2^-128	1	-
2^-127	2	-
⋮	⋮	⋮
2^-24	6	1
2^-23	6	2
2^-22	6	3
⋮	⋮	⋮
2^-16	6	9
2^-15	7	10
2^-14	7	11
⋮	⋮	⋮
2^-8	7	11
2^-7	8	11
⋮	⋮	⋮
2^-4	8	11
2^-3	11	11
2^-2	11	11
2^-1	13	11
2⁰	15	11
2¹	13	11
2²	11	11
2³	11	11
2⁴	8	11
⋮	⋮	⋮
2⁷	8	11
2⁸	7	11
⋮	⋮	⋮
2¹⁴	7	11
2¹⁵	7	11
2¹⁶	6	-
⋮	⋮	⋮
2¹²⁷	2	-
2¹²⁸	1	-
⋮	⋮	⋮
2²⁵³	1	-

これを見ると、1付近では仮数部が長くなり、1から離れると徐々に仮数部が短くなっていき、(精度は低いものの)小さな数から大きな数まで表現できていることが分かります。全長16bitなどという極端に厳しい場面でこそ、このようなフォーマットが生きると思うのですがいかがでしょうか。

もちろんハードウェアのサポートが無くソフトウェアエミュレーションでは速度は絶望的ですが、将来このような優れたフォーマットが気軽に使えるようになればいいなと思っています。FPGAとかで作って遊んだりできないかなあ。

コメント（3件）

2016/06/20(月)方向付き丸めクイズ

精度保証

唐突ですがクイズです。a, b, c, dはIEEE 754に従う浮動小数点数とします。以下の計算をIEEE754の+∞方向への丸め(上向き丸め)で行い、計算値をx, 真値をx*とします。このとき、「必ずx ≥ x*が成立する」と言えるのはどれか。○と☓で答えて下さい。但し、計算中にゼロ除算が起きるケースは除外してよいものとします。

x = a + b
x = a - b
x = a × b
x = a / b
x = (a + b) + c
x = (a × b) × c
x = (a - b) - c
x = a - (b + c)
x = -a + b
x = -( (-a) + (-b) )
x = a × b + c × d
x = (a + b) × (c + d)
x = a / (b + c)
x = a - b × c
x = a + (-b) × c
x = sqrt(a)
x = exp(a)

少し考えれば答えは分かると思いますが、これらの答えが全て○になると誤解してるのではないかという事例にたまに遭遇しますので、こういうクイズにも意味があるのではないかと思い、記事を書いてみました。

コメント（0件）