2021/12/23(木)変なベンチマークテスト
変なベンチマーク?
元々のきっかけは、のツイートでした。加減乗除が一回ずつ出てきて、発散やゼロ除算を起こさず無限に回れるループが面白いなと思いました。核心部は、
a = 123;
for (j = 0; j< 1000000000; j++) {
a = (a * a - a) / (a + a);
}
の部分です。確かに加減乗除を一回ずつ含んでいる。約分すると
a = (a - 1) /2
というループで、a=-1に収束します。ただ、初期値を-1にしたら最適化コンパイラに(ずっと-1であることを)見抜かれてしまってループを消されてしまったりしました。これに触発されて、値が一定でなく乱数のように振る舞い、最適化に消されず計算せざるを得ないような計算式はできないかなと考えてみました。
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
初期値は0.4から0.6の間の適当な値にします。すると、0.4から0.6の間を乱数のように振る舞います。元の式は分母(a*a-a)と分子(a+a)が独立に計算できるのである種の並列性を活かすことができましたが、こちらは前の計算の結果が出てこないと次の計算が始められないような構造になっています。また、元の式はa*a-aの部分をFMAを使って計算して高速化できる可能性がありますが、こちらはFMAの使える箇所がありません。つまり、最新のCPUに備わっている高速化機構を拒否するような計算になっているので、純粋な(?)計算速度を計測できると思われます。このつぶやきに続けていくつかベンチマークを流しましたが、使ったプログラムや条件等、きちんと書き残しておこうと思って書いているのが、この記事です。
いろんな言語でベンチマーク
手元のマシンに入っていたいろんな言語で、手当たり次第ベンチマークをしてみました。すべてcore i7 9700、ubuntu 20.04です。すべて普通にaptで入ったバージョンのものを使用しています。なお、計算時間計測は短いものは数回動かして目視で平均的なものを採用、長いものは一発のみ、更にVMwareの中で動かしてるのであまり厳密なものではないことをご承知おきください。C++ (gcc)
#include <iostream>
int main()
{
int i;
double x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ --version c++ (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0 Copyright (C) 2019 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. $ c++ -O3 bench.cc $ time ./a.out 0.487308 real 0m6.065s user 0m5.964s sys 0m0.000s
C++ (clang)
$ clang++ --version clang version 10.0.0-4ubuntu1 Target: x86_64-pc-linux-gnu Thread model: posix InstalledDir: /usr/bin $ clang++ -O3 bench.cc $ time ./a.out 0.487308 real 0m5.964s user 0m5.859s sys 0m0.008s
Java
class bench {
public static void main(String[] args)
{
int i;
double x;
x = 0.5;
long startTime = System.nanoTime();
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
long endTime = System.nanoTime();
System.out.println(x);
System.out.println((endTime - startTime) / 1000000000.);
}
}
$ java --version openjdk 11.0.13 2021-10-19 OpenJDK Runtime Environment (build 11.0.13+8-Ubuntu-0ubuntu1.20.04) OpenJDK 64-Bit Server VM (build 11.0.13+8-Ubuntu-0ubuntu1.20.04, mixed mode, sharing) $ javac bench.java $ java bench 0.48730753067792154 5.940579694
fortran
fortranのプログラム書いたの人生初なんだが、これでいいのかな。program bench implicit none double precision :: x integer :: i x = 0.5d0 do i=1,1000000000 x = 1 / (x * (x - 1)) + 4.6d0 end do print *, x end program bench
$ gfortran --version GNU Fortran (Ubuntu 9.3.0-17ubuntu1~20.04) 9.3.0 Copyright (C) 2019 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. $ gfortran -O3 bench.f90 $ time ./a.out 0.48730753067792154 real 0m6.154s user 0m6.045s sys 0m0.004s
nim
数日前からnimを勉強し始めました。var x = 0.5 for i in countup(1, 1000000000): x = 1 / (x * (x-1)) + 4.6 echo(x)
$ nim --version Nim Compiler Version 1.0.6 [Linux: amd64] Compiled at 2020-02-27 Copyright (c) 2006-2019 by Andreas Rumpf active boot switches: -d:release $ nim c -d:release bench.nim Hint: used config file '/etc/nim/nim.cfg' [Conf] Hint: system [Processing] Hint: widestrs [Processing] Hint: io [Processing] Hint: bench [Processing] CC: stdlib_formatfloat.nim CC: stdlib_io.nim CC: stdlib_system.nim CC: bench.nim Hint: [Link] Hint: operation successful (14486 lines compiled; 3.525 sec total; 15.961MiB pea kmem; Release Build) [SuccessX] $ time ./bench 0.4873075306779215 real 0m6.029s user 0m5.912s sys 0m0.000s
julia
インタプリタだけどJITで爆速なjulia。一回勉強しかけたけど、途中で忙しくなって忘れつつある。
function hoge(x)
for i=1:1000000000
x = 1 / (x * (x-1)) + 4.6
end
return x
end
@time print(hoge(0.5))
$ julia --version julia version 1.4.1 $ julia bench.jl 0.48730753067792154 6.103540 seconds (500.26 k allocations: 22.774 MiB)
python
大人気だけど遅いと言われるpython。実際遅い。import time def hoge(x, n): for i in range(n): x = 1 / (x * (x - 1)) + 4.6; return x; s = time.perf_counter() print(hoge(0.5, 1000000000)) e = time.perf_counter() print(e - s)
$ python --version Python 3.8.10 $ python bench.py 0.48730753067792154 75.22909699298907
python + numba
numbaを使ってJITしてみた。こういう簡単なプログラムだとちゃんと速くなる。from numba import jit import time @jit def hoge(x, n): for i in range(n): x = 1 / (x * (x - 1)) + 4.6; return x; s = time.perf_counter() print(hoge(0.5, 1000000000)) e = time.perf_counter() print(e - s)
$ python bench2.py 0.48730753067792154 6.189143533993047
perl
$x = 0.5;
for ($i = 0; $i < 1000000000; $i++) {
$x = 1 / ($x * ($x - 1)) + 4.6;
}
print $x;
$ perl --version This is perl 5, version 30, subversion 0 (v5.30.0) built for x86_64-linux-gnu-thread-multi (with 50 registered patches, see perl -V for more detail) Copyright 1987-2019, Larry Wall Perl may be copied only under the terms of either the Artistic License or the GNU General Public License, which may be found in the Perl 5 source kit. Complete documentation for Perl, including FAQ lists, should be found on this system using "man perl" or "perldoc perl". If you have access to the Internet, point your browser at http://www.perl.org/, the Perl Home Page. $ time perl bench.pl 0.487307530677922 real 1m26.594s user 1m25.330s sys 0m0.029s
ruby
x = 0.5 for i in 1..1000000000 x = 1 / (x * (x - 1)) + 4.6 end print x, "\n"
$ ruby --version ruby 2.7.0p0 (2019-12-25 revision 647ee6f091) [x86_64-linux-gnu] $ time ruby bench.rb 0.48730753067792154 real 1m13.829s user 1m12.629s sys 0m0.052s
lua
最小限の仕様でどこまでまともな言語にできるかを追求したような、地味に好きな言語。
x = 0.5
for i=1,1000000000 do
x = 1 / (x * (x - 1)) + 4.6
end
print(x)
$ lua -v Lua 5.3.3 Copyright (C) 1994-2016 Lua.org, PUC-Rio $ time lua bench.lua 0.48730753067792 real 0m36.561s user 0m36.033s sys 0m0.009s
luajit
luaにはluajitという高速実装がある。$ luajit -v LuaJIT 2.1.0-beta3 -- Copyright (C) 2005-2017 Mike Pall. http://luajit.org/ $ time luajit bench.lua 0.48730753067792 real 0m5.958s user 0m5.863s sys 0m0.001s
awk
BEGIN {
x = 0.5;
for (i=1; i<=1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
print x;
}
$ awk --version GNU Awk 5.0.1, API: 2.0 (GNU MPFR 4.0.2, GNU MP 6.2.0) Copyright (C) 1989, 1991-2019 Free Software Foundation. This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/. $ time awk -f bench.awk 0.487308 real 1m37.501s user 1m35.837s sys 0m0.095s
php
<?php
$x = 0.5;
for ($i=1; $i<=1000000000; $i++) {
$x = 1/($x * ($x - 1)) + 4.6;
}
echo $x, "\n";
?>
$ php --version
PHP 7.4.3 (cli) (built: Oct 25 2021 18:20:54) ( NTS )
Copyright (c) The PHP Group
Zend Engine v3.4.0, Copyright (c) Zend Technologies
with Zend OPcache v7.4.3, Copyright (c), by Zend Technologies
$ time php bench.php
0.48730753067792
real 0m16.971s
user 0m16.491s
sys 0m0.048s
octave
いくらなんでも遅すぎ?1; function x = hoge(x) for i=1:1000000000 x = 1 / (x*(x-1)) +4.6; end end tic; x = hoge(0.5); toc x
$ octave --version GNU Octave, version 5.2.0 Copyright (C) 2020 John W. Eaton and others. This is free software; see the source code for copying conditions. There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. Octave was configured for "x86_64-pc-linux-gnu". Additional information about Octave is available at https://www.octave.org. Please contribute if you find this software useful. For more information, visit https://www.octave.org/get-involved.html Read https://www.octave.org/bugs.html to learn how to submit bug reports. $ octave bench.m Elapsed time is 1434.74 seconds. x = 0.48731
いろんな言語でベンチマークまとめ
- IEEE754には従っているようで、試したすべての言語で同じ結果が得られた。
- コンパイラ言語、もしくはJITありのインタプリタは大体6秒前後。
- JITなしのインタプリタは千差万別。地味にphpが速い、次にlua、有名インタプリタ勢は大体1分強。octaveはなにかおかしい。
| 言語 | 計算時間(秒) |
|---|---|
| C++(gcc) | 5.964 |
| C++(clang) | 5.859 |
| Java | 5.941 |
| fortran | 6.045 |
| nim | 5.912 |
| julia | 6.103 |
| python | 75.23 |
| python+numba | 6.189 |
| perl | 85.33 |
| ruby | 72.63 |
| lua | 36.03 |
| luajit | 5.863 |
| awk | 95.84 |
| php | 16.49 |
| octave | 1435 |
倍精度以外で計算させてみる
今度は言語はC++(gcc)に固定し、計算精度を倍精度(double)から他のものに変えて計算時間を測ってみます。むしろこっちに興味がある人もいることでしょう。単精度(float)
倍精度と変わらないかとも思いましたが、少し速くなるようです。
#include <iostream>
int main()
{
int i;
float x;
x = 0.5f; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1.0f / (x * (x - 1.0f)) + 4.6f;
}
std::cout << x << std::endl;
}
$ c++ -O3 float32.cc $ time ./a.out 0.596567 real 0m5.460s user 0m5.371s sys 0m0.004s
Intelの80bit拡張倍精度
SSE等のSIMD命令が出てくる前のIntel CPUで主に使われていたFPUの演算器は、全長80bit、仮数部64bitの拡張倍精度を持っています。今どきのx86_64向けのバイナリーではFPUを使うことはなく、盲腸のような存在ですが、頑張って使おうと思えば使うことが出来ます。ただし、今のMSVCでは使うのは難しいです。詳細は省きますが、gccやclangでは使うことができて、math.hまたはcmathをincludeした上で_Float64xという型名で使うのが一番良さそうです。
#include <iostream>
#include <cmath>
int main()
{
int i;
_Float64x x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float64x.cc $ time ./a.out 0.447779 real 0m6.436s user 0m6.325s sys 0m0.008sこの並列性が生かせない特殊なベンチマークのためだとは思いますが、倍精度と遜色ない速度が出ているのは少し驚きです。
double-double (qdライブラリ)
倍精度浮動小数点数を2つ使って、擬似的に106bit相当の仮数部を持つ4倍精度数を作る方法があります。double-doubleとか、縮めてddとか呼ばれます。Baileyによるqdライブラリがよく知られています。qdは、倍精度を4つ使うquad-doubleと2つ使うdouble-doubleの演算ができますが、今回はdouble-doubleの方を試してみました。sudo apt install qd-devでインストールしたものを使いました。
#include <iostream>
#include <qd/qd_real.h>
int main()
{
unsigned int oldcw;
fpu_fix_start(&oldcw);
int i;
dd_real x;
x = 0.5;
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << "\n";
fpu_fix_end(&oldcw);
}
$ c++ -O3 qd.cc -lqd $ time ./a.out 5.343242e-01 real 0m48.568s user 0m48.047s sys 0m0.008s
double-double (kvライブラリ)
私が作っている精度保証付き数値計算のためのライブラリkvにも、double-double数が実装されているので、その計算時間も計測してみました。
#include <kv/dd.hpp>
int main()
{
int i;
kv::dd x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 dd.cc $ time ./a.out 0.599108 real 0m37.365s user 0m36.737s sys 0m0.012s $ c++ -O3 -DKV_USE_TPFMA dd.cc $ time ./a.out 0.599108 real 0m30.161s user 0m29.656s sys 0m0.009sFMA非使用とFMA使用の両方でコンパイルしてみました。どちらでもqdより速いのは意外だったけど、嬉しいですね!
float128
IEEE754-2008で規格化された、全長128bit、仮数部113bitの浮動小数点形式です。残念ながらハードウェアでサポートしているCPUはほとんどありません。gccではlibquadmathで実装されたソフトウェアエミュレーションを使うことができます。cout等を使って楽をしたかったので、このサンプルではboost::multiprecisionを通じて使用しています。
#include <iostream>
#include <boost/multiprecision/float128.hpp>
int main()
{
int i;
boost::multiprecision::float128 x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
$ c++ -O3 float128.cc -lquadmath $ time ./a.out 0.547514 real 1m41.450s user 1m39.683s sys 0m0.028sソフトウェアエミュレーションにしては速い印象です。よほどすごい人が書いたのでしょうか。
mpfr
mpfrは有名なライブラリで、任意の仮数部長の浮動小数点演算を行うことができます。kvライブラリのmpfrラッパー機能を使って、53bit, 64bit, 106bit, 113bitの浮動小数点演算の速度を計測してみました。mpfrは、sudo apt install mpfr-devで入れたものです。
#include <kv/mpfr.hpp>
int main()
{
int i;
kv::mpfr<53> x;
x = 0.5; // 0.4 < x < 0.6
for (i=0; i<1000000000; i++) {
x = 1 / (x * (x - 1)) + 4.6;
}
std::cout << x << std::endl;
}
このプログラム中の53の部分を変えながら計測してみました。$ c++ -O3 mpfr53.cc -lmpfr $ time ./a.out 0.487308 real 3m54.608s user 3m50.821s sys 0m0.044s $ c++ -O3 mpfr64.cc -lmpfr $ time ./a.out 0.447779 real 5m16.806s user 5m11.236s sys 0m0.111s $ c++ -O3 mpfr106.cc -lmpfr $ time ./a.out 0.576081 real 5m37.827s user 5m32.035s sys 0m0.111s $ c++ -O3 mpfr113.cc -lmpfr $ time ./a.out 0.547514 real 5m42.499s user 5m36.300s sys 0m0.241smpfrは、多倍長演算のプログラムとしては十分高速で定評がありますが、さすがに遅いですね。
倍精度以外の計算速度まとめ
| 数値型 | 計算時間(秒) |
|---|---|
| 単精度 (全長32bit, 仮数部24bit) | 5.371 |
| 倍精度 (全長64bit, 仮数部53bit) | 5.964 |
| Intel拡張倍精度 (全長80bit, 仮数部64bit) | 6.325 |
| double-double by qd (全長128bit, 仮数部106bit相当) | 48.05 |
| double-double by kv (全長128bit, 仮数部106bit相当) | 36.74 |
| double-double by kv with FMA (全長128bit, 仮数部106bit相当) | 29.66 |
| float128 (全長128bit, 仮数部113bit) | 99.68 |
| mpfr (仮数部53bit) | 230.8 |
| mpfr (仮数部64bit) | 311.2 |
| mpfr (仮数部106bit) | 332.0 |
| mpfr (仮数部113bit) | 336.3 |
変なベンチマークの力学系的性質
ここからはオマケです。一応、この反復式
x_{n+1} = \frac{1}{x_n(x_n-1)} + 4.6
をどうやって作ったのか種明かしをしておきましょう。区間[0.4,0.6]でこの右辺のグラフを書くと、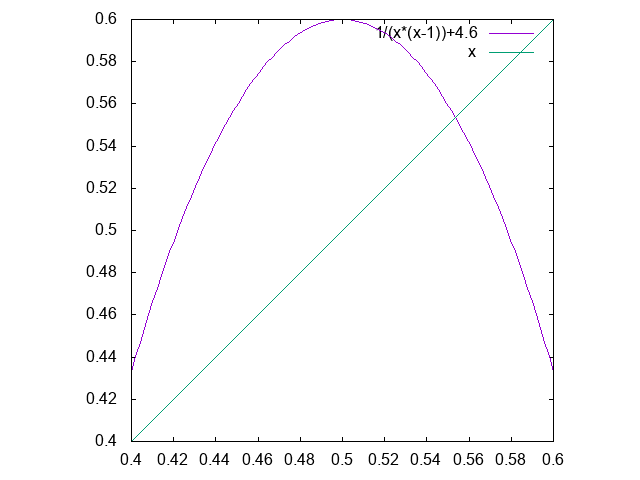
のようになります。すなわち、区間[0.4,0.6]から区間[0.4,0.6]への写像で、いわゆるロジスティック写像に形を似せて、カオスの発生を期待しました。
これが本当にカオスになっているのか自分の知識ではよく分かりませんが、安定な不動点、あるいは安定なn周期点があるとそこに吸い込まれてしまうので、それらが不安定である必要があります。不動点~5周期点までを探索してその安定性を調べてみたら、
| 周期点 | 傾き |
|---|---|
| 不動点 | |
| [0.55356306259771814,0.55356306259771904] | [-1.7540458821004337,-1.7540458821003905] |
| 2周期点 | |
| [0.47251229982482656,0.47251229982483978] | [-2.6496000000100227,-2.6495999999899826] |
| [0.58787417360511429,0.58787417360512307] | [-2.649600000013118,-2.6495999999869042] |
| 4周期点 | |
| [0.45660292682622499,0.45660292682782184] | [-6.994344006430338,-6.9943413287099849] |
| [0.56963838378845921,0.56963838379004439] | [-6.9943442880413019,-6.994341047098123] |
| [0.52087302149875114,0.52087302149987225] | [-6.9943435009524846,-6.9943418341871632] |
| [0.59301690190605937,0.59301690190710344] | [-6.9943446375696477,-6.9943406975699096] |
| 5周期点1 | |
| [0.49241639587271796,0.49241639589626041] | [-5.3195999647673152,-5.3191146240917346] |
| [0.59907961143524002,0.59907961146046785] | [-5.3210234368141052,-5.3176911750450219] |
| [0.43651199326412942,0.43651199328730845] | [-5.319869439031236,-5.3188451535460181] |
| [0.53445153616664387,0.5344515362008826] | [-5.3198513032572504,-5.3188632923945835] |
| [0.58091887627954896,0.58091887630723616] | [-5.3198877237365352,-5.3188268706445134] |
| 5周期点2 | |
| [0.43930700020768825,0.4393070002409904] | [7.3230674094215144,7.3246535122595358] |
| [0.54018034001802039,0.54018034004123794] | [7.3234484071188221,7.3242725048956273] |
| [0.57400074538735523,0.57400074542057201] | [7.3231434952559464,7.3245774251428078] |
| [0.51042003579714645,0.51042003582068152] | [7.3235356733528114,7.3241852373848194] |
| [0.59826201082553276,0.59826201084694897] | [7.3224303075700802,7.3252906173775747] |
2017/08/31(木)C++で気軽にリアルタイムグラフ表示 (matplotlib.hpp)
動機
日頃、C++でいろいろ計算していて、計算結果をグラフにしたいことがよくあります。テキストで吐かせて、必要ならば加工して、gnuplotで表示というのが定番でしょうか。最近はpythonで動くmatplotlibを使うことも多いです。計算が終わってからグラフにするならこれでいいのでしょうが、計算中に現在の状況をリアルタイムに見たい、ということもあります。30年前のBASICの時代なら、LINE (0,0)-(639,399)とかすればすぐに画面に線が出たので、こういうのがとても気軽に出来ましたが、今はなかなか面倒な気がします。誰もがOpenGLでさっと書ける、というわけにはいかないでしょう。
これを実現する方法として、あまり知られていませんがgnuplotをパイプで繋いでリアルタイム描画させる方法があります。例えば、「C言語でgnuplotを利用してグラフ表示」に例があります。kvライブラリにもひっそりとgnuplotを使ったライブラリが含まれています。しかし、この方法は描画するオブジェクトが増えると非常に遅くなってしまい、実用的とは言い難いものでした。
gnuplotでなくmatplotlibならいくらか速そうなので、それで出来ないかと以前から考えていました。で、pythonインタプリタをパイプで繋いでpythonコマンドを文字列で送り込む作戦で作ってみました。作ってみたら案外良さそうなので記事にしました。kvライブラリにも入れようかな。
プログラム
作ったファイルは一つ(matplotlib.hpp)です。
#ifndef MATPLOTLIB_HPP
#define MATPLOTLIB_HPP
#include <cstdio>
class matplotlib {
FILE *p;
public:
bool open() {
p = popen("python -c 'import code; import os; import sys; sys.stdout = sys.stderr = open(os.devnull, \"w\"); code.InteractiveConsole().interact()'", "w");
if (p == NULL) return false;
send_command("import matplotlib.pyplot as plt");
send_command("import matplotlib.patches as patches");
send_command("fig, ax = plt.subplots()");
send_command("plt.show(block=False)");
return true;
}
bool close() {
send_command("plt.close()");
send_command("quit()");
if (pclose(p) == -1) return false;
return true;
}
void screen(double x1, double y1, double x2, double y2, bool EqualAspect = false) const {
if (EqualAspect == true) {
fprintf(p, "ax.set_aspect('equal')\n");
}
fprintf(p, "plt.xlim([%.17f,%.17f])\n", x1, x2);
fprintf(p, "plt.ylim([%.17f,%.17f])\n", y1, y2);
fprintf(p, "plt.draw()\n");
fflush(p);
}
void line(double x1, double y1, double x2, double y2, const char *color = "blue", const char *opt = "") const {
fprintf(p, "ax.draw_artist(ax.plot([%.17f,%.17f],[%.17f,%.17f], color='%s', %s)[0])\n", x1, x2, y1, y2, color, opt);
fprintf(p, "fig.canvas.blit(ax.bbox)\n");
fprintf(p, "fig.canvas.flush_events()\n");
fflush(p);
}
void point(double x, double y, const char *color = "blue", const char *opt = "") const {
fprintf(p, "ax.draw_artist(ax.scatter([%.17f],[%.17f], color='%s', %s))\n", x, y, color, opt);
fprintf(p, "fig.canvas.blit(ax.bbox)\n");
fprintf(p, "fig.canvas.flush_events()\n");
fflush(p);
}
void rect(double x1, double y1, double x2, double y2, const char *edgecolor = "blue", const char *facecolor = NULL, const char *opt = "") const {
if (facecolor == NULL) {
fprintf(p, "ax.draw_artist(ax.add_patch(patches.Rectangle(xy=(%.17f,%.17f), width=%.17f, height=%.17f, fill=False, edgecolor='%s', %s)))\n", x1, y1, x2-x1, y2-y1, edgecolor, opt);
} else {
fprintf(p, "ax.draw_artist(ax.add_patch(patches.Rectangle(xy=(%.17f,%.17f), width=%.17f, height=%.17f, fill=True, edgecolor='%s', facecolor='%s', %s)))\n", x1, y1, x2-x1, y2-y1, edgecolor, facecolor, opt);
}
fprintf(p, "fig.canvas.blit(ax.bbox)\n");
fprintf(p, "fig.canvas.flush_events()\n");
fflush(p);
}
void ellipse(double cx, double cy, double rx, double ry, const char *edgecolor = "blue", const char *facecolor = NULL, const char *opt = "") const {
if (facecolor == NULL) {
fprintf(p, "ax.draw_artist(ax.add_patch(patches.Ellipse(xy=(%.17f,%.17f), width=%.17f, height=%.17f, fill=False, edgecolor='%s', %s)))\n", cx, cy, rx*2, ry*2, edgecolor, opt);
} else {
fprintf(p, "ax.draw_artist(ax.add_patch(patches.Ellipse(xy=(%.17f,%.17f), width=%.17f, height=%.17f, fill=true, edgecolor='%s', facecolor='%s', %s)))\n", cx, cy, rx*2, ry*2, edgecolor, facecolor, opt);
}
fprintf(p, "fig.canvas.blit(ax.bbox)\n");
fprintf(p, "fig.canvas.flush_events()\n");
fflush(p);
}
void circle(double cx, double cy, double r, const char *edgecolor = "blue", const char *facecolor = NULL, const char *opt = "") const {
ellipse(cx, cy, r, r, edgecolor, facecolor, opt);
}
void polygon(double *x, double *y, int n, const char *edgecolor = "blue", const char *facecolor = NULL, const char *opt = "") const {
int i;
fprintf(p, "ax.draw_artist(ax.add_patch(patches.Polygon((");
for (i=0; i<n; i++) {
fprintf(p, "(%.17f,%.17f),", x[i], y[i]);
}
if (facecolor == NULL) {
fprintf(p, "), fill=False, edgecolor='%s', %s)))\n", edgecolor, opt);
} else {
fprintf(p, "), fill=True, edgecolor='%s', facecolor='%s', %s)))\n", edgecolor, facecolor, opt);
}
fprintf(p, "fig.canvas.blit(ax.bbox)\n");
fprintf(p, "fig.canvas.flush_events()\n");
fflush(p);
}
void save(const char *filename) const {
fprintf(p, "plt.savefig('%s')\n", filename);
fflush(p);
}
void send_command(const char *s) const {
fprintf(p, "%s\n", s);
fflush(p);
}
void clear() const {
send_command("plt.clf()");
}
};
#endif // MATPLOTLIB_HPP
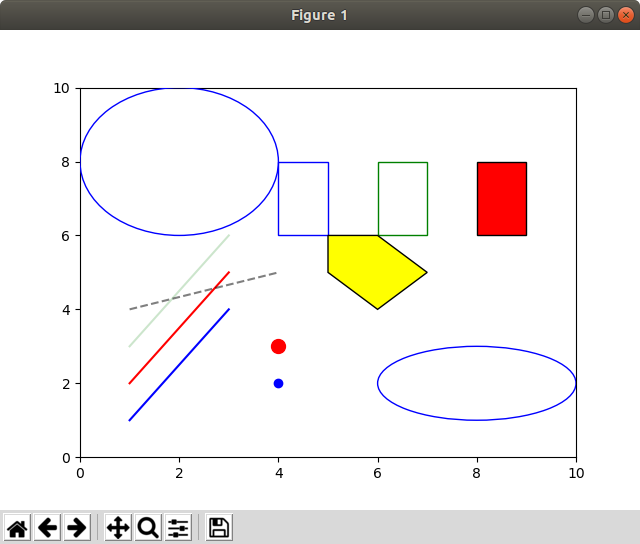
以下は簡単なテストプログラム(test-matplotlib.cc)。
#include "matplotlib.hpp"
int main()
{
matplotlib g;
// initialize
g.open();
// set drawing range
g.screen(0, 0, 10, 10);
// aspect ratio = 1
// g.screen(0, 0, 10, 10, true);
g.line(1,1,3,4);
g.line(1,2,3,5, "red");
g.rect(4,6,5,8);
g.rect(6,6,7,8, "green");
g.rect(8,6,9,8, "black", "red");
g.point(4,2);
g.ellipse(8,2,2,1);
g.circle(2,8,2);
double xs[5] = {6., 7., 6., 5., 5.};
double ys[5] = {4., 5., 6., 6., 5.};
g.polygon(xs, ys, 5, "black", "yellow");
g.line(1,3,3,6, "green", "alpha=0.2");
g.line(1,4,4,5, "black", "alpha=0.5, linestyle='--'");
g.point(4, 3, "red", "s=100");
g.save("test.pdf");
getchar();
// finish drawing
g.close();
}
普通にコンパイルして走らせると、matplotlibが使えるpythonがインストールされていれば、のように表示されます。非常に短いプログラムなのでソースを見るのが早いような気もしますが、以下、簡単に使い方を説明します。
基本
#include "matplotlib.hpp"
int main()
{
matplotlib g;
g.open();
g.close();
}
これが最小限でしょうか。matplotlib.hppをインクルードし、matplotlibオブジェクトgを一つ作り、g.open()でウィンドウが開き、gに対していろいろ描画命令を発行し、g.close()でウィンドウを閉じます。描画範囲
g.screen(0, 0, 10, 10);で、描画範囲を(x,y)=(0,0)と(x,y)=(10,10)を対角線とする領域に設定しています。
g.screen(0, 0, 10, 10, true);のようにすると、x座標とy座標のアスペクト比が1になります(正方形が正方形に描画される)。
線分
g.line(1,1,3,4);のようにすると点(1,1)から点(3,4)へ線分が引かれます。
g.line(1,2,3,5, "red");のように色を指定することも出来ます。色の指定方法は、"Specifying Colors"で詳細を見ることが出来ます。
長方形
g.rect(4,6,5,8);で、点(4,6)、点(5,8)を対角線とする長方形が描かれます。線分と同様に、
g.rect(6,6,7,8, "green");で色を指定できます。
g.rect(8,6,9,8, "black", "red");のように色を2つ指定すると、一つ目の色で枠線が描かれ、二つ目の色で中が塗りつぶされます。
点
g.point(4,2);(4,2)に点が打たれます。線分と同様に色を付けることも出来ます。
楕円
g.ellipse(8,2,2,1);中心が(8,2)、x方向の半径が2、y方向の半径が1であるような楕円を描画しています。長方形と同様に色を付けたり塗りつぶしたり出来ます。
円
g.circle(2,8,2);中心が(2,8)、半径が2の円を描画しています。長方形と同様に色を付けたり塗りつぶしたり出来ます。
多角形
double xs[5] = {6., 7., 6., 5., 5.};
double ys[5] = {4., 5., 6., 6., 5.};
g.polygon(xs, ys, 5, "black", "yellow");
点(6,4),(7,5),(6,6),(5,6),(5,5)をこの順に結んだ五角形を表示しています。長方形と同様に色を付けたり塗りつぶしたり出来ます。ファイルにセーブ
g.save("test.pdf");
このように、その時点での画像をファイルにセーブできます。ファイル形式は拡張子で指定します。画面消去
g.clear()で画面消去できます。座標系の設定もクリアされるようで、g.screen()からやり直す必要がありそう。追加オプション
g.line(1,3,3,6, "green", "alpha=0.2"); g.line(1,4,4,5, "black", "alpha=0.5, linestyle='--'"); g.point(4, 3, "red", "s=100");matplotlibには、線の種類や線の太さなど、更に無数のオプションがあります。それらを全て引数として用意するのは面倒だったので、最後の引数に文字列で書くとそれがそのままmatplotlibの該当コマンドのオプションとして渡されるようにしました。上の例は、
- alpha=0.2として薄く表示
- alpha=0.5として、更に線種を変更
- 点を大きく
技術的な細かいこと
- 最初にpopenしてるところ、単にpythonインタプリタを呼ぶのでなく妙な引数がついてますが、自分の環境ではpythonインタプリタをそのまま呼んだ場合標準入力を一行ずつ読んでくれなかったので、小細工しました。もっとスマートな方法募集中です。
- 普通に書くと新しく何かを描画する毎に全体を再描画してしまいgnuplotと同様遅くなってしまったので、blittingとかいう技を使って再描画を抑制しているつもりです。しかし、matplotlibの構造を全く知らずに適当に実験しながら作ったので、とんでもなく的外れなことをしているかもしれません。
- C++とlibpythonをリンクしてpythonインタプリタ自身をプログラム中に取り込んでしまう方法でも同じことが出来ます。しかし、コンパイル時のオプションが必要だったり気軽さが失われてしまうのと、描画の重さに比べてパイプのオーバーヘッドはあまり大きく無さそうなので、気軽なパイプで作ってみました。
オマケ
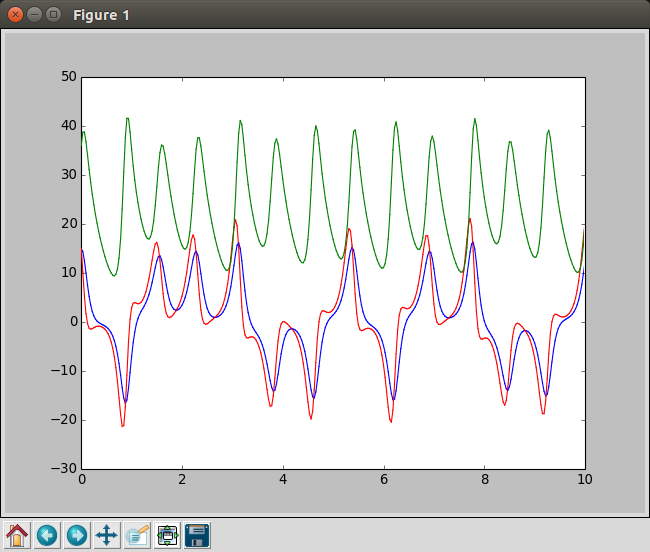
最後にオマケでLorezn方程式の初期値問題の解を計算しながら描画する例です。boost.ublasを使っています。
#include <boost/numeric/ublas/vector.hpp>
#include "matplotlib.hpp"
namespace ub = boost::numeric::ublas;
template <class T, class F>
void rk(F f, ub::vector<T>& init, T start, T end) {
ub::vector<T> x, dx1, dx2, dx3, dx4, x1, x2, x3;
T t = start;
T dt = end - start;
x = init;
dx1 = f(x, t) * dt;
x1 = x + dx1 / 2.;
dx2 = f(x1, t + dt/2.) * dt;
x2 = x + dx2 / 2.;
dx3 = f(x2, t + dt/2.) * dt;
x3 = x + dx3;
dx4 = f(x3, t + dt) * dt;
init = x + dx1 / 6. + dx2 / 3. + dx3 / 3. + dx4 / 6.;
}
struct Lorenz {
template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
ub::vector<T> y(3);
y(0) = 10. * ( x(1) - x(0) );
y(1) = 28. * x(0) - x(1) - x(0) * x(2);
y(2) = (-8./3.) * x(2) + x(0) * x(1);
return y;
}
};
int main()
{
int i, j;
ub::vector<double> x, x_new;
double t, t_new, dt;
const char *colors[3] = {"blue", "red", "green"};
matplotlib g;
g.open();
g.screen(0., -30., 10., 50.);
x.resize(3);
x(0) = 15.; x(1) = 15.; x(2) = 36.;
t = 0.;
dt = pow(2., -5);
for (i=0; i < (1 << 5) * 10; i++) {
x_new = x;
t_new = t + dt;
rk(Lorenz(), x_new, t, t_new);
for (j=0; j<3; j++) {
g.line(t, x[j], t_new, x_new[j], colors[j]);
}
x = x_new;
t = t_new;
}
getchar();
g.close();
}
これを実行すると、のようなグラフが計算しながら描かれます。
おわりに
短いのでコピペでも十分でしょうけど、ここに載せた3つのプログラムをzipであげておきます。matplotlib.zip
見れば分かるように単純なことしかしていませんので、C++以外の他の言語でも似たようなことは簡単に出来ると思います。
お役に立てば幸いです。
2019年4月10日追記
rectがバグっていたので直しました。2017/04/17(月)bash on Ubuntu on Windowsで遊んでみる (Creators Update編)
前回(Anniversary Update時)との差分は、
- ubuntuのバージョンが14.04から16.04になった。
- ターミナルが改善し、日本語が文字化けせずきちんと扱えるようになった。WindowsのIMEでの日本語入力も可能に。
- ubuntuからwindows内のコマンドを呼び出したり、windowsからubuntu内のコマンドを呼び出したりできるようになった。
- ifconfigやpingなどのネットワーク系のコマンドが動作するようになった。
条件はWindows10の64bitで、Creators Updateになっていることです。「スタート→歯車アイコン→システム→バージョン情報」で
のようにバージョンが1703になっていればCreators Updateになっています。まだだった場合でも強制的にアップデートすることもできます。
インストール方法は前回とほとんど変わっていませんが一応書いておきます。
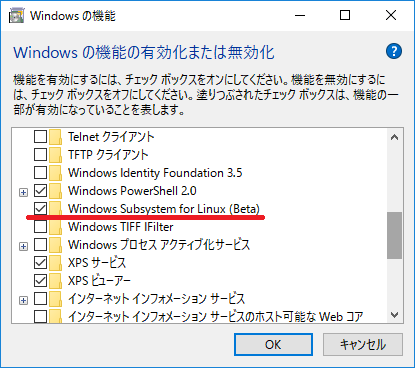
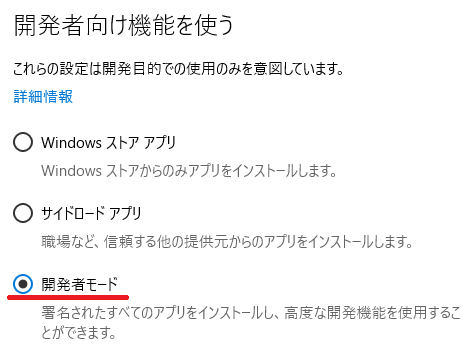
- 「スタート→歯車アイコン→アプリ→プログラムと機能→Windowsの機能の有効化または無効化」で、「Windows Subsysyem for Linux (Beta)」をチェックする。再起動。

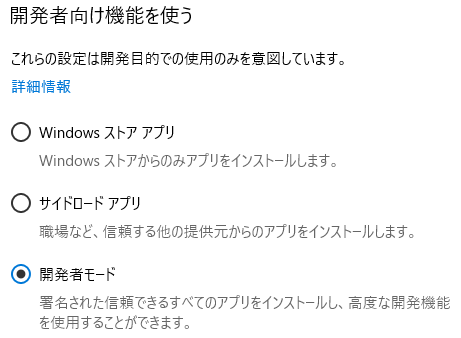
- 「スタート→歯車アイコン→更新とセキュリティ→開発者向け」で、「開発者モードを使う」を、「サイドロードアプリ」から「開発者モード」に変更。再起動。
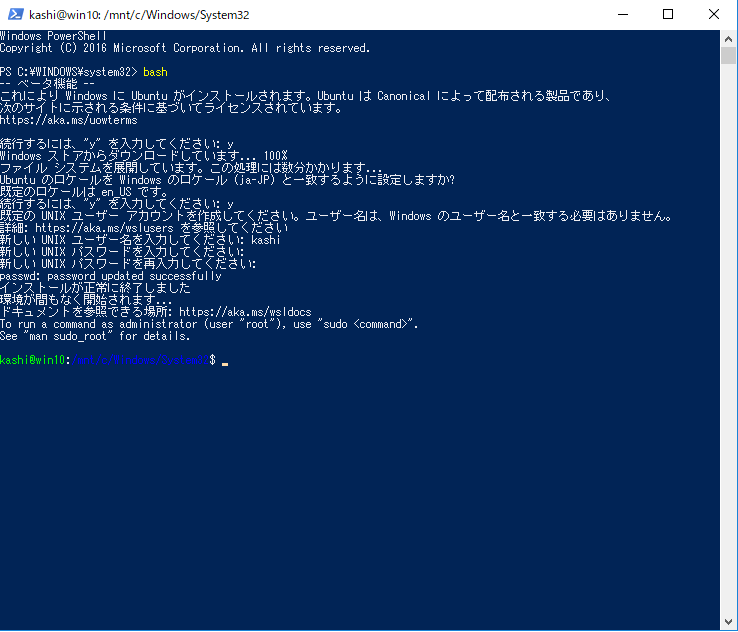
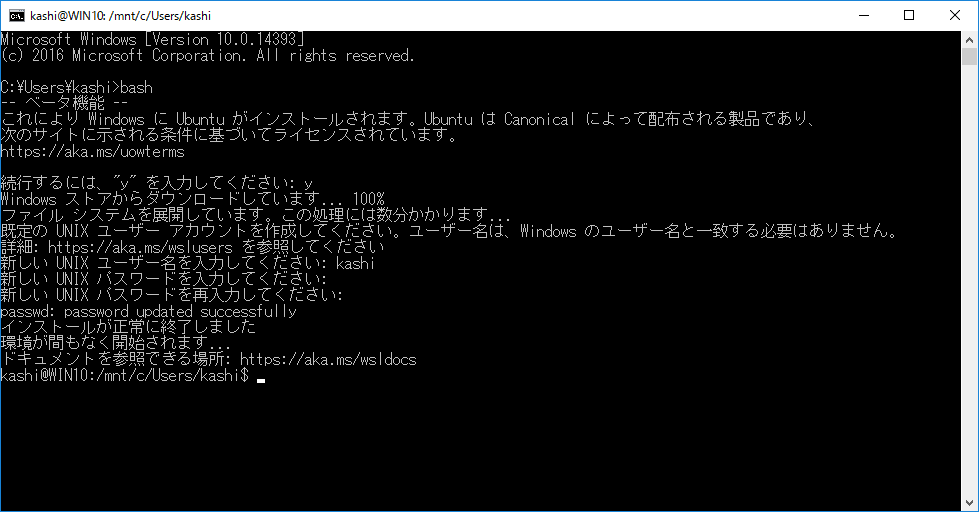
- 「スタートを右クリック→Windows PowerShell(管理者)」でPower Shellを起動し、bashとタイプ。"y"でダウンロードとインストールが始まります。数分かかります。ユーザIDとパスワードを聞かれてインストール完了。ここで入れたパスワードは"sudo"実行時に使います。
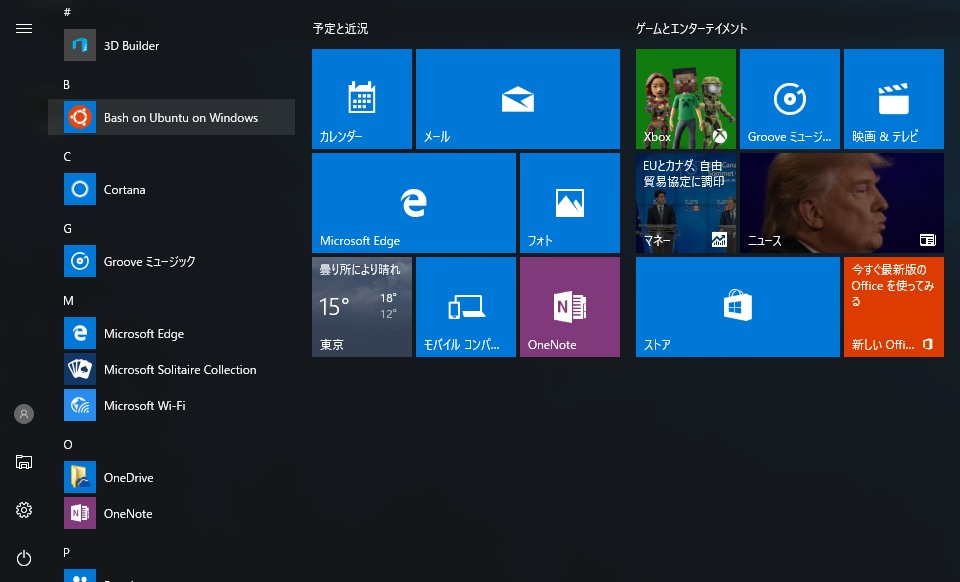
- 次回以降は、スタートメニューに「Bash on Ubuntu on Windows」が登録されているのでそこから起動できます。
lxrun /uninstall /fullで全削除し、「bashとタイプ」のところからやりなおすのが確実です。
使い方は、前回のAnniversary Updateのときとほとんど変わっていません。日本語が文字化けしなくなり、またターミナルからwindowsのIMEを使って日本語入力ができるようになったので、ちょっとしたプログラミングの演習程度ならこのままで十分に使えるようになりました。
また、X serverをwindowsに入れてGUIを使うソフトウェアを動かすこともできます。bash on ubuntu on windowsで遊んでみるの記事で紹介した
- gnuplot
- firefox
- lxterminal
- Xアプリでの日本語入力
- tex
2016/10/31(月)bash on Ubuntu on Windowsを試してみる
cygwinやmsys2など、Windows上でunixツールを使うためのものは以前からいろいろありますが、Microsoft本家が出してきたこいつは、「ubuntuのバイナリがそのまま動く」という点が今までと違います。使うための条件は、
- Windows10の64bit版であること
- Windows10のバージョン1607以降であること
8月のリリース以降、少しずつ時間をずらしながらWindows Updateを降らせていたようですが、そろそろほとんどのWindows10が1607になった頃ではないでしょうか。
インストール
インストール方法の情報は検索すればたくさん出てきますが、次のような手順です。- 「スタートを右クリック→プログラムと機能→Windowsの機能の有効化または無効化」で、「Windows Subsysyem for Linux (Beta)」をチェックする。再起動。
- 「スタート→歯車アイコン→更新とセキュリティ→開発者向け」で、「開発者モードを使う」を、「サイドロードアプリ」から「開発者モード」に変更。再起動。
- 「スタートを右クリック→コマンドプロンプト」でコマンドプロンプトを起動し、bashとタイプ。"y"でダウンロードとインストールが始まります。数分かかります。ユーザIDとパスワードを聞かれてインストール完了。
- 次回以降は、スタートメニューに「Bash on Ubuntu on Windows」が登録されているのでそこから起動できます。
アンインストール
いろいろ試しにパッケージを入れたりしてシステムが壊れることもあるかと思いますが、コマンドプロンプトでlxrun /uninstall /fullと入れるときれいさっぱり削除できます。上の「bashとタイプ」のところからやりなおすことが出来ます。
簡単な使い方など
- 中身はubuntu 14.04です。いつものubuntuの作法通り、
sudo apt update sudo apt upgrade
で最新に更新しておきましょう。 - これで、端末内で完結するような作業は大体できます。最初は最低限しかインストールされていないので、いつものubuntuの作法で必要なパッケージをインストールしましょう。とりあえず
sudo apt install build-essential
でCコンパイラなど最低限の開発環境を入れることをお勧めします。 - ubuntu側からは、windows側のファイルが例えばCドライブなら
/mnt/c/
以下に見えます。逆にwindows側から見てubuntuのファイルシステムは
c:\Users\(windowsユーザ名)\AppData\Local\lxss\
にあり、このフォルダがubuntu側の"/"に対応しています。隠しファイルになっているので普通の状態では見えないかも知れません。恐らく、ubuntu側からwindowsのファイルシステムを操作することはOK、windows側からubuntuのファイルシステムを操作するのはNG、だと思われます。
- X windowを使うソフトウェアが動かない。gnuplotくらい使いたい!
- (文字幅を正しく扱えないせいか)日本語が頻繁に文字化けする。
- そもそも日本語が入力できない。
X環境を作る
買ったままのwindowsでソフトウェア追加無しにunix環境が使えるのがbash on ubuntu on windowsのメリットですが、windows用のX serverを入れてしまえば使えるソフトウェアが一気に増え、また日本語の問題も解決できる可能性があります。そこで、上記問題点を解決すべく、X serverを入れてみます。X serverは有料、無料いろいろあると思いますが、いろいろ検索してみると無料では
の2つがよく使われているようです。今回はXmingの方を使ってみました。Xming X Serverによると、Public Domain Releasesという無料版と、Website Releaseという新しいが寄付が必要な版があるようです。今回はPublic Domain Releasesの方を使いました。
- Xming 6.9.0.31
- Xming-fonts 7.7.0.10
スタートメニューから「Xming」を起動します。(「XLaunch」の方だといろいろオプションを設定してから起動します。今回はデフォルトのままで十分。) すると、右下に
のようなアイコンが出ます。これで、bash on ubuntu on windowsからの描画命令を受け止める準備が出来たことになります。動作チェックします。
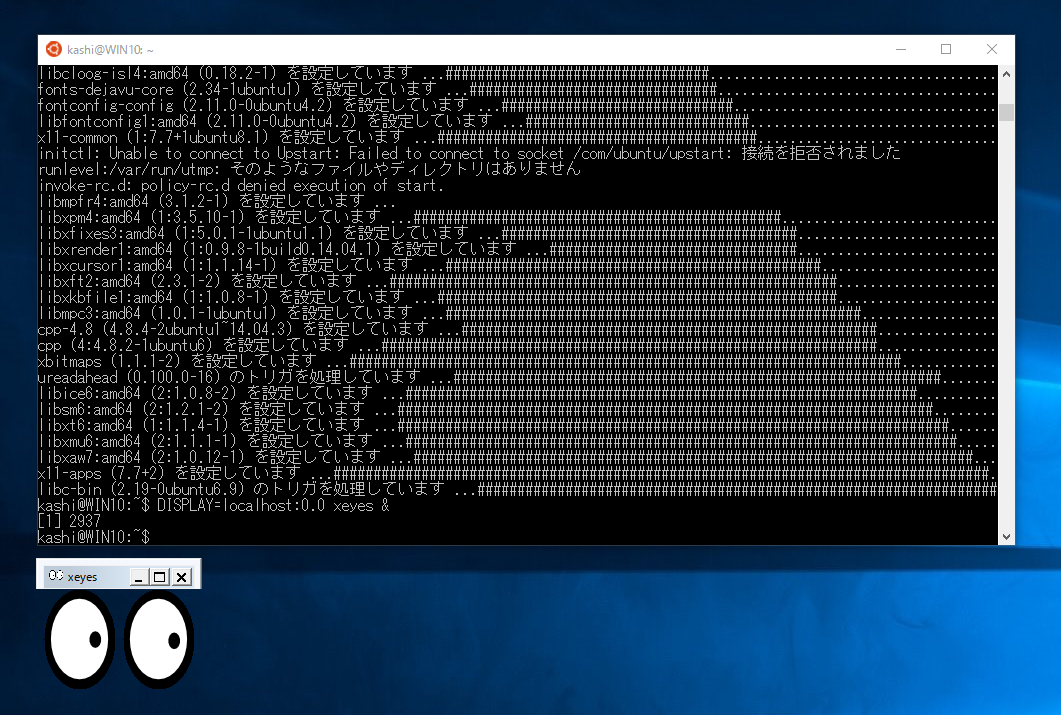
sudo apt install x11-apps sudo apt install x11-utils sudo apt install x11-xserver-utilsといくつかのx11の基本アプリをインストールして、
DISPLAY=localhost:0.0 xeyes &とxeyesを起動してみます。
のようにマウスカーソルを追う目玉が表示されたら、正常に動作しています。
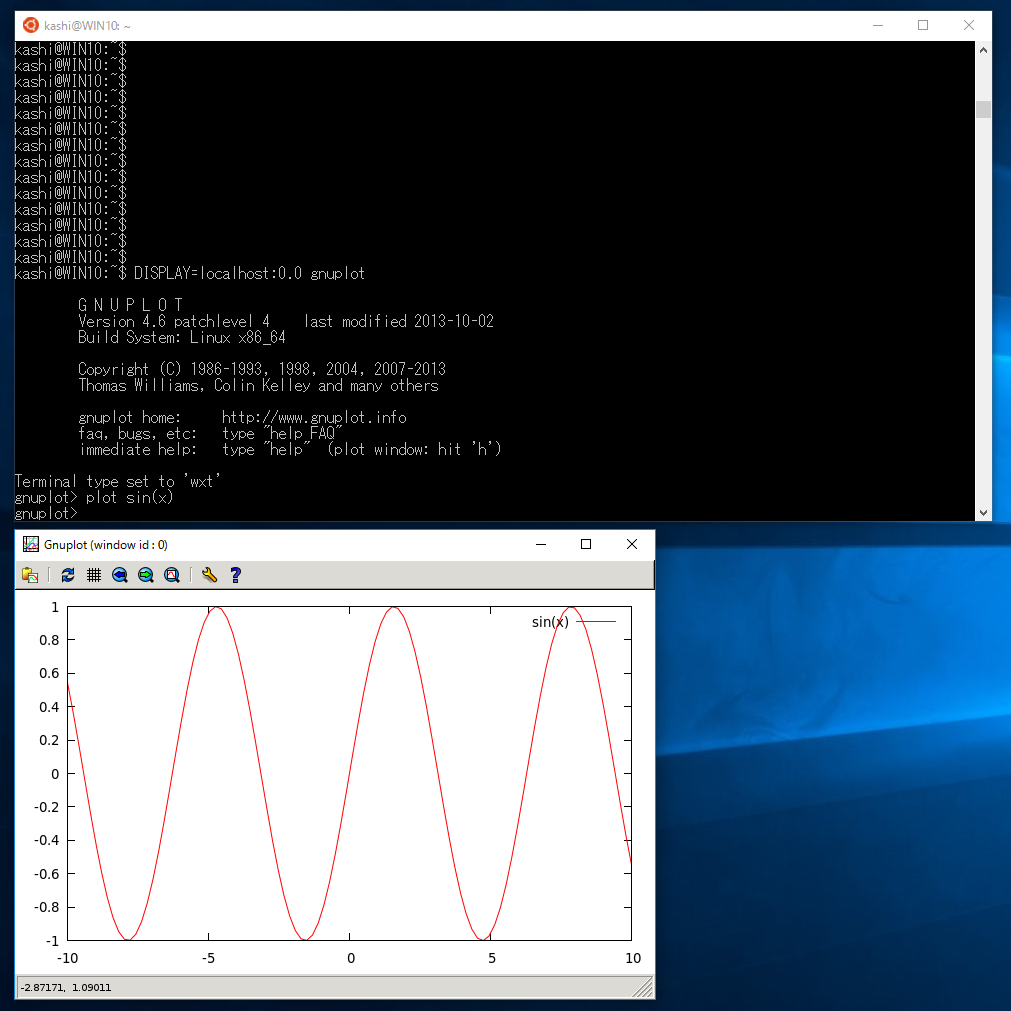
gnuplotを試してみましょう。
sudo apt install gnuplot-x11としてインストールし、
DISPLAY=localhost:0.0 gnuplotとして起動します。
のように、ちゃんと動作しました。毎回「DISPLAY=localhost:0.0」とするのが面倒なら、
export DISPLAY=localhost:0.0とすると、端末を閉じるまで有効になります。
驚くべきことに、日本語フォントを追加してやると、少しエラーが出るもののfirefoxを動かすことができます。
sudo apt install fonts-ipafont sudo apt install firefox
日本語環境を整える
ここまでちゃんと動作するとなると、日本語の読み書きがまともにできないのが惜しくなってきます。そこで、少し頑張って環境を整えてみました。いろいろ試行錯誤した結果ではありますが、もっといい方法もありそうなので情報が欲しいところです。以下、自分が試した方法を書きます。X serverがwindows側にインストールしてあって、また上で書いたように、sudo apt install fonts-ipafontで日本語フォントを追加してあるものとします。
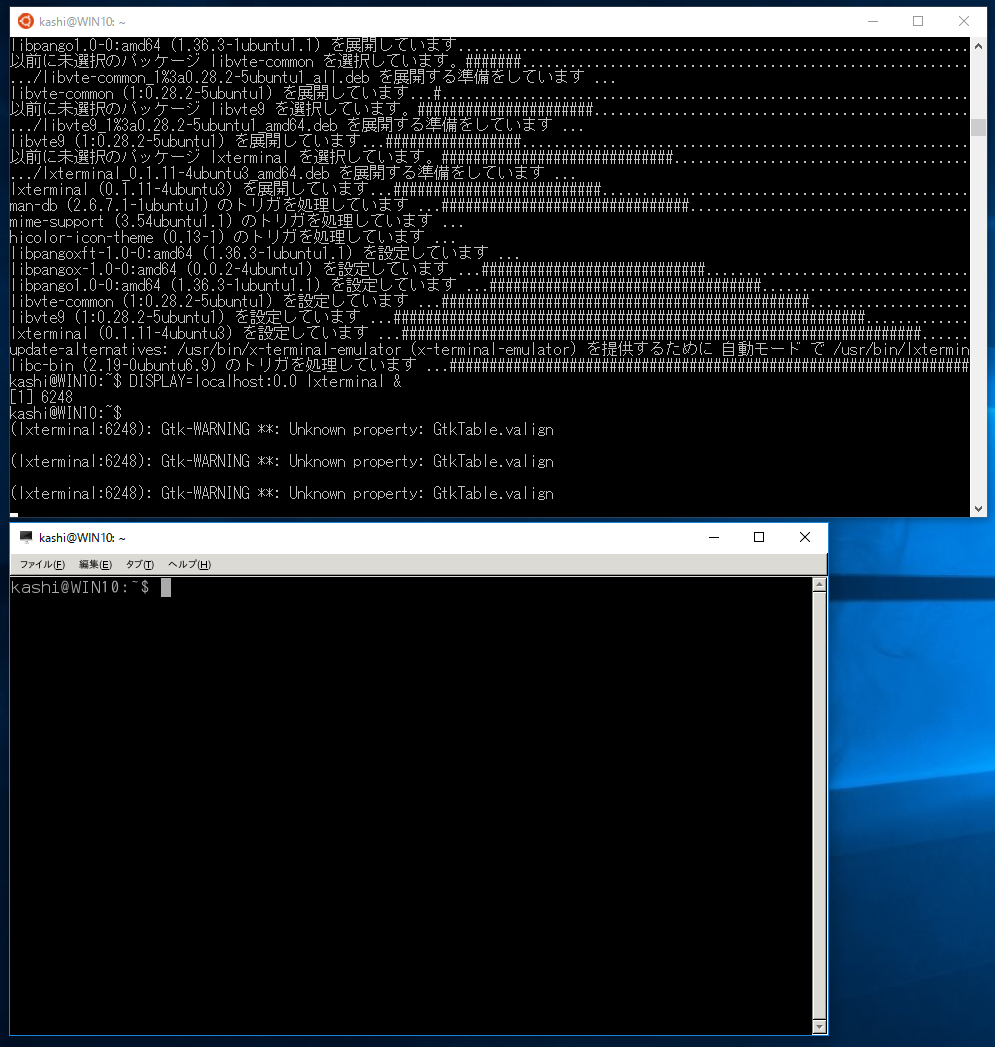
まず、端末は、windows側を捨ててXの方で動かすことにします。いろいろ試しましたが、lxterminalが良さそうでした。
sudo apt install lxterminalでインストールし、
DISPLAY=localhost:0.0 lxterminal &で起動します。起動後に「編集→設定」でフォントをMonoSpace 10からMonospace 15くらいにしてあげると見やすい感じになりました。
windows側の端末を使わずにこちらを使うことにします。こちらからだと「DISPLAY=locahost:0.0」をいちいち打たなくてよくなります。windows側の端末を閉じると全部落ちてしまうので、アイコンにでもしておきましょう。
かな漢字変換のシステムを入れます。いろいろ試しましたが、uim-anthyが何とか動作しました。
sudo apt install uim uim-xim uim-anthyのようにインストールします。そして、windows側のbashターミナルで、
DISPLAY=localhost:0.0 UIM_CANDWIN_PROG=uim-candwin-gtk uim-xim &のようにかな漢字変換サーバを起動し、lxterminalの起動は
DISPLAY=localhost:0.0 XMODIFIERS="@im=uim" GTK_IM_MODULE=uim QT_IM_MODULE=uim lxterminal &とします。これで、「半角/全角」キーで日本語入力ができるようになりました。
terminal起動時の設定が長いですが、このterminalから起動したものにはこの設定が伝わるので、ここからいろいろ起動することにすれば楽です。
その他もろもろ
他にもいろいろ入れてみました。TeX環境。
sudo apt install texlive-lang-cjkで簡単に入ります(ちょっと時間がかかります)。ついでに
sudo apt install evinceでpdfビューアも。
java。
sudo apt install default-jdkあちこちでjavaは動かないという記述を見かけましたが、普通に動いているように見えます。
自分はvimで十分ですが、もう少し普通のエディタを使いたいなら、
sudo apt install geanyあたりはいかがでしょうか。
ま、windows側のお気に入りのエディタを使えば済むことではありますが。
vmwareなどの仮想化ソフトを使うよりずっと軽いのが嬉しいです。windowsとの分業がしやすいのも大きな利点かと。次はsshdなどサーバ系のソフトをいろいろ試してみたいと思います。
追記
上で書いたかな漢字変換サーバとlxterminalの起動を自動化するなら、例えばhome directoryの.bashrcの末尾に
if [ $SHLVL -eq 1 ]; then
if DISPLAY=localhost:0.0 xset q > /dev/null 2>&1 ; then
DISPLAY=localhost:0.0 UIM_CANDWIN_PROG=uim-candwin-gtk uim-xim &
DISPLAY=localhost:0.0 XMODIFIERS="@im=uim" GTK_IM_MODULE=uim QT_IM_MODULE=uim lxterminal &
fi
fi
のように書けばいいでしょう。最初に起動されたbashで、なおかつXが利用可能なら、かな漢字変換サーバとlxterminalを起動します。次のwindows10の大型アップデートでubuntu 16.04になるとか日本語入力も普通に出来るようになるとか噂が聞こえてくるので、そのときにはここに書いたことの大半は無意味になってしまうかもしれません。
この記事は、次のページを参考に書きました。
- Bash on Ubuntu on Windowsメモ
- Bash on Ubuntu on Windowsをインストールしてみよう!
- Bash on Ubuntu on Windows とX Windowの組み合わせで日本語表示と日本語入力
- 俺の Bash on Windows10 環境
- Bash on Ubuntu on WindowsでTensorFlowを使うためのメモ
- Cygwin絶対殺すマン ~物理のオタクがWindows Subsystem for Linuxで数値計算できるようになるまで~
2016/08/03(水)半精度浮動小数点数に関する思考実験
IEEE754-2008の半精度では、16bitを符号s(1bit)+指数部e(5bit)+仮数部m(10bit)に分割しています。指数部のオフセットは15で、従って正規化数は
x = (-1)s × 1.m × 2e-15のように、非正規化数は
x = (-1)s × 0.m × 2-14のように実数xと対応します。
ところで、URRという浮動小数点数の表現形式をご存知でしょうか。浜田穂積先生が80年代(IEEE754制定より前!)に提案された浮動小数点数の表現形式です。詳細は
- 浜田 穂積, 二重指数分割に基づくデータ長独立実数値表現法, 情報処理学会論文誌, Vol.22, No. 6, pp. 521-526 (1981)
- 浜田 穂積, 二重指数分割に基づくデータ長独立実数値表現法II, 情報処理学会論文誌, Vol.24, No. 2, pp. 149-156 (1983)
さて、半精度浮動小数点数は、bit数が少ないこともあって表現できる数値の範囲が非常に狭く、簡単にアンダーフローやオーバーフローを起こしてしまいます。正の最大数は何と65504です。正の最小数は、精度を保っている正規化数で2-14≃6.1×10-5、非正規化数まで考えても2-24≃5.96×10-8にすぎません。
そこで、URR的な考え方を用いて16bit浮動小数点数を構成したらどうなるか考えてみました。URRは-infやNaNが無いなど、現代のIEEE754に慣れた我々には使いにくいところもあるので、指数部と仮数部の区切りを可変にするという思想はそのままで、適当にフォーマットを定めます。指数部は、Eliasのデルタ符号を用いることにします。デルタ符号は1,2,3,…の自然数しか表せないので、指数部とデルタ符号で表す数値を
| デルタ符号 | 1 | 2 | 3 | 4 | 5 | … | 255 | 256 | … | 508 | 509 | 510 | 511 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 指数部 | 0 | -1 | 1 | -2 | 2 | … | 127 | -128 | … | -254 | ±0 | ±inf | NaN |
| デルタ符号の長さ | 1 | 3 | 3 | 5 | 5 | … | 14 | 15 | … | 15 | 15 | 15 | 15 |
| 提案方式の仮数部長 | IEEE754-2008の仮数部長 | |
|---|---|---|
| 2-254 | 1 | - |
| ⋮ | ⋮ | ⋮ |
| 2-128 | 1 | - |
| 2-127 | 2 | - |
| ⋮ | ⋮ | ⋮ |
| 2-24 | 6 | 1 |
| 2-23 | 6 | 2 |
| 2-22 | 6 | 3 |
| ⋮ | ⋮ | ⋮ |
| 2-16 | 6 | 9 |
| 2-15 | 7 | 10 |
| 2-14 | 7 | 11 |
| ⋮ | ⋮ | ⋮ |
| 2-8 | 7 | 11 |
| 2-7 | 8 | 11 |
| ⋮ | ⋮ | ⋮ |
| 2-4 | 8 | 11 |
| 2-3 | 11 | 11 |
| 2-2 | 11 | 11 |
| 2-1 | 13 | 11 |
| 20 | 15 | 11 |
| 21 | 13 | 11 |
| 22 | 11 | 11 |
| 23 | 11 | 11 |
| 24 | 8 | 11 |
| ⋮ | ⋮ | ⋮ |
| 27 | 8 | 11 |
| 28 | 7 | 11 |
| ⋮ | ⋮ | ⋮ |
| 214 | 7 | 11 |
| 215 | 7 | 11 |
| 216 | 6 | - |
| ⋮ | ⋮ | ⋮ |
| 2127 | 2 | - |
| 2128 | 1 | - |
| ⋮ | ⋮ | ⋮ |
| 2253 | 1 | - |
もちろんハードウェアのサポートが無くソフトウェアエミュレーションでは速度は絶望的ですが、将来このような優れたフォーマットが気軽に使えるようになればいいなと思っています。FPGAとかで作って遊んだりできないかなあ。