検索条件
全3件
(1/1ページ)
sudo apt install build-essential sudo apt install gcc-multilibが必要だと思います(後者が重要)。archiveを展開するとMakefileがあり、まずMakefileを書き換えます。どういうわけだか単にmakeするだけでいわゆるmake installに相当する作業を行い更にpathまで切ろうとするというお行儀の悪さなので、少し手を入れます。まず、Makefileの最初の方の
PREFIX=/usr/local/p-xscの部分を書き換えて、書き込んでもよい場所を絶対パスで指定します。自分は念の為ホームディレクトリの中の適当な場所を指定しました。また、Makefile中の
@echo "****************************************************"
@echo " Install System PATH in /etc/profile.local as root *"
@echo " or in ~/.bashrc as user *"
@echo "****************************************************"
cd profile; ./uidtest.sh ${PREFIX}
の部分で/etc/profile.localというシステムファイルに書き込もうとするので、ここは#でコメントアウトしておきます。2 test.dat test.outの内容で作成します。「2」は方程式の次元、test.datは方程式を記述するファイル、test.outは出力するファイル名です。次に、test.datを、
F1 = U2 F2 = 1 * (1-U1*U1) * U2 - U1 ;; 1 0 20 0 24 4 0 1 1 1e-16 1e-16の内容で作成し、
awa < test.inとすると、test.outが生成されます。この場合は、
ode read from file test.dat
out = 1
T_start = 0.000000000000000E+000
T_end = 2.000000000000000E+001
initial stepsize h = 0.000000000000000E+000
order p = 24
enclosure method : intersection of interval-vector and QR-decomposition
output : function values
t = 0.000000000000000E+000
[ 1.00000000000000E+000, 1.00000000000000E+000] 0.00E+000 0.0E+000
[ 1.00000000000000E+000, 1.00000000000000E+000] 0.00E+000 0.0E+000
h = 1.911222934722900E-001
t = 1.911222934722900E-001
[ 1.16970857077089E+000, 1.16970857077090E+000] 6.67E-016 5.7E-016
[ 7.61501247518094E-001, 7.61501247518095E-001] 3.34E-016 4.4E-016
h = 1.831474304199219E-001
(中略)
t = 1.993603903055191E+001
[ 2.00246009621560E+000, 2.00246009621563E+000] 2.18E-014 1.1E-014
[ 1.69827498867334E-001, 1.69827498867578E-001] 2.43E-013 1.5E-012
h = 6.396096944808960E-002
t = 2.000000000000000E+001
[ 2.00848791779841E+000, 2.00848791779843E+000] 8.00E-015 4.0E-015
[ 2.32898543064796E-002, 2.32898543066811E-002] 2.02E-013 8.7E-012
Number of integration steps: 134
Time: 1.64 sec
のようなファイルが生成されました(計算速度はLet's Note RZ4で)。時刻毎のx,yの値が区間で表示されていますが、真の軌道がこの区間内にあることが数学的に厳密に保証されています。区間の後の2つの数値はそれぞれ区間幅、相対区間幅を表しているようです。x,yそれぞれの上限、下限をプロットしてみましたが、このくらいの簡単な問題だと差はグラフ上では見えません。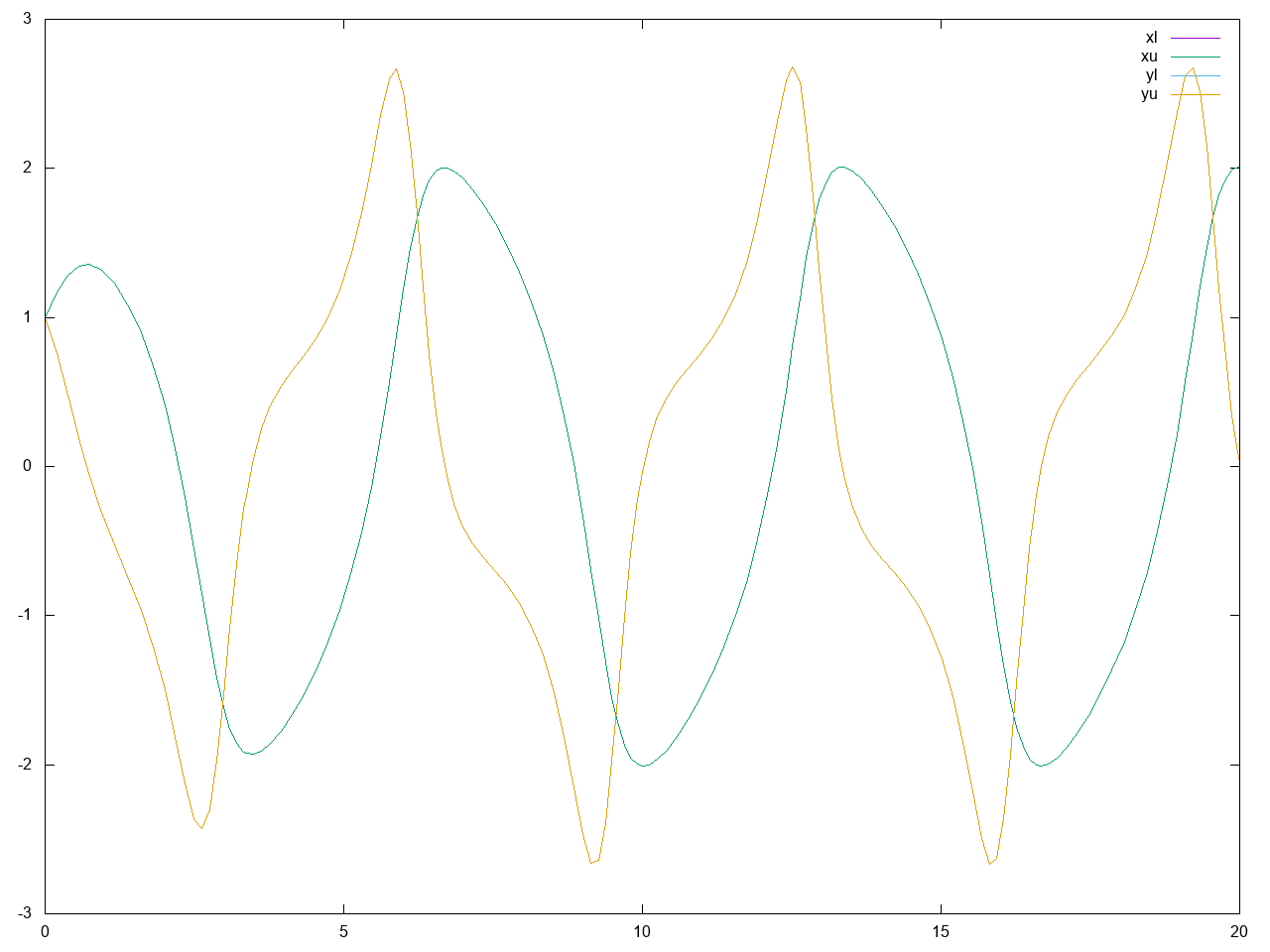
F1 = U2 F2 = 1 * (1-U1*U1) * U2 - U1 ;;方程式の右辺を記述します。変数がU1, U2で、方程式がF1, F2です。次元の数だけ記述します。
1 0 20 0 24
4 0
1 1初期値です。ここだけ少し注意が必要です。まず、初期値には、[1,2] [1,1.5]みたいな区間を書くこともできます。また、1.1のようなIEEE754のdoubleで書けないような数が与えられると、自動的にそれを包含する区間として扱います。初期値のうちどれか一つでも区間になるような場合は、
1 1.1 nのように後に「n」を補わなければなりません。「j」でもいいのですが、相対誤差の表示に影響するだけで、計算そのものには影響しません。しかし、初期値が区間になる場合はnかjのどちらかを書く必要があります。
1e-16 1e-16それぞれ、1ステップ毎に許容される絶対誤差、相対誤差を表します。