2014/12/01(月)T先生からの挑戦状続き (多倍長区間演算)
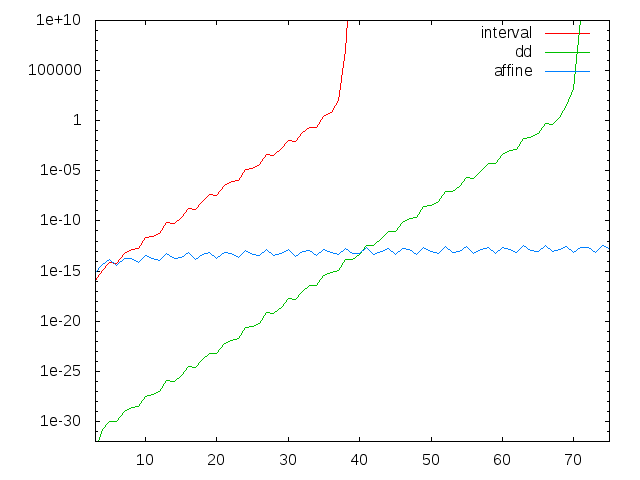
で、ddを使えば一応爆発を「遅らせる」ことは出来るので、超多倍長計算をすれば強引にn=10000まで到達させることは出来るのではないか、と推測できます。
KVライブラリはmpfrラッパーを持っており、mpfrがインストールされた環境下では簡単にmpfrを使えます。mpfrは有名な多倍長浮動小数点演算ライブラリで、最近のgccではコンパイル時に式中の定数の評価にmpfrを使ったりするので、知らないうちにインストールされていることも多いと思います。プログラムはこんな感じ。
#include <kv/interval.hpp>
#include <kv/mpfr.hpp>
#include <kv/rmpfr.hpp>
int main()
{
int i;
kv::interval< kv::mpfr<17000> > x, y, z;
std::cout.precision(17);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
コンパイル(リンク)時には-lmpfrを付けます。これを実行すると、2 [3,3] 3 [0.77777777777777777,0.77777777777777778] 4 [1.4081632653061224,1.4081632653061225] 5 [2.4744801512287334,2.4744801512287335] (中略) 9997 [1.0388807450632487,1.0388807450632488] 9998 [2.9584219778650379,2.958421977865038] 9999 [0.76071510663969069,0.7607151066396907] 10000 [1.4727965250386843,1.4727965250386844]のように、仮数部17000bitの浮動小数点数を使って、n=10000まで計算出来ました。区間幅のグラフは以下の通り。
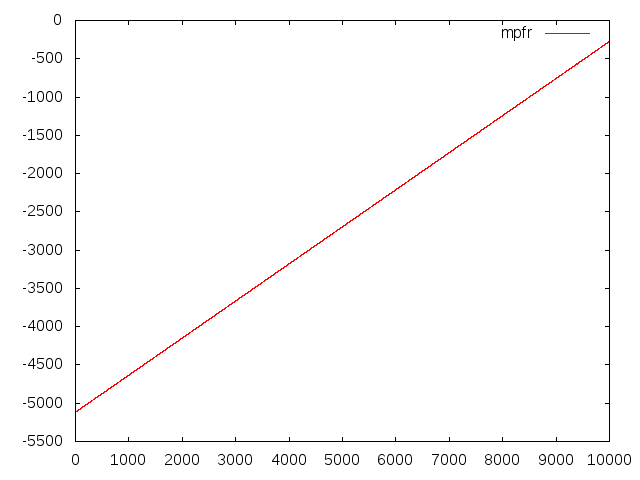
gnuplotがアンダーフローしてしまうので区間幅はlog10を取った値。有効数字10進5000桁もの計算をすれば、何とかn=10000に耐えられることが分かります。計算時間は、以下の通り。
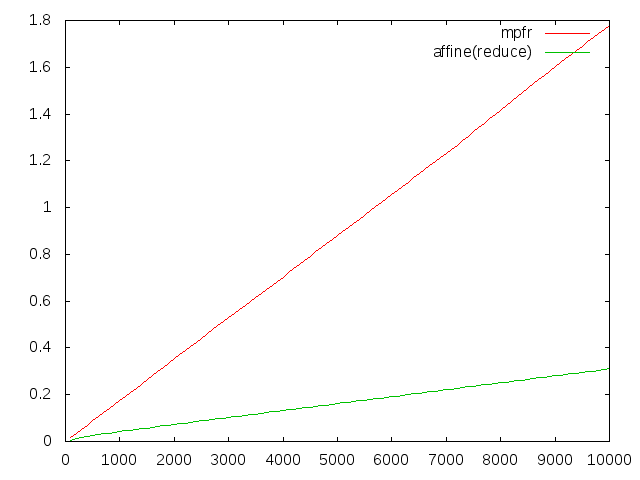
当然ながらnに対して線形。およそ2秒弱と、affine(reduce)には及ばないもののかなり高速です。しかし、例えばn=100000にしようと思うと、より仮数部のbit数が必要になり、計算時間は厳しくなるでしょう。あるいは、初期値にはじめから幅があるような計算をさせようと思うと、高精度計算しても何の意味もなく即死してしまい、affine arithmeticのような手法がどうしても必要になります。
ついでに、Y先生のところのMさんが作成した、LILIBという多倍長区間演算ライブラリを試してみました。こちらは単体で区間演算をサポートするようで、KVライブラリへの組み込みは試していません。LongFloatという多倍長浮動小数点数型に方向付き丸めの機能があれば、組み込みは可能とは思いますが。で、LILIB単体でのQRT写像計算はこちら。仮数部の長さは10進5000桁に設定しています。
#include <iostream>
#include "lilib.h"
int main(){
lilib::setPrecision(5000);
LongInterval x, y, z;
int i;
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
必要ファイルは、lilib.hとライブラリをmakeして出来るlibli.a。コンパイルは、必要ならば両者が見えるように-Iや-Lでサーチパスを設定して、-lliを付ければOK。実行結果は以下の通り。2 < 3.000000, 2.177677e-5009> 3 < 7.777778e-1, 2.177677e-5009> 4 < 1.408163, 1.328045e-5008> 5 < 2.474480, 7.583944e-5008> (中略) 9997 < 1.038881, 3.292724e-167> 9998 < 2.958422, 2.823943e-166> 9999 < 7.607151e-1, 2.314535e-166> 10000 < 1.472797, 1.307194e-165>中心半径型の表記になっていて、中心の表示に大きな丸め誤差が入っていそうなのが気になりますが、ちゃんと計算できているようです。
計算時間は260秒ほどで、残念ながらmpfrには大きく負けてしまいました。今後の発展に期待です。