2016/12/03(土)double-double演算が異常に高精度になる!?
いわゆる普通の電卓で、適当な数(例えば100)を入れて、平方根のボタンを何回か押して、次に二乗(多くの電卓で[×][=]という操作)を同じ回数だけ行います。このとき、その回数がある程度以上多いと、丸め誤差でちゃんと100に戻ってきません。100円ショップに売っていた8桁のごく普通の電卓で試してみたところ、
100 → (10回平方根) → 1.0045072 → (10回二乗) → 99.9806と、誤差が観測されました。更に回数を増やしてみると、
100 → (20回平方根) → 1.0000042 → (20回二乗) → 81.635475
100 → (25回平方根) → 1 → (25回二乗) → 1のようになりました。平方根を取った値は徐々に1に近づき、1+εのεを保持する桁数が徐々に小さくなっていって、誤差がひどくなっていく様子がよく分かります。
もちろん、普通のPCで倍精度(double)を用いても同じことで、誤差が入ります。
#include <iostream>
#include <cmath>
int main()
{
int i;
double x;
std::cout.precision(17);
x = 100;
for (i=0; i<10; i++) {
x = sqrt(x);
}
for (i=0; i<10; i++) {
x = x * x;
}
std::cout << x << "\n";
}
を実行すると、100.00000000000637のように誤差が入りました。kvライブラリを使って区間演算にしてみます。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
typedef kv::interval<double> itv;
int main()
{
int i;
itv x;
std::cout.precision(17);
x = 100;
for (i=0; i<10; i++) {
x = sqrt(x);
}
for (i=0; i<10; i++) {
x = x * x;
}
std::cout << x << "\n";
}
すると、[99.99999999997776,100.00000000004346]のように100を含む区間が得られます。
さて、ここからが本題です。このdoubleで区間演算をしたときの区間幅を、平方根と二乗の回数を変化させながらプロットしてみます。
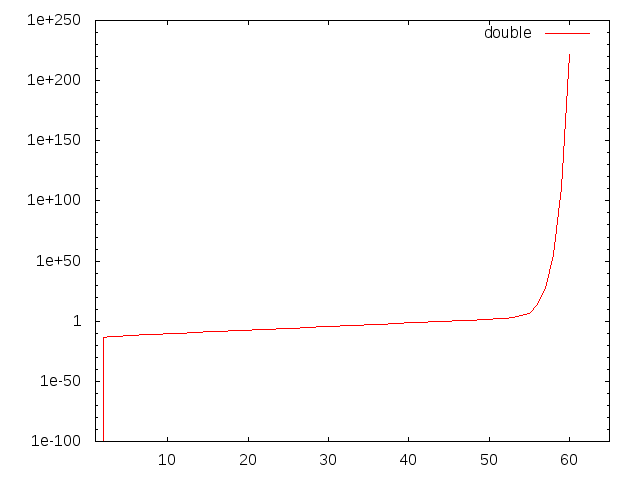
60回手前で計算が破綻していることが分かります。どこまで行けるかは仮数部の長さで決まる筈なので、mpfrを使って仮数部長を変化させて比較してみます。
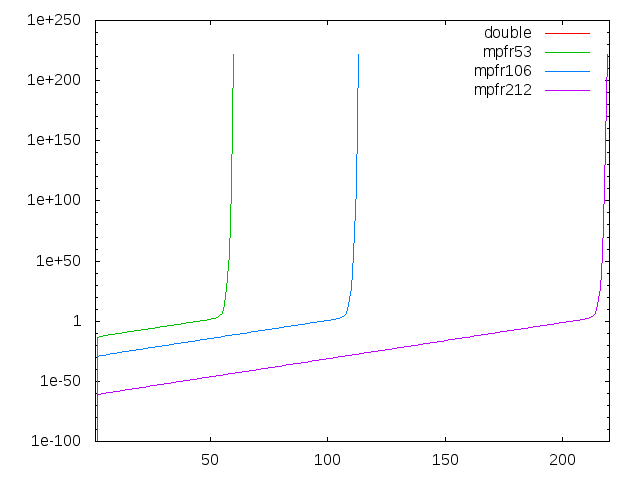
すると、mpfrの仮数部を53bit(doubleと同じ)にした場合はdoubleとぴったり同じ、mpfrの仮数部長を長くすればそれだけ破綻までの回数が大きくなっています。ここまでは予想通り。ここで、このグラフにdd(double-double演算による擬似4倍精度、仮数部は106bit相当)を追加してみましょう。
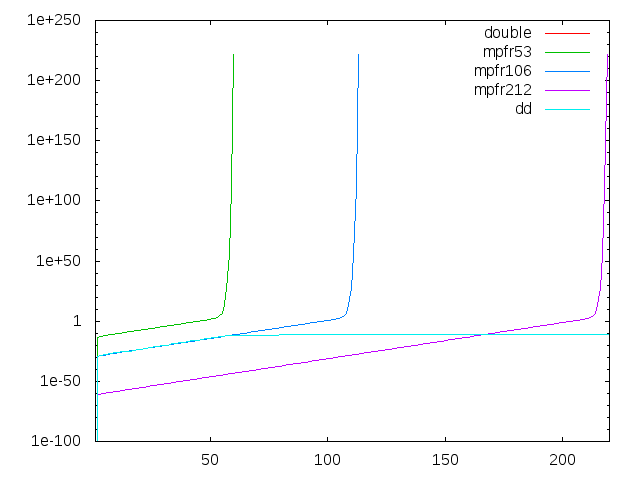
なんだか異常なグラフが得られました。仮数部106bit相当なのでmpfr106と同じ動きをすると思いきや、最初は同じ挙動を示すものの途中から全く精度の悪化が見られず、mpfr212をも凌ぐ精度を叩きだしています。そんな馬鹿なとmpfrの超高精度を追加してみます。
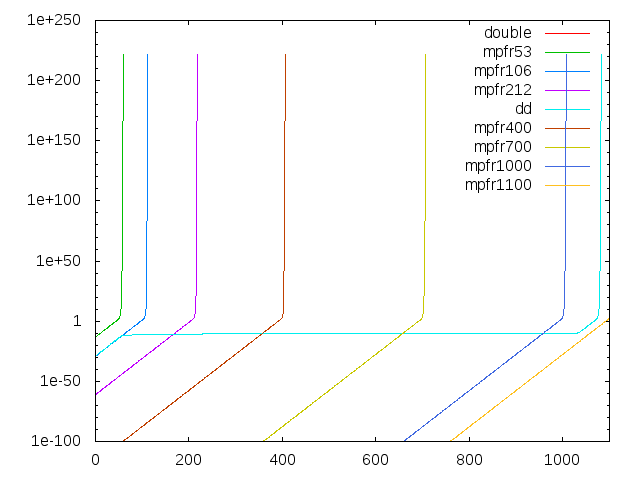
すると、mpfrの仮数部1100bitで、ようやくddに勝つことができました。この現象は、
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
typedef kv::interval< kv::dd > itv;
int main()
{
int i;
itv x;
std::cout.precision(17);
x = 100;
for (i=0; i<10; i++) {
x = sqrt(x);
}
for (i=0; i<10; i++) {
x = x * x;
}
std::cout << x << "\n";
}
のようなプログラムで区間幅を観察すれば容易に確かめられます。さて、なぜこんなことが起きたのでしょうか。最初はバグを疑ったのですが、バグではありませんでした。後日この現象の原因を追記しようと思いますので、少し考えてみて下さい。
解答 (12月4日追記)
一日経ったので理由を簡単に説明します。まず、ddとmpfr106で、平方根を40回行った場合の値を見比べてみます。表示は40桁にしました。
[1.000000000004188377884927590880100368969,1.000000000004188377884927590880168161704] (dd)ここではほぼ違いは見られません。上限と下限で一致している桁数は32桁で、4倍精度としては普通です。次に、平方根を80回にしてみます。
[1.000000000004188377884927590880118857896,1.000000000004188377884927590880168161704] (mpfr106)
[1.000000000000000000000003809307495356531,1.000000000000000000000003809307495356571] (dd)こちらは顕著な違いが見られます。mpfrの方は32桁で変わっていませんが、ddの方は38桁も一致していることが分かります。
[1.000000000000000000000003809307449647879,1.000000000000000000000003809307498951686] (mpfr106)
これは、ddの内部表現の特殊性によるものです。ddは、簡単にいうと仮数部の上位53bitと下位53bitを分割して格納するようなフォーマットです。よって、上位と下位の指数部は53ずれるのが普通なのですが(正確には下位の符号が利用できるので54ずれる)、上位と下位の間に0(上位と下位の符号が違う場合は1)が連続するような場合、それを省略することができ、上位と下位の指数部のずれが大きくなって仮数部長が大きくなることがあります。この場合も、40回のときの値の内部表現を見ると、
1.000000000004188427382700865564-4.9497773274684e-17ですが、80回のときは
1+3.8093074953565e-24で上位と下位が大きく離れています。たまたま収束先が1(=doubleで正確に表現可能)で、1+εのεの精密な表現力が問われるような問題だったので、ddが異常に高精度になったという仕掛けでした。
極めてレアな現象でいつもこういうことが起きるわけではないですが、偶然出会ったので記事に残しておきたくなったのでした。