2020/06/21(日)Ubuntu 20.04のBLAS (dgemm) をベンチマーク
BLASとは
BLAS (Basic Linear Algebra Subprograms) は、行列とベクトルの単純な操作を行うプログラム群です。有名な数値線形代数のプログラム集である LAPACK (Linear Algebra PACKage) の内部で使われています。行列とベクトルの操作は、特に最近のキャッシュメモリに依存したアーキテクチャのCPUではCPU毎に最適な書き方が異なるので、LAPACK本体から切り離して自由に差し替えられるようにしておき、ユーザがLAPACKを動かすときにその計算機に最適なBLASに差し替えることによってLAPACKは最高の性能を発揮するようにデザインされています。Ubuntu 20.04で使えるBLAS
Ubuntu 20.04で探してみたところ、aptで簡単にインストールできるBLASが5種類ありました。それぞれの特徴と、インストールコマンドを書いておきます。- Reference BLAS
sudo apt install libblas-devLAPACKと一緒に配布されているBLAS。入出力インターフェースのReferenceを与える、という意味合いと思われ、中身は単なるfor文で高速化を考慮したものではありません。
- ATLAS (Automatically Tuned Linear Algebra Software)
sudo apt install libatlas-base-devCPUの特性に合わせて自動的に各種パラメータをチューニングして性能を引き出すBLASです。make時に何通りもの大きさの計算を繰り返して最適な大きさを探るため、makeにはものすごく時間がかかります。実行するマシン上でmakeしないと意味がないので、aptによるbinary配布では本来の性能は発揮できないはずです。
sudo apt install libblis-devUbuntu 20.04で使えるBLASを探していて、今回初めて知ったBLAS実装です。最近できたものでしょうか。AOCL (AMD Optimizing CPU Libraries) で採用されていたので、AMDのCPUに強いのかも知れません。
sudo apt install libopenblas-base sudo apt install libopenblas-dev有名なオープンソース実装のBLAS。かつて、GotoBLASというテキサス大学の後藤和茂氏による高速で有名なBLAS実装があって、その後藤氏のIntelへの移籍で開発が中断したとき、有志がそのソースコードを引き継いで発展させたものです。その後藤氏は現在Intelで後述のMKLに関わっているそうです。
sudo apt install intel-mklIntelが提供している、BLASを含む数学用ソフトウェアパッケージで、オープンソースではありません。最近、aptで簡単にインストールできるようになりました。極めて高速とされています。
さて、これらは同じBLASの機能を提供するshared libraryです。同時にインストールすると上書きされてしまうのでしょうか? Ubuntuではそのような場合にsymbolic linkを利用してファイルを切り替える機能を提供しています。上記の5つのライブラリをインストールした状態で、
sudo update-alternatives --config libblas.so-x86_64-linux-gnuとすると、
There are 5 choices for the alternative libblas.so-x86_64-linux-gnu (providing /usr/lib/x86_64-linux-gnu/libblas.so). Selection Path Priority Status ------------------------------------------------------------ 0 /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so 100 auto mode 1 /usr/lib/x86_64-linux-gnu/atlas/libblas.so 35 manual mode * 2 /usr/lib/x86_64-linux-gnu/blas/libblas.so 10 manual mode 3 /usr/lib/x86_64-linux-gnu/blis-openmp/libblas.so 80 manual mode 4 /usr/lib/x86_64-linux-gnu/libmkl_rt.so 1 manual mode 5 /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so 100 manual mode Press <enter> to keep the current choice[*], or type selection number:のように表示され、「*」の印がついたライブラリが現在使われているもので、番号を入れるとそのライブラリに切り替えることができます。これはlibblas.soを切り替えるものですが、libblas.so.3も同様にupdate-alternativesの管理下にあるようで、念の為そちらも同じように切り替えて実験しました。
sudo update-alternatives --config libblas.so.3-x86_64-linux-gnu
There are 5 choices for the alternative libblas.so.3-x86_64-linux-gnu (providing /usr/lib/x86_64-linux-gnu/libblas.so.3). Selection Path Priority Status ------------------------------------------------------------ 0 /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 100 auto mode 1 /usr/lib/x86_64-linux-gnu/atlas/libblas.so.3 35 manual mode * 2 /usr/lib/x86_64-linux-gnu/blas/libblas.so.3 10 manual mode 3 /usr/lib/x86_64-linux-gnu/blis-openmp/libblas.so.3 80 manual mode 4 /usr/lib/x86_64-linux-gnu/libmkl_rt.so 1 manual mode 5 /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 100 manual mode Press <enter> to keep the current choice[*], or type selection number:
ベンチマーク
これらの5つのライブラリについて、DGEMM (倍精度行列積) の速度を計測してみました。使ったプログラムは、次のようなものです。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// prototype declaration
void dgemm_(char *transA, char *transB, int *m, int *n, int *k, double *alpha, double *A, int *ldA, double *B, int *ldB, double *beta, double *C, int *ldC);
int main(int argc, char **argv)
{
int i, j;
int m, n, k;
int size;
double *a, *b, *c;
double alpha, beta;
int lda, ldb, ldc;
struct timespec ts1, ts2;
size = atoi(argv[1]);
m = size;
n = size;
k = size;
a = (double *)malloc(sizeof(double) * m * k); // m x k matrix
b = (double *)malloc(sizeof(double) * k * n); // k x n matrix
c = (double *)malloc(sizeof(double) * m * n); // m x n matrix
for (i=0; i<m; i++) {
for (j=0; j<k; j++) {
a[i + m * j] = rand() / (1.0 + RAND_MAX);
}
}
for (i=0; i<k; i++) {
for (j=0; j<n; j++) {
b[i + k * j] = rand() / (1.0 + RAND_MAX);
}
}
for (i=0; i<m; i++) {
for (j=0; j<n; j++) {
c[i + m * j] = 0;
}
}
alpha = 1.;
beta = 0.;
lda = m;
ldb = k;
ldc = m;
// dgemm_(TransA, TransB, M, N, K, alpha, A, LDA, B, LDB, beta, C, LDC)
// C = alpha * A * B + beta * C
// A=M*K, B=K*N, N=M*N
// Trans: "N"/"T"/"C"
// LDA = number of row of A
clock_gettime(CLOCK_REALTIME, &ts1);
dgemm_("N", "N", &m, &n, &k, &alpha, a, &lda, b, &ldb, &beta, c, &ldc);
clock_gettime(CLOCK_REALTIME, &ts2);
printf("%g\n", (ts2.tv_sec - ts1.tv_sec) + (ts2.tv_nsec - ts1.tv_nsec) / 1e9);
free(a);
free(b);
free(c);
return 0;
}
BLASはFortranで書かれていて、C言語から呼びやすくしたcblasというインターフェースもあるのですが、ここでは直接BLASを呼び出しています。n×n行列を2つ乱数で初期化し、その積を求めています。また、参考のために単なるfor文のi-j-k loopで書いた行列積のプログラムとも比較してみました。そのプログラムは以下の通り。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double **alloc_matrix(int n, int m)
{
double **a;
int i;
a = (double **)malloc(sizeof(double *) * n);
a[0] = (double *)malloc(sizeof(double) * n * m);
for (i=1; i<n; i++) {
a[i] = a[0] + i * m;
}
return a;
}
void free_matrix(double **a)
{
free(a[0]);
free(a);
}
// a: n x m, b: m x s, c: n x s
void m_m_mul(double **a, double **b, double **c, int n, int m, int s)
{
int i, j, k;
int i1, j1, k1;
for (i=0; i<n; i++) {
for (j=0; j<s; j++) {
c[i][j] = 0.0;
}
}
for (i=0; i<n; i++) {
for (j=0; j<s; j++) {
for (k=0; k<m; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
}
int main(int argc, char **argv)
{
int i, j, n;
double **a;
double **b;
double **c;
struct timespec ts1, ts2;
n = atoi(argv[1]);
a = alloc_matrix(n,n);
b = alloc_matrix(n,n);
c = alloc_matrix(n,n);
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
a[i][j] = rand()/(1.0 + RAND_MAX);
b[i][j] = rand()/(1.0 + RAND_MAX);
}
}
clock_gettime(CLOCK_REALTIME, &ts1);
m_m_mul(a, b, c, n, n, n);
clock_gettime(CLOCK_REALTIME, &ts2);
printf("%g\n", (ts2.tv_sec - ts1.tv_sec) + (ts2.tv_nsec - ts1.tv_nsec) / 1e9);
free_matrix(a);
free_matrix(b);
free_matrix(c);
return 0;
}
これらを、cc -O3 dgemm.c -lblas cc -O3 forloop.cのようにコンパイルしました。
環境は、core i7 9700、Ubuntu 20.04で、dockerの中で計算しました。ただ、core i7 9700は8コアですが、どういうわけか8コアで計算させると非常に不安定で、BIOSで1コア殺して7コア生かすという特殊な環境で計算させました。
結果は、次のようになりました。
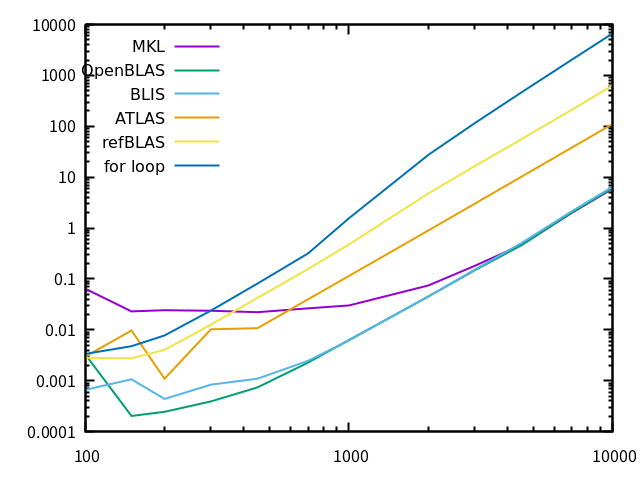
横軸は行列サイズ、縦軸は計算時間です。なお、すべて一回しか計測していないため、特に小さいサイズの行列で計算時間が短いあたりは信頼性が低いです。参考程度に見て下さい。
MKL、OpenBLASは、自動的にマルチコアを使って計算してくれました。BLISは、
OMP_NUM_THREADS=8 ./a.outのように環境変数をつけてあげるとその数のコアを使って計算しますが、何も付けないとシングルコアになりました。ATLAS、Reference BLASはシングルコア計算でした (ATLASはこのマシンでmakeすればマルチコアを使うはずです、念の為)。
マルチコアを使い、また十分チューニングされていると思われる3つは、非常に速いです。特にBLISは知らなかったのですが、十分完成度は高そうです。Reference BLASはこんなもんでしょう。自作i-j-k loopは更に非常に遅いですが、例えばi-j-kをi-k-jにするだけで結構違うはずです。
このグラフを見ると、MKLの小サイズ行列が妙に遅いのが気になります。巨大行列でガンガン計算する分には気にならないでしょうが、用途によってはこれでは困りそう。何か使い方を間違っているのかな?