2014/11/29(土)T先生からの挑戦状
問題は単純で、QRT(Quispel–Roberts–Thompson)写像と呼ばれる次のような三項間漸化式の計算です。
この問題はsigma=0,1,2で保存量を持ち厳密解が分かるのですが、そのことは置いといて、この値をどこまで精度保証付きで計算できるか、という単純なミッションを考えてみました。なお、x0=x1=1, alpha=sigma=2としました。x_{n+1} = \frac{1 + \alpha x_n}{x_{n-1}x_n^\sigma}
この問題はただの式の計算なので、区間演算を使えば簡単に精度保証付きの結果が得られます。KVライブラリを使って次のようなプログラムを作り、実行してみました。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
int main()
{
int i;
kv::interval<double> x, y, z;
std::cout.precision(17);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
すると、次のようにわずかn=40程で区間幅が爆発し、計算続行不可能になってしまいます。2 [3,3] 3 [0.77777777777777767,0.7777777777777778] 4 [1.408163265306122,1.4081632653061232] 5 [2.4744801512287302,2.4744801512287369] 6 [0.68995395922102109,0.68995395922102732] 7 [2.020393474742363,2.0203934747424169] 8 [1.7898074714307314,1.7898074714308816] 9 [0.70758786005188711,0.70758786005207142] 10 [2.6951421179631256,2.6951421179651689] 11 [1.2433015085290559,1.2433015085320609] 12 [0.83688909616776363,0.8368890961738863] 13 [3.070528249027002,3.0705282490934156] 14 [0.90504123151499416,0.90504123157760075] 15 [1.1172985551574801,1.1172985553860118] 16 [2.862947305672872,2.8629473074466386] 17 [0.73443626104422132,0.73443626249187089] 18 [1.5987372263097938,1.5987372354777325] 19 [2.2360410366985798,2.2360410765188719] 20 [0.68456699674402565,0.68456703501491612] 21 [2.2608819297780762,2.2608822958754975] 22 [1.5779961588661814,1.577996967369254] 23 [0.73821770109333384,0.73821886432301598] 24 [2.8797219842307102,2.8797352403432291] 25 [1.1041312743805045,1.1041475101638208] 26 [0.91382523264135828,0.91386556371680073] 27 [3.0664366812454475,3.0668399350082205] 28 [0.82985073203052506,0.83019950035095925] 29 [1.2582787064685059,1.2598325118993606] 30 [2.6687606228279703,2.6788454371225426] 31 [0.70098916182277204,0.70941982097935608] 32 [1.7816188152293368,1.8444838202503787] 33 [1.890688867011997,2.1073484458445711] 34 [0.58372124794988644,0.81879304568504608] 35 [1.5341327531940911,4.0942614522583929] 36 [0.29640395761996329,6.6882779916662063] 37 [0.0086967943592607538,106.66548725824453] 38 [1.3369859317919986e-05,9560542.5436595381] 39 [1.0257053348148149e-16,1.229984619387229e+19] 40 [6.9138205018986439e-46,1.7488703313159241e+56] 41 [2.6581843623384974e-132,7.1339291414655989e+162] 42 [0,inf]徐々に区間幅が広がっていき、最後は無限大になってしまうのがよく分かります。
上記プログラムは普通の倍精度浮動小数点数(double)を両端に持つ区間を使っていましたが、KVライブラリではC++のtemplate機能を活かして内部に使う型を簡単に変更できる設計になっています。こんなときのとっておき、dd型 (double-double型、2つの倍精度浮動小数点数を使って擬似的に4倍精度計算を実現する) を使ってみます。プログラムはほんのちょっと変えるだけです。
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>
int main()
{
int i;
kv::interval<kv::dd> x, y, z;
std::cout.precision(34);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
ところが、ddを使ってもn=70程度まで延命出来ただけで、結局簡単に爆発してしまいました。2 [3,3] 3 [0.7777777777777777777777777777777769,0.7777777777777777777777777777777785] 4 [1.408163265306122448979591836734609,1.408163265306122448979591836734758] 5 [2.474480151228733459357277882797321,2.47448015122873345935727788279821] (中略) 68 [0.6606453155656627160559713888162068,2.488777554122974836656209780178813] 69 [0.3630241653215510628974534771389999,20.84686788353973331753745146411988] 70 [0.001595824920191238478402654408600081,490.3709416664303537425877558970553] 71 [2.001214498916669183276366192993567e-07,1061918772.964718820683022033686357] 72 [1.808393136079450840308481921793132e-21,33231410120507675853548034.3953333] 73 [8.527292515465346753995834778204495e-61,1.015545591623593896027227621864483e+74] 74 [2.917778899018625327831549372023697e-174,1.544593663653553016423539427761607e+215]この原因は、ちょっと分かりにくいのですが、区間演算が単に幅だけを保持して中間変数間の依存性情報を持たないことに起因します。そのせいで、わずかに混入した丸め誤差が異常に大きく成長してしまいます。精度が足りないとかそういう問題では無いのです。
そこで、単純な区間演算でなく、もう少し高度なaffine arithmeticを使用してみましょう。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
#include <kv/affine.hpp>
int main()
{
int i;
kv::affine<double> x, y, z;
std::cout.precision(17);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << to_interval(z) << "\n";
x = y;
y = z;
}
}
n=10000まで計算してもまだ10桁程度の有効数字を保っています!2 [3,3] 3 [0.77777777777777756,0.77777777777777824] 4 [1.4081632653061197,1.4081632653061247] 5 [2.4744801512287271,2.4744801512287414] (中略) 9996 [0.96392545060016987,0.96392545075868175] 9997 [1.0388807449801562,1.038880745148527] 9998 [2.9584219777870881,2.9584219779411463] 9999 [0.76071510659932817,0.76071510667899534] 10000 [1.4727965248961243,1.4727965251850226]区間幅をグラフにしてみます。
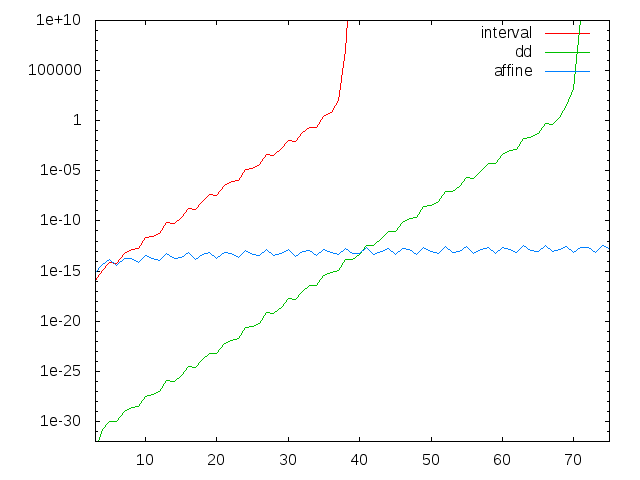
intervalとddではスタート時の誤差こそ違うものの同じような傾きで誤差が増大してしまい、死ぬのは時間の問題だということがよく分かります。n=10000まで見ると、
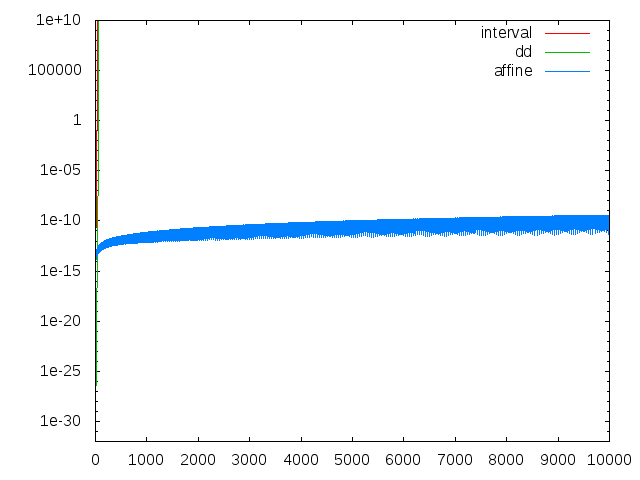
intervalとddは即死ですが、affineの安定度が光ります。
さて、affine arithmeticは、「affine arithmeticについて」に書いたように、ダミー変数の線形結合で数を表現しますが、ダミー変数の数は非線形演算を経る毎に増えていき、計算時間がかかるようになります。この例題だと、一回の反復に乗算2つと除算1つを含むのでダミー変数が3つ増え、n=10000のときには一つの数を表現するのに30000個もの変数を使うことになります。affine arithmeticでn=10000まで計算した時の計算時間をグラフにしてみます。
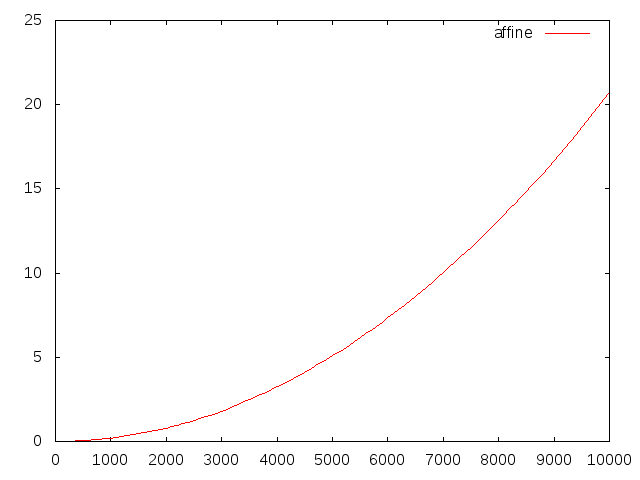
本来線形になるはずのところがダミー変数の増大のために徐々に傾きが増していき、n=10000に到達するのに20秒ほど要していることが分かります。
この写像の状態変数は2次元であり、intervalでは状態を2次元平面内の長方形で表現していることになるのに対して、affineではダミー変数の数×2の辺を持つ多角形で表現していると考えることが出来ます。しかし、たかが2次元の領域を表現するのに、60000角形を使うのはオーバースペックではないかと考えられます。
自分は、affine arithmericの表現能力をなるべく落とさずにダミー変数の数を減らすアルゴリズムを提案しています。日本語のものは無いのですが、An algorithm to reduce the number of dummy variables in affine arithmeticにロシアで発表したときのスライドがあります。このアルゴリズムはすでにKVライブラリに組み込んであって、それを使ってみます。I/Fがaffine変数のベクトルに作用するように作ってあるので、いったんベクトルにコピーしています。ダミー変数の数の上限を300に設定してみます。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
#include <kv/affine.hpp>
namespace ub = boost::numeric::ublas;
int main()
{
int i;
kv::affine<double> x, y, z;
ub::vector< kv::affine<double> > tmp(2);
std::cout.precision(17);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << ": " << to_interval(z) << "\n";
x = y;
y = z;
tmp(0) = x;
tmp(1) = y;
epsilon_reduce(tmp, 250, 300);
x = tmp(0);
y = tmp(1);
}
}
これを使うと、次のグラフのように劇的に計算時間を改善できます。
計算時間はわずか0.3秒ほどに。削減アルゴリズムを使った方のグラフを拡大すると、
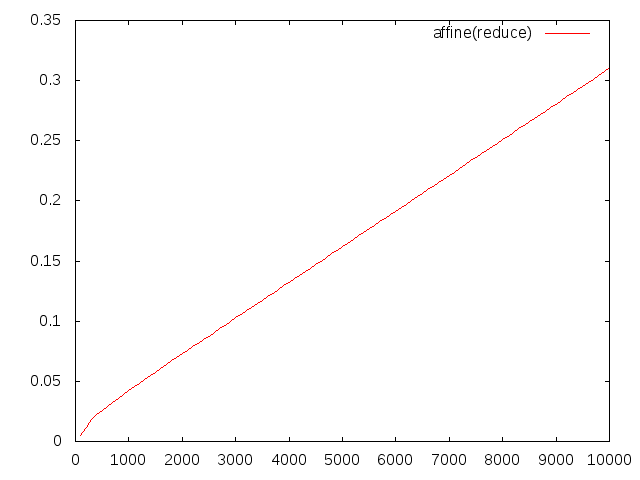
のようになり、ダミー変数の数の上限が設定されたことにより計算時間が線形になっているのが確認できます。区間幅を見ても、
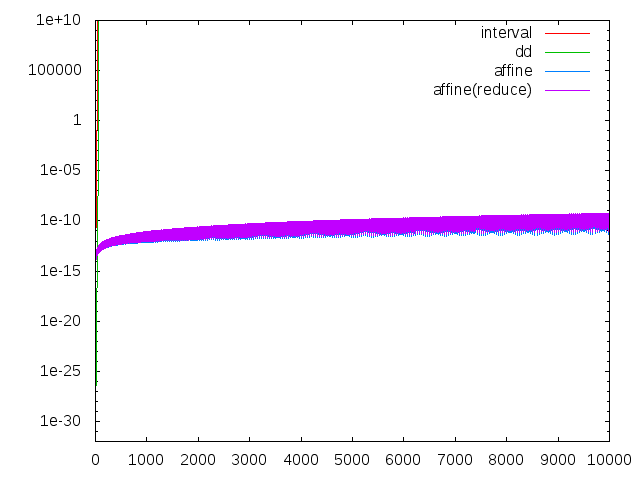
のようにほとんど増大しておらず、affine arithmeticの性能を保ったまま計算時間の削減に成功しています。
以上、区間演算とaffine arithmeticの特徴が非常によく表れた例題だったので、少し詳しく記録を残してみました。