2016/03/25(金)kv-0.4.30とstiffなODE
y=(y1,y2,y3)として、
y1' = -0.04y1 + 104y2y3
y2' = 0.04y1 - 104y2y3 - 3*107y22
y3' = 3*107y22
y1(0)=1, y2(0)=0, y3(0)=0
というものです。Robertson's Problemとして有名なもののようです。係数に非常に大きな数が見えるので、確かにヤバそうです。これをkvのODE solver(ode_maffine)で解かせてみると、確かにステップ幅が非常に小さくなってしまい、全く先に進みません。次数を変えたりいろいろ試してみても、どうにもうまく行きません。stiffな奴は本気で取り組まないといけないなあと考えていたのですが、ふと思いついて以前からkvに含まれていたode_maffine2というsolverで解かせて見ると、なんと楽に解けることが判明しました。ode_maffineに比べると1000倍くらい刻み幅が大きく取れるので、結果として同じ時刻まで計算するのに1000倍くらい速いということになります。
ODE solverは、いわゆるwrappring effectを防ぐために、解軌道の初期値に関する微分を利用しています。ode_maffineは、それを得るのに与えられた微分方程式の初期値に関する変分方程式を同時に精度保証付きで解いています。ode_maffine2はそこを少し手抜きして、推進写像を低次の部分と高次の部分に分け、定次の部分の初期値に関する微分を自動微分で計算し、高次の部分は微分を計算せず直接区間評価する、という手法で計算しています。この手法はLohnerも使っているもので、新しいものではありません。普通のODEで試すとode_maffineとode_maffine2は計算時間に大差はなく、またode_maffine2は推進写像の正確なヤコビ行列を計算しないのでshooting methodに使いづらいこともあり、ode_maffineの方を主に使っていました。
stiffなODEでこのような大きな差が出た理由を推測してみます。n2の大きさの変分方程式を精度保証する必要のあるode_maffineと、nの大きさの与えられた方程式を精度保証しさえすればよいode_maffine2では、元々精度保証可能な刻み幅の限界に大きな差があった。通常のstiffでないODEでは1ステップ毎に混入する誤差をmachine epsilon以下にするための刻み幅の限界の方が精度保証限界より小さいのでそちらに制限されてしまい、差が見えない。しかし、stiffなODEになると、精度保証可能な刻み幅の限界値が小さくなり、その差が顕著に見えるようになった、と推測できます。
問題の方程式をode_maffineとode_maffine2で解かせて見ると、t=0.00390625 (1/256)までの解を精度保証するのに、ode_maffineだとおよそ3分12秒かかったのに対して、ode_maffine2だとわずか0.02秒で終了しました。そこまでのtの分割数は前者が10842なのに対して後者はわずか6でした。また、ode_maffine2だと、t=40までの精度保証をさせても、およそ3分40秒、分割数13281でした。そのときの解は、およそ次の図のような感じでした。
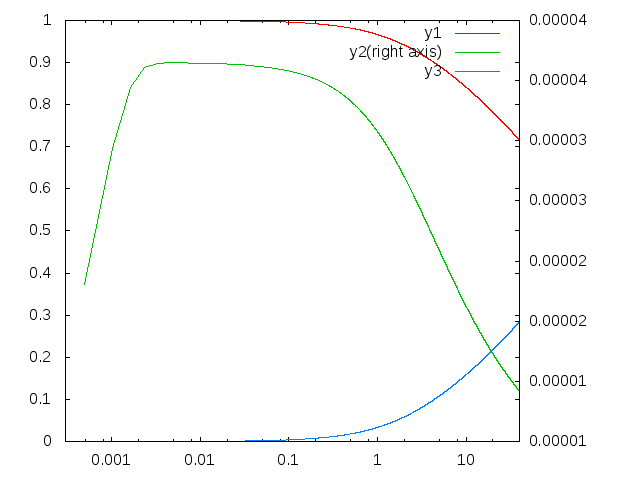
t=0からの出発直後に大きな変化があるので、あえてtを対数で表示しています。
また、このことに関連して、kvライブラリをkv-0.4.30にアップデートしました。本質的にはほとんど変わっていませんが、刻み幅の制御方法を少し変えたのと、ODEのweb demoでode_maffineとode_maffine2を選べるようにしました。example/rober.ccに今回の例題も入れておきました。