検索条件

から
検索タグ 精度保証
指定期間 2016年12月の記事
全4件 (1/1ページ)

2016/12/30(金)kv-0.4.39

精度保証
kvライブラリを0.4.39にアップデートしました。

今回は特にバグフィックスは無く、主に使い勝手に関する機能追加です
  • 大域最適化用のoptimize.hppにminimize/minimize_value/maximize/maximize_valueを追加。1変数用の関数も追加。
  • dka.hppのdka関数の収束条件を見直し。
  • 高階微分用のhighderiv.hppに、 高階微分の関数オブジェクトを生成するHighDerivと、 偏高階微分の関数オブジェクトを生成するPartialDerivを追加した。
  • allsol.hppに1変数関数用のallsol関数を追加した。
大域最適化はあまり説明もなくひっそりと実装してあったのですが、本格的に利用したくなる場面があって、それには少し使いづらいので、いろいろと関数を追加しました。説明は、「大域最適化」に詳しく書きました。

dka関数の修正は、ルジャンドル多項式のゼロ点を求めようとすると収束条件が厳しすぎてループから出てこない問題点が見つかったのがきっかけです。高次のルジャンドル多項式は係数が非常に大きく、そのため残差に入る丸め誤差が大きくなるので収束しづらくなっていたようなので、係数の大きさを見て収束条件を加減するように変更してみました。

HighDerivおよびPartialDerivは、高階(偏)微分の関数オブジェクトを生成するもので、数値積分の誤差評価に出てくる高階微分の区間評価において、optimizeと組み合わせて過大評価を抑えることを意図して作ったものです。

いずれも誰かが使っているのを見て必要性を感じて作ったもので、ユーザのありがたさを感じています。皆様、もっともっと使って下さい！
コメント（0件）

2016/12/28(水)中点はどうやって計算するべきか

精度保証
今回は非常に単純な話で、IEEE754のdoubleで表現された数a,bが与えられたとき、その中点(a+b)/2はどう計算するのが最善でしょうか、という問題です。もちろん誤差は入りますが、出来ればnearestにしたい、すなわち、真の(a+b)/2をIEEE754のルールで丸めたものを計算することを目標にします。IEEE754の内部表現は2進数ですから、2で割る操作は指数部を1減らすだけなので普通は誤差は入りません。しかし、極端な場合を考えると案外難しいのです。

(a+b)*0.5

まずは普通に足して2で割る方法。「2で割る」は「0.5を掛ける」にした方がコンパイラに優しいでしょう。ごく普通の方法で安定度抜群ですが、例えば
a=21023
b=21023
の場合、a+bがオーバーフローしてしまう問題があります。

a*0.5+b*0.5

オーバーフローを避けて先に2で割る方法です。計算量は少し増えてしまいますが。こちらは、アンダーフロー領域で問題になります。例えば、
a=2-1074
b=2-1074
のとき、a*0.5、b*0.5はともにアンダーフローで0になってしまい、結果も0になってしまいます。

a+(b-a)*0.5

これもよく見る式です。IEEE754では関係ありませんが、内部演算が10進数の場合にこうやって計算することが推奨されているのを見かけたことがあります。しかし、
a=21023
b=-21023
でオーバーフローしてしまいます。

a+b*0.5-a*0.5

上の式でオーバーフローを避けたものです。今度こそ良さそうですが、
a=5*2-1074
b=7*2-1074
としてみましょう。このとき、IEEE754の偶数丸めルールの関係で、
a*0.5=2*2-1074
b*0.5=4*2-1074
となります。よって計算結果は7*2-1074となってしまい、真の6*2-1074になりません。

a+b*0.5-a*0.5 (ただし上向き丸めで計算)

INTLAB version 9で採用している計算方法です。a*0.5とb*0.5に入る丸めの方向が逆向きになることが無いので、先の例だとうまく計算できます。しかし残念ながら必ずnearestにはならないようで、Mさんがちゃんと計算できない例を発見しました。
a=(253-1)*2-1073
b=7*2-1074
とすると、
(nearest)=2-1021+2-1073
(計算値)=2-1021+2-1072
と値がずれてしまいます。a*0.5は無誤差ですが、b*0.5と加算で両方上向き丸めになった結果、真値(2-1021+2-1073+2-1075)を丸めたものとずれてしまいました。

結論?

kvライブラリの区間の中点を計算するmid関数では、aとbの絶対値が両方共1より大きいときはa*0.5+b*0.5で、それ以外のときは(a+b)*0.5で計算しています。このようにifで場合分けをしていいなら話は簡単なのですが、matlabの場合はベクトル単位で一括処理しないとパフォーマンスが出ないのでなるべくifを使いたくないという事情があります。if文禁止で完璧な中点の計算アルゴリズムはまだ見つかっていません。誰か考えて！
コメント（0件）

2016/12/10(土)kv-0.4.38

精度保証
kvライブラリを0.4.38に更新しました。

今回は、区間演算にmidrad、max、minを追加しました。また、dka.hppの中にあるvdka (精度保証付きDKA法) で、解が重複する場合の処理をきちんと行なうようにしました。

midradとmax/minの追加は、どちらも同僚のS先生の要請によるものです。少し詳しく説明します。

midrad

midradは、区間 I に対して、
midrad(I, m, r);
とすると中心の近似mと、半径rを同時に計算します。これは、中心m、半径rの区間で I を包含する、すなわち、上端下端型の区間から中心半径型の区間への変換に使われることを意図しています。単純に
m = mid(I);
r = rad(I);
とすれば良さそうなものですが、中心mに丸め誤差が入るので、これだと I を包含しない可能性があるのです。例えば、ε=2-52として、I=[1,1+3ε]とします。このとき、midとradを別々に計算すると、
m = 1+2ε
r = 1.5ε
となりますが、[m-r,m+r]は I を含まないことが分かります。midradを使うと、ちゃんと
m = 1+2ε
r = 2ε
になります。ミスが起こりやすいポイントなので気をつけて下さい。

max, min

max, minは区間同士のmax, minです。max(I1, I2)は、x1∈I1、x2∈I2としたときのmax(x1,x2)の取り得る範囲の区間を返します。minも同様です。計算は、
max([a,b],[c,d]) = [max(a,c),max(b,d)]
min([a,b],[c,d]) = min(a,c),max(b.d)]
のように行います。

この関数は、後述するようにVisual C++と少し相性が悪いこともあって実装していなかったのですが、実装しないと思わぬバグに遭遇する可能性があると同僚のS先生に指摘され、実装することにしました。例えば、max, minを実装していないversionのkvで、
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>

typedef kv::interval<double> itv;

using namespace std;

int main()
{
    cout << max(itv(2., 4.), itv(3., 5.)) << endl;
    cout << min(itv(3., 5.), itv(2., 4.)) << endl;
}
のようなプログラムを動かすと、予想に反して
[2,4]
[3,5]
という結果が帰って来ます。これは、std::max, std::minが呼び出されてしまっており、恐らくmaxは
template <class T> 
T max(const T& a, const T& b)
{
    return (a < b) ? b : a;
}
のような実装になっていて、[2,4]<[3,5]は偽なので[2,4]が返されてしまっていると推測されます。よく考えれば分かるとは言え、これは事故を誘発しやすいので、ちゃんと区間用のmaxとminを実装しました。kv-0.4.38で上のプログラムを動かすと、ちゃんと
[3,5]
[2,4]
となります。

なお、Visual C++はwindows.hというヘッダファイルを持っており、これをincludeするとマクロでmaxとminを定義してしまうという大変極悪な仕様になっています。これがincludeされていると、max,minを定義している箇所がマクロ置換されてしまいinterval.hppがコンパイル出来ません。windows.hとkvをどうしても同時に使いたければ、
#define NOMINMAX
#include <windows.h>
のようにwindows.hをincludeする前にNOMINMAXを定義して下さい。
コメント（0件）

2016/12/03(土)double-double演算が異常に高精度になる!?

精度保証
いわゆるdouble-doubleによる4倍精度演算が不思議な挙動を示した例を見つけたので、メモしておきます。

いわゆる普通の電卓で、適当な数(例えば100)を入れて、平方根のボタンを何回か押して、次に二乗(多くの電卓で[×][=]という操作)を同じ回数だけ行います。このとき、その回数がある程度以上多いと、丸め誤差でちゃんと100に戻ってきません。100円ショップに売っていた8桁のごく普通の電卓で試してみたところ、
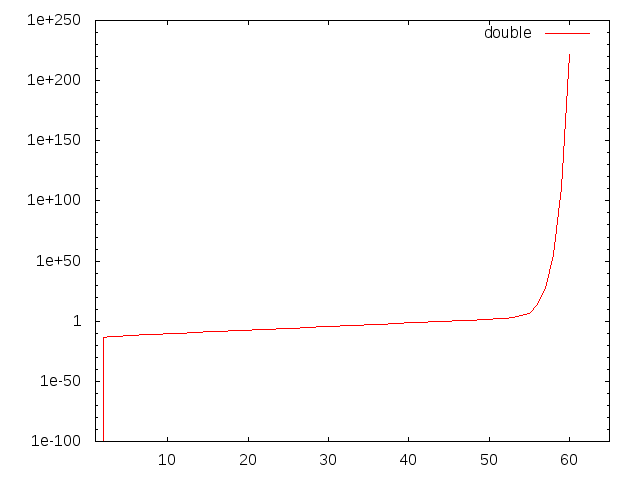
100 → (10回平方根) → 1.0045072 → (10回二乗) → 99.9806
と、誤差が観測されました。更に回数を増やしてみると、
100 → (20回平方根) → 1.0000042 → (20回二乗) → 81.635475
100 → (25回平方根) → 1 → (25回二乗) → 1
のようになりました。平方根を取った値は徐々に1に近づき、1+εのεを保持する桁数が徐々に小さくなっていって、誤差がひどくなっていく様子がよく分かります。

もちろん、普通のPCで倍精度(double)を用いても同じことで、誤差が入ります。
#include <iostream>
#include <cmath>

int main()
{
	int i;
	double x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}
を実行すると、
100.00000000000637
のように誤差が入りました。kvライブラリを使って区間演算にしてみます。
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>

typedef kv::interval<double> itv;

int main()
{
	int i;
	itv x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}
すると、
[99.99999999997776,100.00000000004346]
のように100を含む区間が得られます。

さて、ここからが本題です。このdoubleで区間演算をしたときの区間幅を、平方根と二乗の回数を変化させながらプロットしてみます。
sqrt1.png

60回手前で計算が破綻していることが分かります。どこまで行けるかは仮数部の長さで決まる筈なので、mpfrを使って仮数部長を変化させて比較してみます。
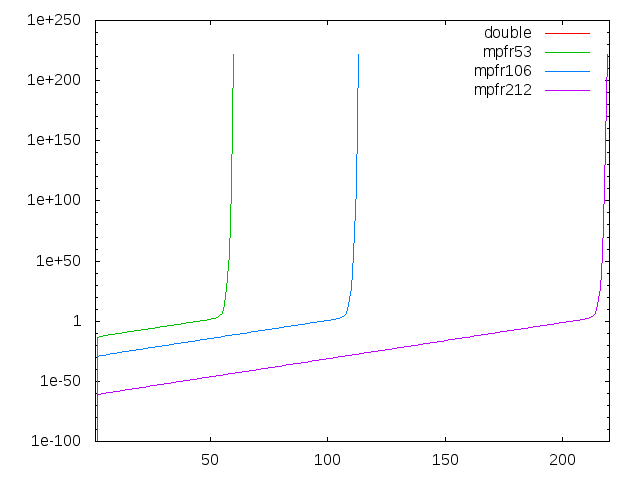
sqrt2.png

すると、mpfrの仮数部を53bit(doubleと同じ)にした場合はdoubleとぴったり同じ、mpfrの仮数部長を長くすればそれだけ破綻までの回数が大きくなっています。ここまでは予想通り。ここで、このグラフにdd(double-double演算による擬似4倍精度、仮数部は106bit相当)を追加してみましょう。
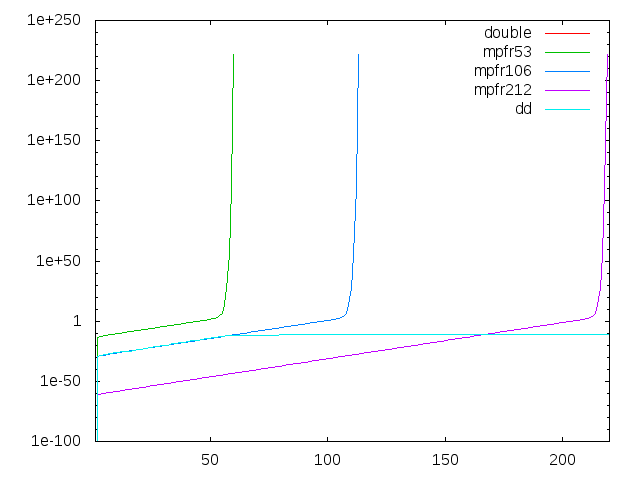
sqrt3.png

なんだか異常なグラフが得られました。仮数部106bit相当なのでmpfr106と同じ動きをすると思いきや、最初は同じ挙動を示すものの途中から全く精度の悪化が見られず、mpfr212をも凌ぐ精度を叩きだしています。そんな馬鹿なとmpfrの超高精度を追加してみます。
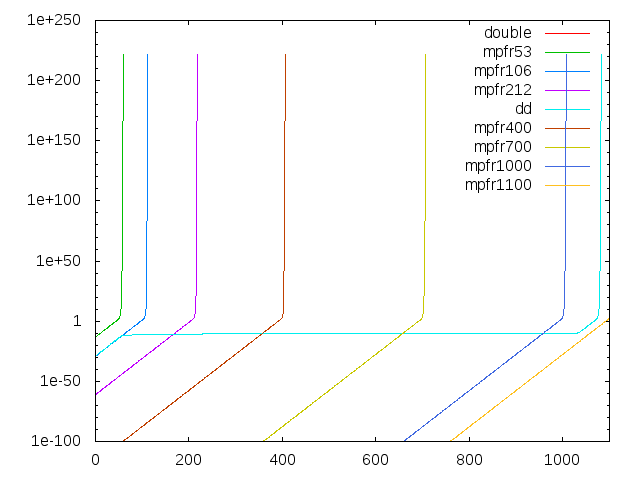
sqrt4.png

すると、mpfrの仮数部1100bitで、ようやくddに勝つことができました。この現象は、
#include <kv/interval.hpp>
#include <kv/dd.hpp>
#include <kv/rdd.hpp>

typedef kv::interval< kv::dd > itv;

int main()
{
	int i;
	itv x;

	std::cout.precision(17);

	x = 100;
	
	for (i=0; i<10; i++) {
		x = sqrt(x);
	}

	for (i=0; i<10; i++) {
		x = x * x;
	}

	std::cout << x << "\n";
}
のようなプログラムで区間幅を観察すれば容易に確かめられます。

さて、なぜこんなことが起きたのでしょうか。最初はバグを疑ったのですが、バグではありませんでした。後日この現象の原因を追記しようと思いますので、少し考えてみて下さい。

解答 (12月4日追記)

一日経ったので理由を簡単に説明します。

まず、ddとmpfr106で、平方根を40回行った場合の値を見比べてみます。表示は40桁にしました。
[1.000000000004188377884927590880100368969,1.000000000004188377884927590880168161704] (dd)
[1.000000000004188377884927590880118857896,1.000000000004188377884927590880168161704] (mpfr106)
ここではほぼ違いは見られません。上限と下限で一致している桁数は32桁で、4倍精度としては普通です。次に、平方根を80回にしてみます。
[1.000000000000000000000003809307495356531,1.000000000000000000000003809307495356571] (dd)
[1.000000000000000000000003809307449647879,1.000000000000000000000003809307498951686] (mpfr106)
こちらは顕著な違いが見られます。mpfrの方は32桁で変わっていませんが、ddの方は38桁も一致していることが分かります。

これは、ddの内部表現の特殊性によるものです。ddは、簡単にいうと仮数部の上位53bitと下位53bitを分割して格納するようなフォーマットです。よって、上位と下位の指数部は53ずれるのが普通なのですが(正確には下位の符号が利用できるので54ずれる)、上位と下位の間に0(上位と下位の符号が違う場合は1)が連続するような場合、それを省略することができ、上位と下位の指数部のずれが大きくなって仮数部長が大きくなることがあります。この場合も、40回のときの値の内部表現を見ると、
1.000000000004188427382700865564-4.9497773274684e-17
ですが、80回のときは
1+3.8093074953565e-24
で上位と下位が大きく離れています。たまたま収束先が1(=doubleで正確に表現可能)で、1+εのεの精密な表現力が問われるような問題だったので、ddが異常に高精度になったという仕掛けでした。

極めてレアな現象でいつもこういうことが起きるわけではないですが、偶然出会ったので記事に残しておきたくなったのでした。
コメント（0件）
OK キャンセル 確認 その他