検索条件
全2件
(1/1ページ)
2018/12/26(水)三部会連携 応用数理セミナー
そこでつかったスライドを上げておきます。
40分では少し駆け足になってしまったのが反省点。また、Affine Arithmeticは常微分方程式の精度保証でかなり重要な役割を果たしているにもかかわらず、教科書のどこにも説明がないのが大きな問題点だなあと感じました。
2018/12/09(日)Intlab 11の精度保証付きODE Solver
一つは、先ごろ紹介したLohnerのAWAを移植したAWA Toolboxです。AWAはPascal-XSCというマイナーな言語で書かれていますから、メジャーなMATLABで書かれていた方がありがたい、という人もいるでしょう。
もう一つは、Berz, Makinoによる精度保証付き初期値問題ソルバーCOSY INFINITYを移植した Taylor model toolbox です。解を初期値に関して高次に展開することによる非常に高性能な精度保証付きアルゴリズムとして知られています。
今回は、この両者を実際に動かしてみたレポートです。MATLABはLinux上でR2018aを使いました。
まずはIntlab 11を買います。PayPalで支払うと、メールで6時間有効なダウンロードリンクが送られてくるので、INTLAB.zipをダウンロードしておきましょう。中身のファイルそのものは特にプロテクトがかかっているわけではなく自由に使えます。Intlabのインストールは簡単で、zipを解凍して好きなディレクトリに置くだけです。Intlabの機能を使う前に、MATLABでそのディレクトリにcdして startintlab とタイプします。初回はいろいろ調査するため時間がかかります。注意点は、IntlabはMATLABとoctave(MATLAB互換フリーソフト)に対応していますが、残念ながら精度保証付き初期値問題のためのAWA toolboxとTaylor model toolboxはoctaveに対応していません。octaveでのテストを行わずに開発していたそうで、またいくつかのoctaveの非互換の部分が問題ですぐに対応するのは難しいそうです。
次に実際に動かしてみます。例題は、以前LohnerのAWAを紹介した記事と同じ、van der Pol方程式:
\begin{align*}
\frac{dx}{dt} &= y \\
\frac{dy}{dt} &= \mu (1-x^2)y - x
\end{align*}
で、\mu=1とし、初期値 (x(0),y(0))=(1,1)でt\in[0,20]の範囲で計算する問題にしました。AWA toolbox
まずAWA toolboxの方の使い方を説明します。詳細はDEMOAWA Short demonstration of the AWA toolboxのページを見て下さい。最小限のコードはこんな感じだと思います。これを適当な名前 (例えばhoge.m) でファイルを作成し、MATLAB上でhogeで実行できます。
init = [1; 1];
[T,X] = awa(@vdp, @vdp_J, [0, 20], init);
format long e
awa_disp(T,X);
function f = vdp(t, x)
mu = 1;
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
end
function J = vdp_J(t, x)
mu = 1;
J = [typeadjust(0, x), typeadjust(1, x);
-2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end
このように、ODEの右辺を定義する関数(ここではvdp)と、そのヤコビ行列を返す関数(ここではvdp_J)を定義し、関数awaを呼びます。awaの計算したデータを分かりやすく表示してくれるのがawa_dispです。ヤコビ行列を定義するのが面倒ですし、Intlabの持っている自動微分機能でなんとかなりそうな気がするのですが、高速化のためにやむを得なかったそうです。typeadjustという関数が使われていますが、関数の戻り値に定数があるときはこうやって型を補正する必要があります。更に、関数awaの第5引数に
awaset('order',10,'h0',0,'EvalMeth',4,'AbsTol',1e-16,'RelTol',1e-16)
のような関数を使って、様々なパラメータを変更することができます(これらの値はデフォルト値)。変更したいパラメータの名前を奇数番目の引数に、値を偶数番目の引数に書きます。これを使って、LohnerのAWAを紹介した記事に合わせてTaylor展開の次数を24次にした、
init = [1; 1];
tic; [T,X] = awa(@vdp, @vdp_J, [0, 20], init, awaset('order', 24)); toc
format long e
awa_disp(T,X);
function f = vdp(t, x)
mu = 1;
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
end
function J = vdp_J(t, x)
mu = 1;
J = [typeadjust(0, x), typeadjust(1, x);
-2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end
を実行してみました。すると、次のような解が得られました。
経過時間は 20.973900 秒です。
t = 0
[y_1] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_1]) = 0.00e+00
[y_2] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_2]) = 0.00e+00
t = 1.911224186649680e-01
[y_1] = [ 1.169708666105268e+000, 1.169708666105269e+000] d([y_1]) = 6.66e-16
[y_2] = [ 7.615010659752849e-001, 7.615010659752856e-001] d([y_2]) = 4.44e-16
(中略)
t = 1.992657858092985e+01
[y_1] = [ 2.000739935214436e+000, 2.000739935214461e+000] d([y_1]) = 2.31e-14
[y_2] = [ 1.939352117515359e-001, 1.939352117517785e-001] d([y_2]) = 2.42e-13
t = 20
[y_1] = [ 2.008487917798417e+000, 2.008487917798427e+000] d([y_1]) = 7.99e-15
[y_2] = [ 2.328985430648321e-002, 2.328985430667890e-002] d([y_2]) = 1.96e-13
オリジナルのAWAのt=20における解は、t = 2.000000000000000E+001 [ 2.00848791779841E+000, 2.00848791779843E+000] 8.00E-015 4.0E-015 [ 2.32898543064796E-002, 2.32898543066811E-002] 2.02E-013 8.7E-012でした。どちらも精度保証付きソルバーなので、両者の共通部分に真の解があることになります。計算時間はオリジナルが0.81secだったのに対してこちらは20.97secと、かなり遅くなってしまっています。Bünger先生によるとかなり高速化の工夫をしたとのことですが、これがMATLABの限界でしょうか。
Taylor model toolbox
こちらの最小限のコードはこんな感じだと思います。詳細はDEMOTAYLORMODEL Short demonstration of the Taylor model toolboxを見て下さい。
init = [1; 1];
[T,X,Xr] = verifyode(@vdp, [0, 20], init);
format long e
verifyode_disp(T,X,Xr,init);
function f = vdp(t, x, i)
mu = 1;
if nargin == 2 || isempty(i)
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
else
switch i
case 1
f = x(2);
case 2
f = mu*(1-x(1)^2)*x(2)-x(1);
end
end
end
こちらはawaの方にあったヤコビ行列を書く必要はありません。その代わり、右辺を定義する関数にt, xに続く第3の変数が増えており、そこに自然数が与えられたらその番号に対応する右辺の式だけを計算して返すことが要求されています。これも高速化のためです。関数verifyodeで計算した値をverifyode_dispで表示するのはAWA toolboxと同じですが、渡す変数の数がT, X, Xrと3つに増えており、またverifyode_dispには初期値も渡す必要があります。AWA toolboxと同様に
verifyodeset('order',12, 'h0',0,'loc_err_tol',1e-10,'shrinkwrap',1,'precondition',0,'blunting',0)
のようなオプションを第4引数に指定することによって動作をカスタマイズできます。AWAと違って非常にオプションが多く、またオプションの指定によって大きく性能が違うようなので、まずどんなオプションがいいか調べてみました。方程式は同じvan der Polでt=15まで計算、orderは18に固定して、区間幅の変化を調べてみました。それを行った結果が次のグラフです。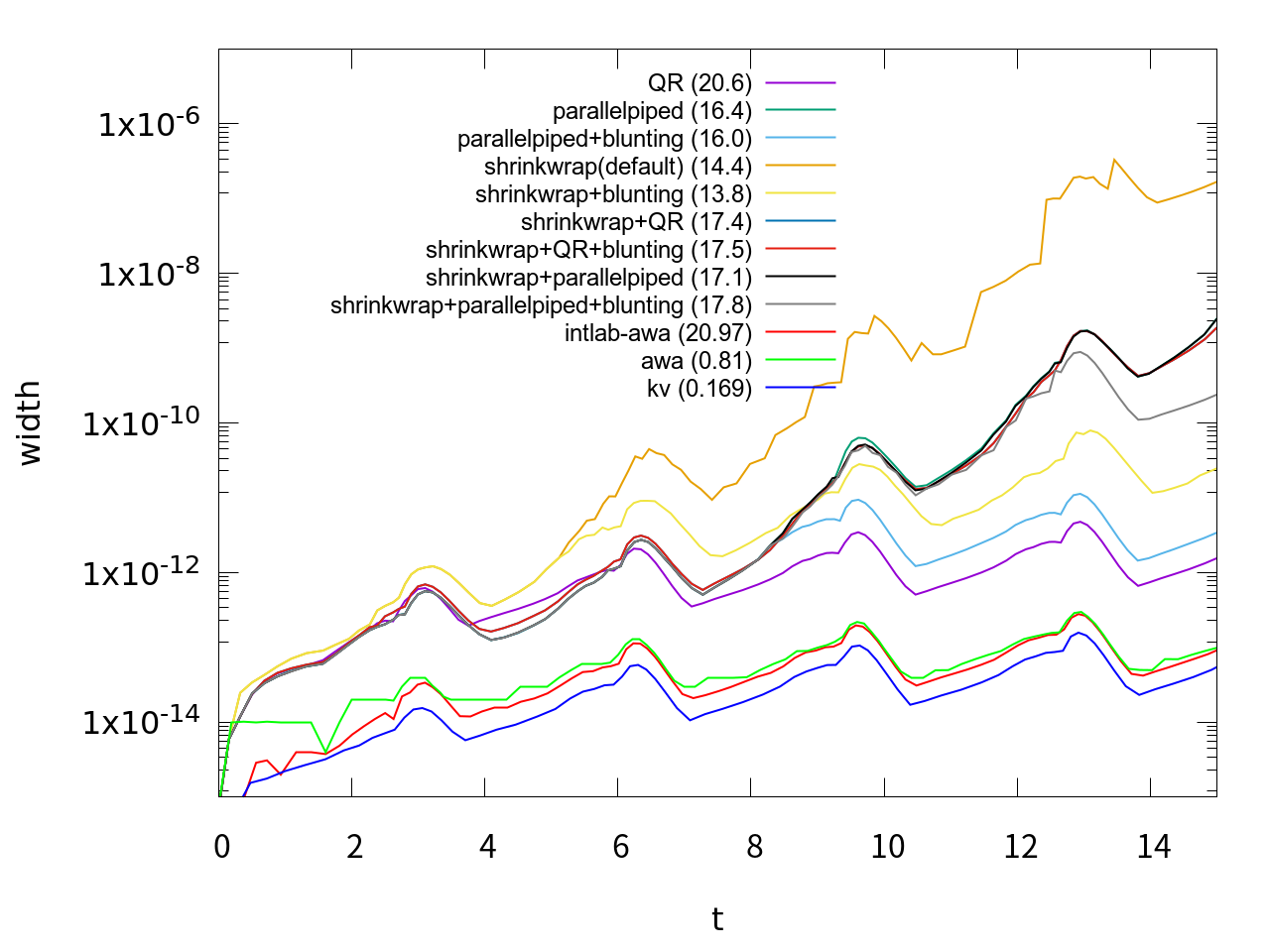
グラフの説明の上から9つが今回のTaylor Model Toolboxの計算結果で、下3つは他のもの(参考値)です。カッコ内の数値は計算時間(秒)です。グラフの説明は、それぞれ次のようなオプションと対応しています。横軸がt、縦軸は計算結果の区間幅を表しています。
| shrinkwrap | precondition | blunting | |
|---|---|---|---|
| QR | 0 | 1 | 0 |
| parallelpiped | 0 | 2 | 0 |
| parallelpiped + blunting | 0 | 2 | 1 |
| shrinkwrap(default) | 1 | 0 | 0 |
| shrinkwrap + blunting | 1 | 0 | 1 |
| shrinkwrap + QR | 1 | 1 | 0 |
| shrinkwrap + QR + blunting | 1 | 1 | 1 |
| shrinkwrap + parallelpiped | 1 | 2 | 0 |
| shrinkwrap + parallelpiped + blunting | 1 | 2 | 1 |
このパラメータを使い、更に次数を24に、loc_err_tolは1e-10に (いろいろ試すとこの数値が良かった) 設定して、以下を実行してみました。
init = [1; 1];
tic; [T,X,Xr] = verifyode(@vdp, [0, 20], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);
function f = vdp(t, x, i)
mu = 1;
if nargin == 2 || isempty(i)
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
else
switch i
case 1
f = x(2);
case 2
f = mu*(1-x(1)^2)*x(2)-x(1);
end
end
end
すると、次のような解が得られました。
経過時間は 24.897000 秒です。
t = 0
[y_1] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_1]) = 0.00e+00
[y_2] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_2]) = 0.00e+00
t = 2.218563039351837e-01
[y_1] = [ 1.192420354444434e+000, 1.192420354444441e+000] d([y_1]) = 5.77e-15
[y_2] = [ 7.162286750812696e-001, 7.162286750812727e-001] d([y_2]) = 2.89e-15
(中略)
t = 1.986588757581453e+01
[y_1] = [ 1.983929113336597e+000, 1.983929113337129e+000] d([y_1]) = 5.31e-13
[y_2] = [ 3.648228353937841e-001, 3.648228353977482e-001] d([y_2]) = 3.96e-12
t = 20
[y_1] = [ 2.008487917798372e+000, 2.008487917798472e+000] d([y_1]) = 9.95e-14
[y_2] = [ 2.328985430522710e-002, 2.328985430793645e-002] d([y_2]) = 2.71e-12
少し精度が落ちているものの、同様に精度保証された解が得られました。計算時間は25秒弱とやや遅めです。Taylor model toolboxに指定した
verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)
は試行錯誤の結果ですが、もっと良い設定があるかもしれません。情報は募集中です。当然、方程式や初期値が違えばまた最適値も変わる可能性が高いです。Taylor modelは前評判からするとやや性能が出ておらず、少しがっかりしています。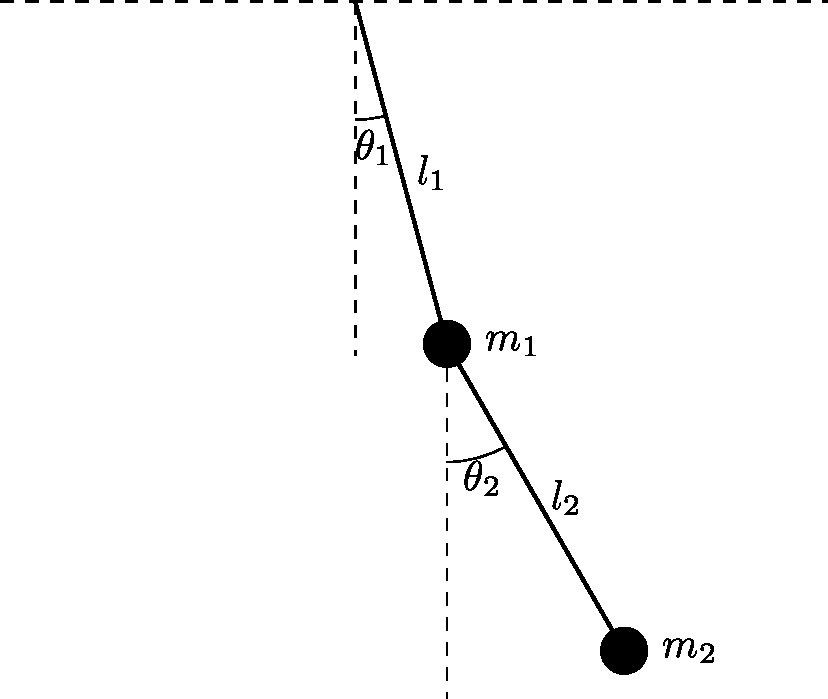二重振り子の精度保証付き数値計算で勝負
最後に、二重振り子の精度保証付き数値計算の記事の二重振り子の軌道を計算させてみて、AWA, kvライブラリと比較してみました。
使った式は、以前と同じ
\begin{align*}
& (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)
+ m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)
+(m_1+m_2)g \sin \theta_1= 0 \\
& l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2}
-l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0
\end{align*}
\begin{align*}
m_1 &= m_2 = 1 \\
l_1 &= l_2 = 1 \\
g &= 9.8 \\
\end{align*}
\begin{align*}
\theta_1(0) &= \frac{3}{4}\pi \\
\theta_2(0) &= \frac{3}{4}\pi \\
\dot{\theta_1}(0) &= 0 \\
\dot{\theta_2}(0) &= 0
\end{align*}
です。使用したプログラムは、Taylor model toolboxが、
init = [intval('pi')*0.75; intval('pi')*0.75; 0; 0];
tic; [T,X,Xr] = verifyode(@doublependulum, [0, 11], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);
function f = doublependulum(t, x, i)
persistent g;
if (isempty(g))
g = intval('9.8');
end
m1 = 1;
m2 = 1;
l1 = 1;
l2 = 1;
t1 = cos(x(1) - x(2));
t2 = sin(x(1) - x(2));
a = (m1 + m2) * l1;
b = m2 * l2 * t1;
c = l1 * l2 * t1;
d = l2 * l2;
dt = a*d - b*c;
v1 = -m2 * l2 * x(4) * x(4) * t2 - (m1 + m2) * g * sin(x(1));
v2 = l1 * l2 * x(3) * x(3) * t2 - g * l2 * sin(x(2));
if nargin == 2 || isempty(i)
f = [x(3);
x(4);
(d * v1 - b * v2) / dt;
(-c * v1 + a * v2) / dt];
else
switch i
case 1
f = x(3);
case 2
f = x(4);
case 3
f = (d * v1 - b * v2) / dt;
case 4
f = (-c * v1 + a * v2) / dt;
end
end
end
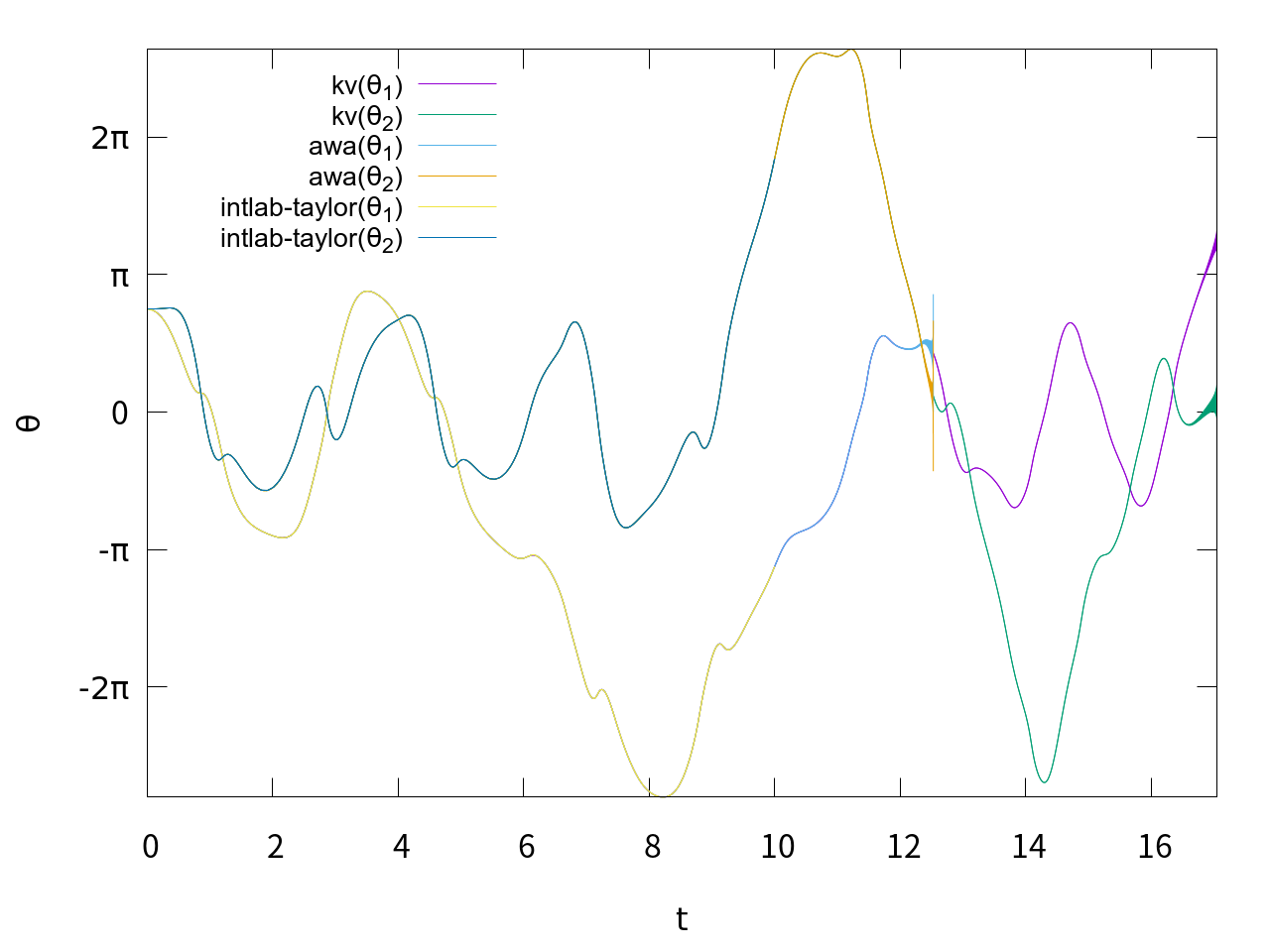
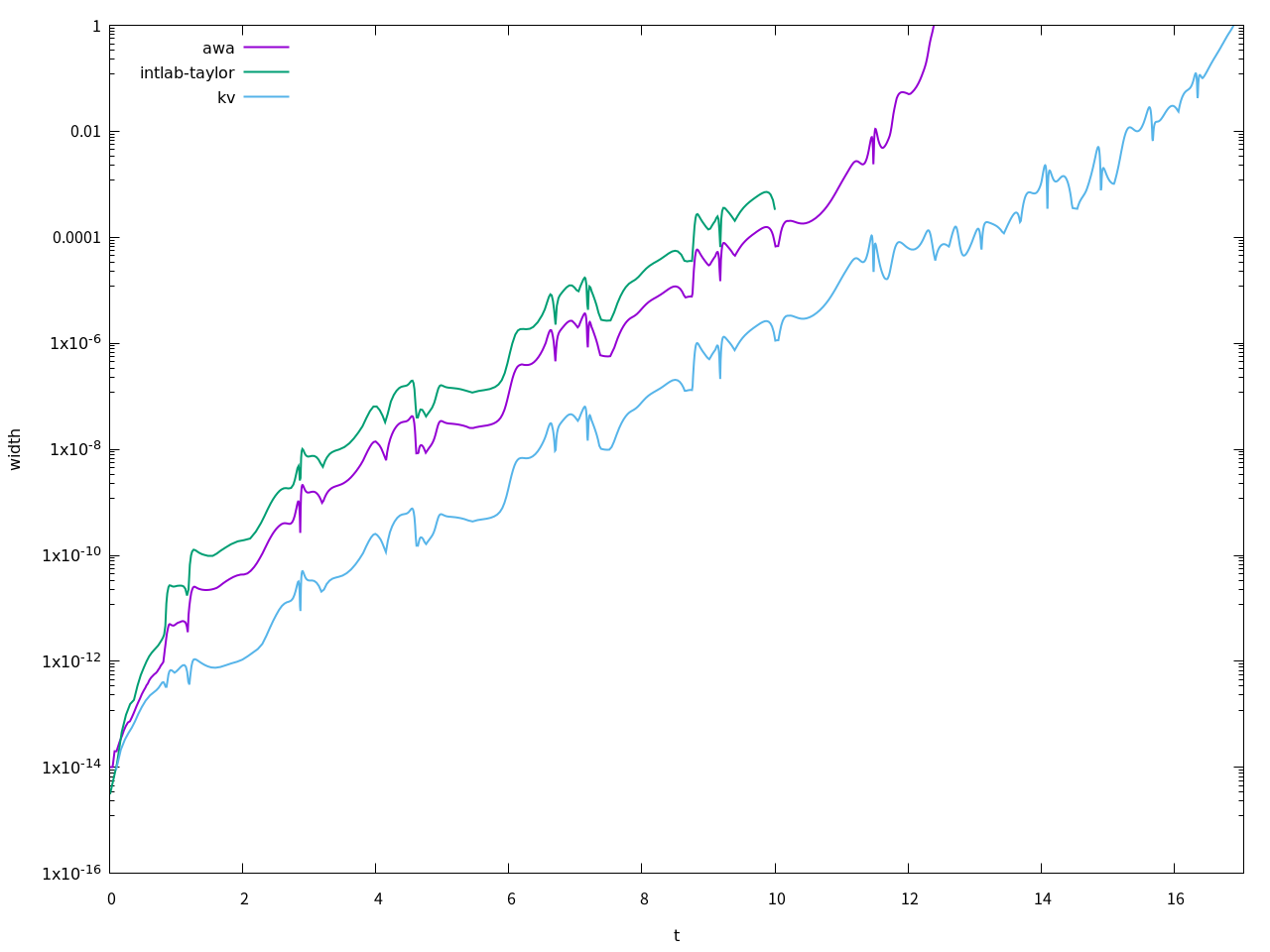
AWAが、M1 = 1 M2 = 1 L1 = 1 L2 = 1 G = 9.8 T1 = cos(U1 - U2) T2 = sin(U1 - U2) A = (M1 + M2) * L1 B = M2 * L2 * T1 C = L1 * L2 * T1 D = L2 * L2 DT = A*D - B*C V1 = -M2 * L2 * U4 * U4 * T2 - (M1 + M2) * G * sin(U1) V2 = L1 * L2 * U3 * U3 * T2 - G * L2 * sin(U2) F1 = U3 F2 = U4 F3 = ( D*V1 - B*V2) / DT F4 = (-C*V1 + A*V2) / DT ;; 1 0 13 0 24 4 0 [2.35619449019234492884698253745961,2.356194490192344928846982537459636] [2.35619449019234492884698253745961,2.356194490192344928846982537459636] 0 0 n 1e-16 1e-16kvが、
#include <iostream>
#include <limits>
#include <kv/ode-maffine.hpp>
#include <kv/constants.hpp>
#include <kv/ode-callback.hpp>
namespace ub = boost::numeric::ublas;
typedef kv::interval<double> itv;
struct DoublePendulum {
template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
ub::vector<T> y(4);
ub::matrix<T> tm(2,2);
ub::vector<T> tv(2);
T a, b, c, d, t1, t2;
static const T m1 = T(1.);
static const T m2 = T(1.);
static const T l1 = T(1.);
static const T l2 = T(1.);
static const T g = kv::constants<T>::str("9.8");
t1 = cos(x(0) - x(1));
t2 = sin(x(0) - x(1));
a = (m1 + m2) * l1;
b = m2 * l2 * t1;
c = l1 * l2 * t1;
d = l2 * l2;
tm(0,0) = d;
tm(0,1) = -b;
tm(1,0) = -c;
tm(1,1) = a;
tm /= (a*d - b*c);
tv(0) = -m2 * l2 * x(3) * x(3) * t2 - (m1 + m2) * g * sin(x(0));
tv(1) = l1 * l2 * x(2) * x(2) * t2 - g * l2 * sin(x(1));
tv = prod(tm, tv);
y(0) = x(2);
y(1) = x(3);
y(2) = tv(0);
y(3) = tv(1);
return y;
}
};
int main()
{
ub::vector<itv> ix;
itv end;
std::cout.precision(17);
ix.resize(4);
ix(0) = 0.75 * kv::constants<itv>::pi();
ix(1) = 0.75 * kv::constants<itv>::pi();
ix(2) = 0.;
ix(3) = 0.;
// end = std::numeric_limits<double>::infinity();
end = 17.05;
kv::odelong_maffine(DoublePendulum(), ix, itv(0.), end, kv::ode_param<itv::base_type>().set_verbose(1));
}
です。IntlabのAWA toolboxは、関数のヤコビ行列を書くのが面倒で試しませんでした。計算結果を図示します。
このようになりました。さすがは精度保証付きソルバー、当たり前ではありますがグラフがぴったり重なっています。Taylor model toolboxはt=10までは計算できましたが、t=11では計算が止まりませんでした。AWAはt=12過ぎで解が発散しました。kvはt=17過ぎまで計算できました。解の区間幅を図示すると、
このようになりました。kvが長い時間区間幅が発散せずに持ちこたえていることが分かります。
計算時間は、全員が計算可能なt=10までで、Taylor model toolboxが5時間20分17秒、AWAが17.9秒、kvが22.9秒でした。
kvは、他の2つには不可能な、内部の演算型を全てdouble-double(疑似4倍精度)に変えて精度保証付き計算を行うこともでき、この場合は軽々とt=30以上まで計算することができます。