2018/12/09(日)Intlab 11の精度保証付きODE Solver
一つは、先ごろ紹介したLohnerのAWAを移植したAWA Toolboxです。AWAはPascal-XSCというマイナーな言語で書かれていますから、メジャーなMATLABで書かれていた方がありがたい、という人もいるでしょう。
もう一つは、Berz, Makinoによる精度保証付き初期値問題ソルバーCOSY INFINITYを移植した Taylor model toolbox です。解を初期値に関して高次に展開することによる非常に高性能な精度保証付きアルゴリズムとして知られています。
今回は、この両者を実際に動かしてみたレポートです。MATLABはLinux上でR2018aを使いました。
まずはIntlab 11を買います。PayPalで支払うと、メールで6時間有効なダウンロードリンクが送られてくるので、INTLAB.zipをダウンロードしておきましょう。中身のファイルそのものは特にプロテクトがかかっているわけではなく自由に使えます。Intlabのインストールは簡単で、zipを解凍して好きなディレクトリに置くだけです。Intlabの機能を使う前に、MATLABでそのディレクトリにcdして startintlab とタイプします。初回はいろいろ調査するため時間がかかります。注意点は、IntlabはMATLABとoctave(MATLAB互換フリーソフト)に対応していますが、残念ながら精度保証付き初期値問題のためのAWA toolboxとTaylor model toolboxはoctaveに対応していません。octaveでのテストを行わずに開発していたそうで、またいくつかのoctaveの非互換の部分が問題ですぐに対応するのは難しいそうです。
次に実際に動かしてみます。例題は、以前LohnerのAWAを紹介した記事と同じ、van der Pol方程式:
\begin{align*}
\frac{dx}{dt} &= y \\
\frac{dy}{dt} &= \mu (1-x^2)y - x
\end{align*}
で、\mu=1とし、初期値 (x(0),y(0))=(1,1)でt\in[0,20]の範囲で計算する問題にしました。AWA toolbox
まずAWA toolboxの方の使い方を説明します。詳細はDEMOAWA Short demonstration of the AWA toolboxのページを見て下さい。最小限のコードはこんな感じだと思います。これを適当な名前 (例えばhoge.m) でファイルを作成し、MATLAB上でhogeで実行できます。
init = [1; 1];
[T,X] = awa(@vdp, @vdp_J, [0, 20], init);
format long e
awa_disp(T,X);
function f = vdp(t, x)
mu = 1;
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
end
function J = vdp_J(t, x)
mu = 1;
J = [typeadjust(0, x), typeadjust(1, x);
-2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end
このように、ODEの右辺を定義する関数(ここではvdp)と、そのヤコビ行列を返す関数(ここではvdp_J)を定義し、関数awaを呼びます。awaの計算したデータを分かりやすく表示してくれるのがawa_dispです。ヤコビ行列を定義するのが面倒ですし、Intlabの持っている自動微分機能でなんとかなりそうな気がするのですが、高速化のためにやむを得なかったそうです。typeadjustという関数が使われていますが、関数の戻り値に定数があるときはこうやって型を補正する必要があります。更に、関数awaの第5引数に
awaset('order',10,'h0',0,'EvalMeth',4,'AbsTol',1e-16,'RelTol',1e-16)
のような関数を使って、様々なパラメータを変更することができます(これらの値はデフォルト値)。変更したいパラメータの名前を奇数番目の引数に、値を偶数番目の引数に書きます。これを使って、LohnerのAWAを紹介した記事に合わせてTaylor展開の次数を24次にした、
init = [1; 1];
tic; [T,X] = awa(@vdp, @vdp_J, [0, 20], init, awaset('order', 24)); toc
format long e
awa_disp(T,X);
function f = vdp(t, x)
mu = 1;
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
end
function J = vdp_J(t, x)
mu = 1;
J = [typeadjust(0, x), typeadjust(1, x);
-2*mu*x(1)*x(2) - 1, mu*(1-x(1)^2)];
end
を実行してみました。すると、次のような解が得られました。
経過時間は 20.973900 秒です。
t = 0
[y_1] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_1]) = 0.00e+00
[y_2] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_2]) = 0.00e+00
t = 1.911224186649680e-01
[y_1] = [ 1.169708666105268e+000, 1.169708666105269e+000] d([y_1]) = 6.66e-16
[y_2] = [ 7.615010659752849e-001, 7.615010659752856e-001] d([y_2]) = 4.44e-16
(中略)
t = 1.992657858092985e+01
[y_1] = [ 2.000739935214436e+000, 2.000739935214461e+000] d([y_1]) = 2.31e-14
[y_2] = [ 1.939352117515359e-001, 1.939352117517785e-001] d([y_2]) = 2.42e-13
t = 20
[y_1] = [ 2.008487917798417e+000, 2.008487917798427e+000] d([y_1]) = 7.99e-15
[y_2] = [ 2.328985430648321e-002, 2.328985430667890e-002] d([y_2]) = 1.96e-13
オリジナルのAWAのt=20における解は、t = 2.000000000000000E+001 [ 2.00848791779841E+000, 2.00848791779843E+000] 8.00E-015 4.0E-015 [ 2.32898543064796E-002, 2.32898543066811E-002] 2.02E-013 8.7E-012でした。どちらも精度保証付きソルバーなので、両者の共通部分に真の解があることになります。計算時間はオリジナルが0.81secだったのに対してこちらは20.97secと、かなり遅くなってしまっています。Bünger先生によるとかなり高速化の工夫をしたとのことですが、これがMATLABの限界でしょうか。
Taylor model toolbox
こちらの最小限のコードはこんな感じだと思います。詳細はDEMOTAYLORMODEL Short demonstration of the Taylor model toolboxを見て下さい。
init = [1; 1];
[T,X,Xr] = verifyode(@vdp, [0, 20], init);
format long e
verifyode_disp(T,X,Xr,init);
function f = vdp(t, x, i)
mu = 1;
if nargin == 2 || isempty(i)
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
else
switch i
case 1
f = x(2);
case 2
f = mu*(1-x(1)^2)*x(2)-x(1);
end
end
end
こちらはawaの方にあったヤコビ行列を書く必要はありません。その代わり、右辺を定義する関数にt, xに続く第3の変数が増えており、そこに自然数が与えられたらその番号に対応する右辺の式だけを計算して返すことが要求されています。これも高速化のためです。関数verifyodeで計算した値をverifyode_dispで表示するのはAWA toolboxと同じですが、渡す変数の数がT, X, Xrと3つに増えており、またverifyode_dispには初期値も渡す必要があります。AWA toolboxと同様に
verifyodeset('order',12, 'h0',0,'loc_err_tol',1e-10,'shrinkwrap',1,'precondition',0,'blunting',0)
のようなオプションを第4引数に指定することによって動作をカスタマイズできます。AWAと違って非常にオプションが多く、またオプションの指定によって大きく性能が違うようなので、まずどんなオプションがいいか調べてみました。方程式は同じvan der Polでt=15まで計算、orderは18に固定して、区間幅の変化を調べてみました。それを行った結果が次のグラフです。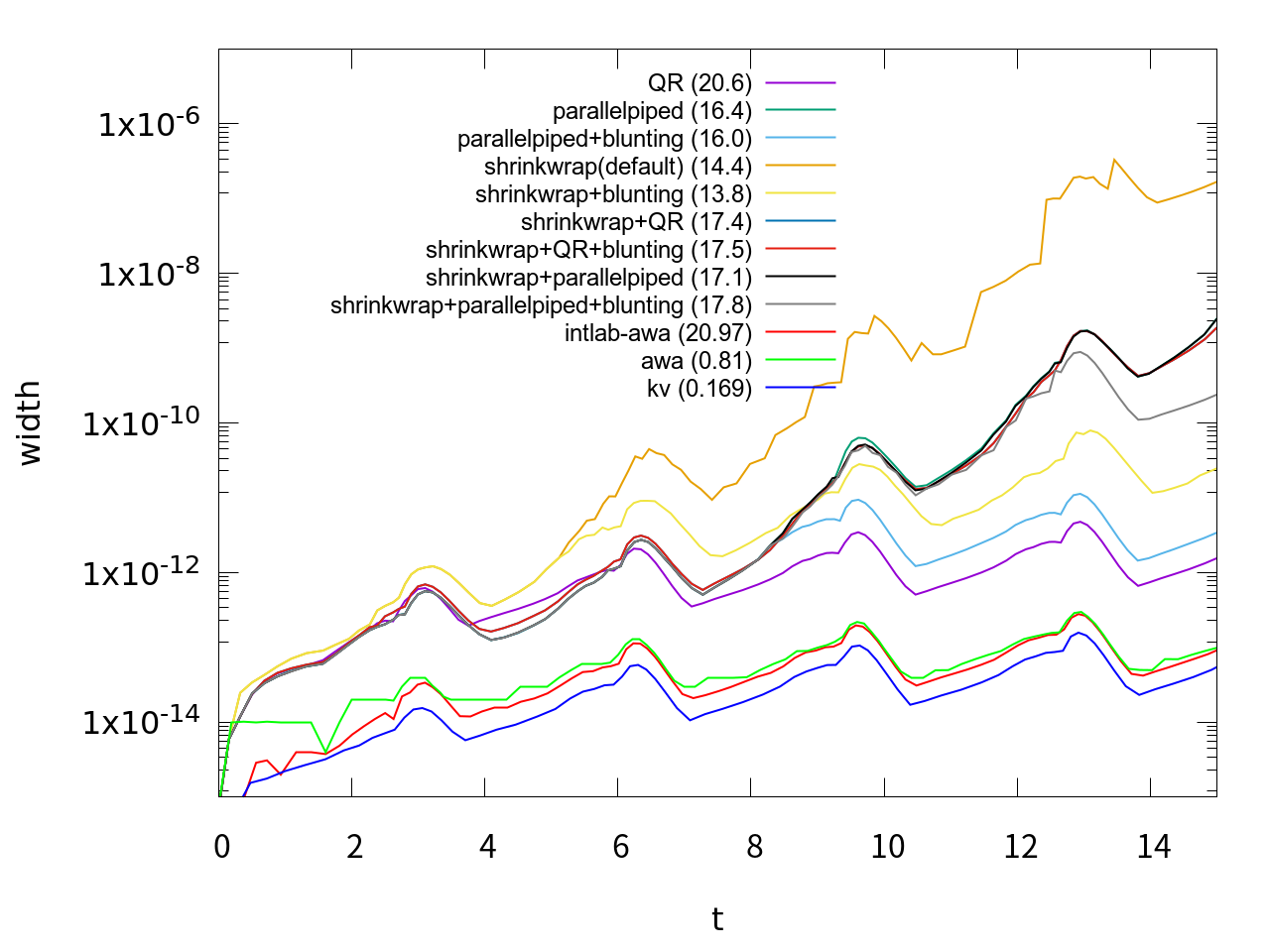
グラフの説明の上から9つが今回のTaylor Model Toolboxの計算結果で、下3つは他のもの(参考値)です。カッコ内の数値は計算時間(秒)です。グラフの説明は、それぞれ次のようなオプションと対応しています。横軸がt、縦軸は計算結果の区間幅を表しています。
| shrinkwrap | precondition | blunting | |
|---|---|---|---|
| QR | 0 | 1 | 0 |
| parallelpiped | 0 | 2 | 0 |
| parallelpiped + blunting | 0 | 2 | 1 |
| shrinkwrap(default) | 1 | 0 | 0 |
| shrinkwrap + blunting | 1 | 0 | 1 |
| shrinkwrap + QR | 1 | 1 | 0 |
| shrinkwrap + QR + blunting | 1 | 1 | 1 |
| shrinkwrap + parallelpiped | 1 | 2 | 0 |
| shrinkwrap + parallelpiped + blunting | 1 | 2 | 1 |
このパラメータを使い、更に次数を24に、loc_err_tolは1e-10に (いろいろ試すとこの数値が良かった) 設定して、以下を実行してみました。
init = [1; 1];
tic; [T,X,Xr] = verifyode(@vdp, [0, 20], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);
function f = vdp(t, x, i)
mu = 1;
if nargin == 2 || isempty(i)
f = [x(2);
mu*(1-x(1)^2)*x(2)-x(1)];
else
switch i
case 1
f = x(2);
case 2
f = mu*(1-x(1)^2)*x(2)-x(1);
end
end
end
すると、次のような解が得られました。
経過時間は 24.897000 秒です。
t = 0
[y_1] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_1]) = 0.00e+00
[y_2] = [ 1.000000000000000e+000, 1.000000000000000e+000] d([y_2]) = 0.00e+00
t = 2.218563039351837e-01
[y_1] = [ 1.192420354444434e+000, 1.192420354444441e+000] d([y_1]) = 5.77e-15
[y_2] = [ 7.162286750812696e-001, 7.162286750812727e-001] d([y_2]) = 2.89e-15
(中略)
t = 1.986588757581453e+01
[y_1] = [ 1.983929113336597e+000, 1.983929113337129e+000] d([y_1]) = 5.31e-13
[y_2] = [ 3.648228353937841e-001, 3.648228353977482e-001] d([y_2]) = 3.96e-12
t = 20
[y_1] = [ 2.008487917798372e+000, 2.008487917798472e+000] d([y_1]) = 9.95e-14
[y_2] = [ 2.328985430522710e-002, 2.328985430793645e-002] d([y_2]) = 2.71e-12
少し精度が落ちているものの、同様に精度保証された解が得られました。計算時間は25秒弱とやや遅めです。Taylor model toolboxに指定した
verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)
は試行錯誤の結果ですが、もっと良い設定があるかもしれません。情報は募集中です。当然、方程式や初期値が違えばまた最適値も変わる可能性が高いです。Taylor modelは前評判からするとやや性能が出ておらず、少しがっかりしています。二重振り子の精度保証付き数値計算で勝負
最後に、二重振り子の精度保証付き数値計算の記事の二重振り子の軌道を計算させてみて、AWA, kvライブラリと比較してみました。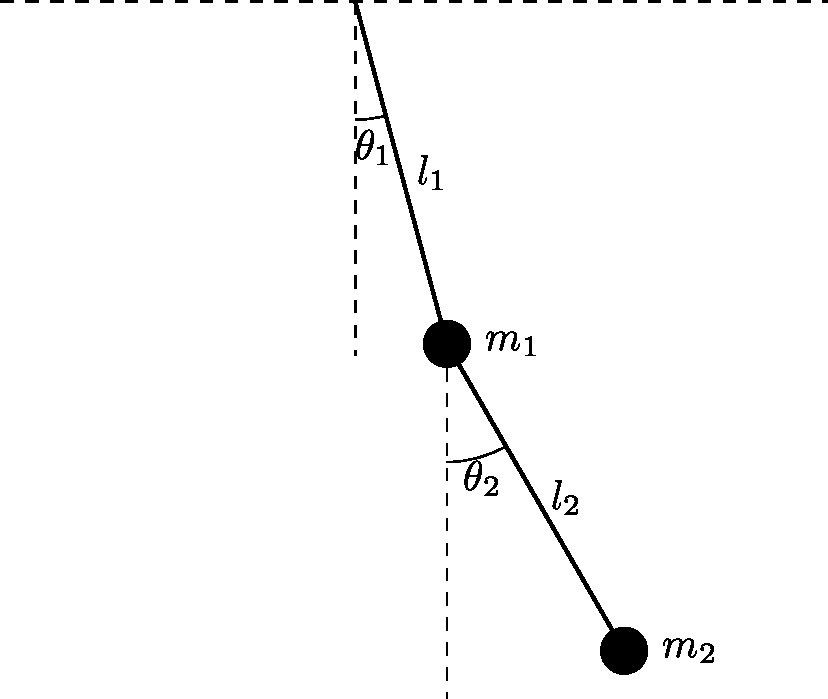
使った式は、以前と同じ
\begin{align*}
& (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)
+ m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)
+(m_1+m_2)g \sin \theta_1= 0 \\
& l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2}
-l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0
\end{align*}
\begin{align*}
m_1 &= m_2 = 1 \\
l_1 &= l_2 = 1 \\
g &= 9.8 \\
\end{align*}
\begin{align*}
\theta_1(0) &= \frac{3}{4}\pi \\
\theta_2(0) &= \frac{3}{4}\pi \\
\dot{\theta_1}(0) &= 0 \\
\dot{\theta_2}(0) &= 0
\end{align*}
です。使用したプログラムは、Taylor model toolboxが、
init = [intval('pi')*0.75; intval('pi')*0.75; 0; 0];
tic; [T,X,Xr] = verifyode(@doublependulum, [0, 11], init, verifyodeset('order', 24, 'loc_err_tol', 1e-10, 'shrinkwrap', 0, 'precondition', 1, 'blunting', 0)); toc;
format long e
verifyode_disp(T,X,Xr,init);
function f = doublependulum(t, x, i)
persistent g;
if (isempty(g))
g = intval('9.8');
end
m1 = 1;
m2 = 1;
l1 = 1;
l2 = 1;
t1 = cos(x(1) - x(2));
t2 = sin(x(1) - x(2));
a = (m1 + m2) * l1;
b = m2 * l2 * t1;
c = l1 * l2 * t1;
d = l2 * l2;
dt = a*d - b*c;
v1 = -m2 * l2 * x(4) * x(4) * t2 - (m1 + m2) * g * sin(x(1));
v2 = l1 * l2 * x(3) * x(3) * t2 - g * l2 * sin(x(2));
if nargin == 2 || isempty(i)
f = [x(3);
x(4);
(d * v1 - b * v2) / dt;
(-c * v1 + a * v2) / dt];
else
switch i
case 1
f = x(3);
case 2
f = x(4);
case 3
f = (d * v1 - b * v2) / dt;
case 4
f = (-c * v1 + a * v2) / dt;
end
end
end
AWAが、M1 = 1 M2 = 1 L1 = 1 L2 = 1 G = 9.8 T1 = cos(U1 - U2) T2 = sin(U1 - U2) A = (M1 + M2) * L1 B = M2 * L2 * T1 C = L1 * L2 * T1 D = L2 * L2 DT = A*D - B*C V1 = -M2 * L2 * U4 * U4 * T2 - (M1 + M2) * G * sin(U1) V2 = L1 * L2 * U3 * U3 * T2 - G * L2 * sin(U2) F1 = U3 F2 = U4 F3 = ( D*V1 - B*V2) / DT F4 = (-C*V1 + A*V2) / DT ;; 1 0 13 0 24 4 0 [2.35619449019234492884698253745961,2.356194490192344928846982537459636] [2.35619449019234492884698253745961,2.356194490192344928846982537459636] 0 0 n 1e-16 1e-16kvが、
#include <iostream>
#include <limits>
#include <kv/ode-maffine.hpp>
#include <kv/constants.hpp>
#include <kv/ode-callback.hpp>
namespace ub = boost::numeric::ublas;
typedef kv::interval<double> itv;
struct DoublePendulum {
template <class T> ub::vector<T> operator() (const ub::vector<T>& x, T t){
ub::vector<T> y(4);
ub::matrix<T> tm(2,2);
ub::vector<T> tv(2);
T a, b, c, d, t1, t2;
static const T m1 = T(1.);
static const T m2 = T(1.);
static const T l1 = T(1.);
static const T l2 = T(1.);
static const T g = kv::constants<T>::str("9.8");
t1 = cos(x(0) - x(1));
t2 = sin(x(0) - x(1));
a = (m1 + m2) * l1;
b = m2 * l2 * t1;
c = l1 * l2 * t1;
d = l2 * l2;
tm(0,0) = d;
tm(0,1) = -b;
tm(1,0) = -c;
tm(1,1) = a;
tm /= (a*d - b*c);
tv(0) = -m2 * l2 * x(3) * x(3) * t2 - (m1 + m2) * g * sin(x(0));
tv(1) = l1 * l2 * x(2) * x(2) * t2 - g * l2 * sin(x(1));
tv = prod(tm, tv);
y(0) = x(2);
y(1) = x(3);
y(2) = tv(0);
y(3) = tv(1);
return y;
}
};
int main()
{
ub::vector<itv> ix;
itv end;
std::cout.precision(17);
ix.resize(4);
ix(0) = 0.75 * kv::constants<itv>::pi();
ix(1) = 0.75 * kv::constants<itv>::pi();
ix(2) = 0.;
ix(3) = 0.;
// end = std::numeric_limits<double>::infinity();
end = 17.05;
kv::odelong_maffine(DoublePendulum(), ix, itv(0.), end, kv::ode_param<itv::base_type>().set_verbose(1));
}
です。IntlabのAWA toolboxは、関数のヤコビ行列を書くのが面倒で試しませんでした。計算結果を図示します。
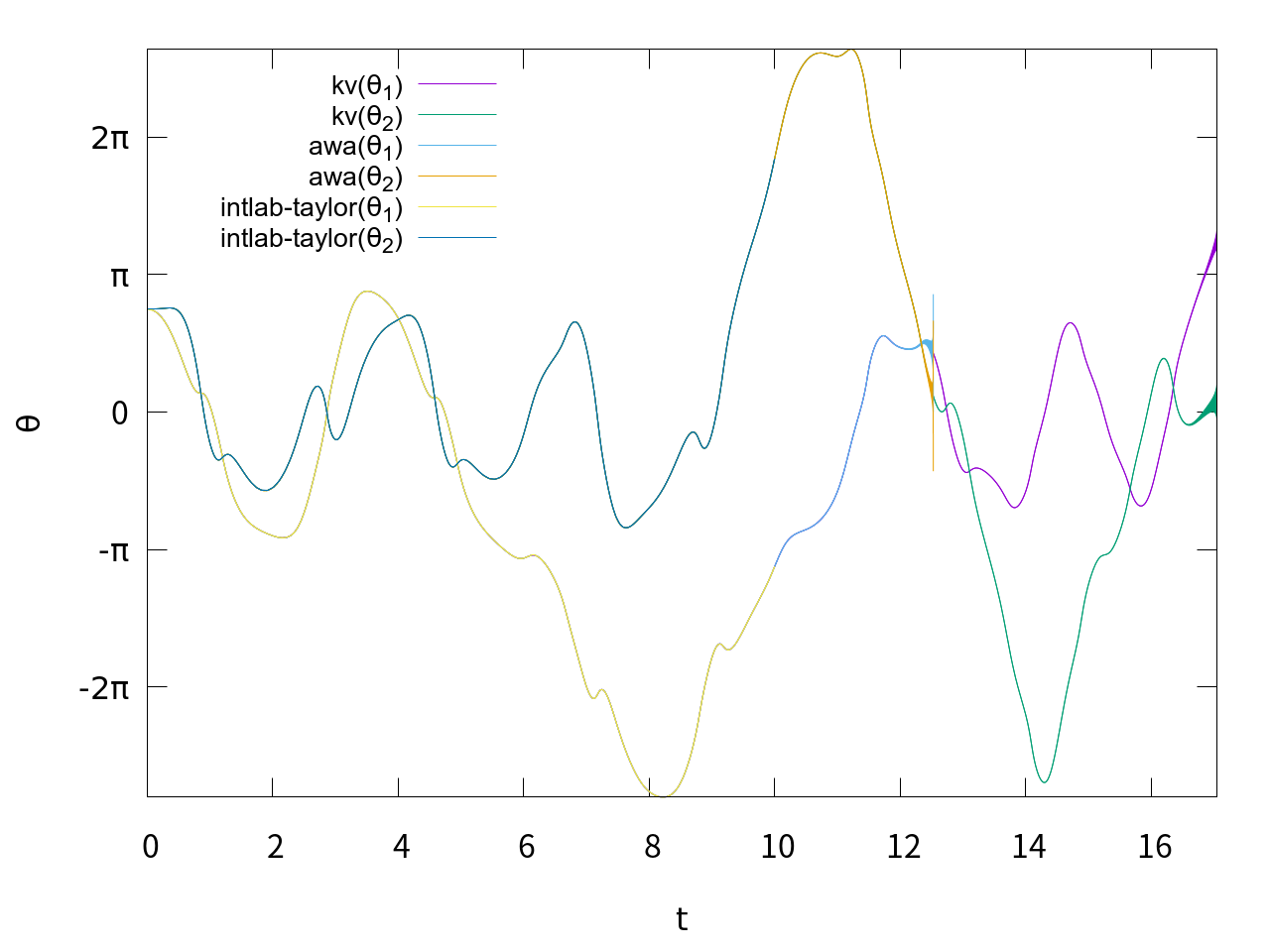
このようになりました。さすがは精度保証付きソルバー、当たり前ではありますがグラフがぴったり重なっています。Taylor model toolboxはt=10までは計算できましたが、t=11では計算が止まりませんでした。AWAはt=12過ぎで解が発散しました。kvはt=17過ぎまで計算できました。解の区間幅を図示すると、
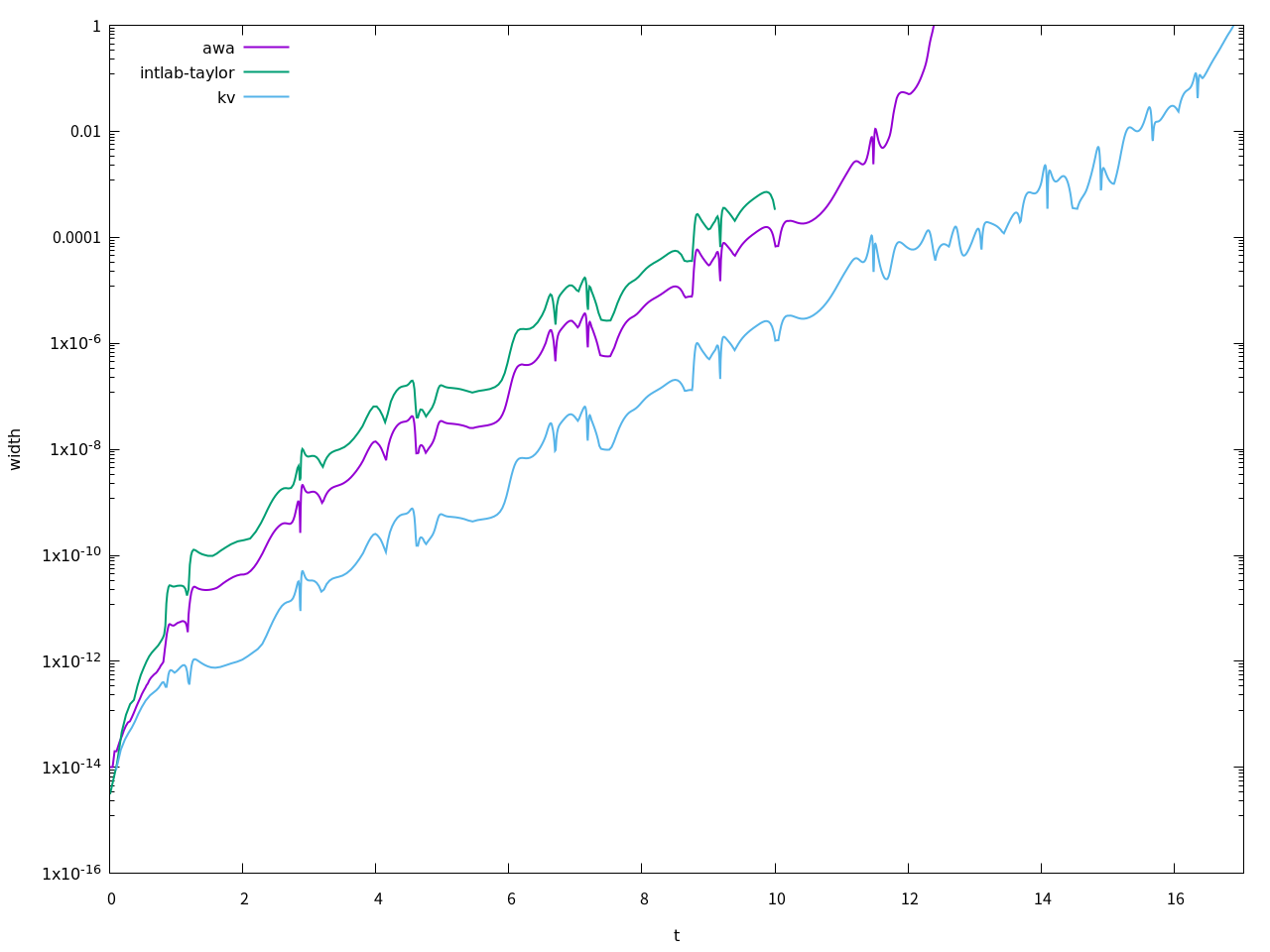
このようになりました。kvが長い時間区間幅が発散せずに持ちこたえていることが分かります。
計算時間は、全員が計算可能なt=10までで、Taylor model toolboxが5時間20分17秒、AWAが17.9秒、kvが22.9秒でした。
kvは、他の2つには不可能な、内部の演算型を全てdouble-double(疑似4倍精度)に変えて精度保証付き計算を行うこともでき、この場合は軽々とt=30以上まで計算することができます。
2018/09/10(月)「精度保証付き数値計算の基礎」チュートリアル
精度保証付き数値計算の基礎
という本を出しました。私が執筆したのは、第4章「数学関数の精度保証」と、第7章「常微分方程式の精度保証付き数値解法」です。
で、今回、
「精度保証付き数値計算の基礎」チュートリアル
で話させていただきました。そこで使ったスライドを上げておきます。内容は第4章の数学関数の精度保証の話で、発表時間は20分だったので、簡単な内容です。割と多くの方に来ていただいてとても嬉しかったです。
なお、今回のチュートリアルは6章までで、7章のODEと8章のPDEについては年末に別の機会を準備中です。
2017/08/08(火)二重振り子の精度保証付き数値計算
わずかに異なる初期値をもった50本の二重振り子のシミュレーションを動画にしたもので、途中まで完全に重なっているように見える振り子が一気にバラける様子がとても面白い。
次は、それを三重振り子にしたもの。
gmpを用いて高精度計算をしており、ねとらぼで記事にもなりました。
どちらも常微分方程式の計算にはルンゲクッタ法を用いています。わずかな初期値のずれが後に大きな違いをもたらすことがとてもよく分かる動画ですが、一方で、ルンゲクッタ法で計算された値も真値とはわずかにずれており、当然その誤差も同様に後で大きな違いをもたらすことになります。だとすると、果たして意味のある計算になっているのかという疑問が生じます。
そこで、二重振り子の軌道を精度保証付きで計算し、ルンゲクッタ法とどのくらいずれるのか検証してみました。そのtweetがこれです。
このように、4次のルンゲクッタ法(刻み幅2^{-7})と精度保証付き計算とを比較してみると、t=8あたりから先は完全に違う軌道になってしまっていることが分かりました。
以下では、twitterに書けなかった細かい情報を備忘録も兼ねて書いておこうと思います。
使った式は、
\begin{align*}
& (m_1+m_2)l_1\ddot{\theta_1} + m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)
+ m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)
+(m_1+m_2)g \sin \theta_1= 0 \\
& l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2) + l_2^2\ddot{\theta_2}
-l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) + g l_2 \sin \theta_2= 0
\end{align*}
のようなものです(Wikipediaの記事と全く同じです)。舞台設定は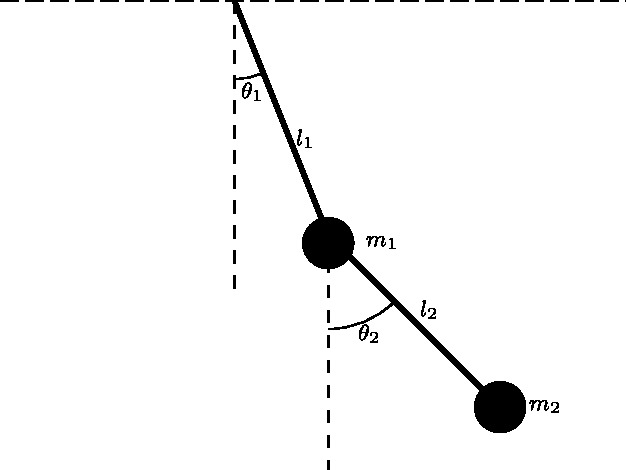
の通り。この式を\ddot{\theta_1}, \ddot{\theta_2}の2変数連立一次方程式と見て解いて正規形に直し、\dot{\theta_1}=\phi_1, \dot{\theta_2}=\phi_2のように置き直して1階4変数の常微分方程式とします。パラメータは
\begin{align*}
m_1 &= m_2 = 1 \\
l_1 &= l_2 = 1 \\
g &= 9.8 \\
\end{align*}
とし、初期値は
\begin{align*}
\theta_1(0) &= \frac{3}{4}\pi \\
\theta_2(0) &= \frac{3}{4}\pi \\
\dot{\theta_1}(0) &= 0 \\
\dot{\theta_2}(0) &= 0
\end{align*}
としました。kvライブラリを用いて、この初期値問題を精度保証付きで計算するプログラムと、4次のルンゲクッタ法で計算するプログラムを書きました。両方のプログラムをzipで上げておきます ( doublependulum.zip )。4次のルンゲクッタ法の刻み幅は固定で2^{-7}としました。精度保証付きの方は全ての時刻の解を多項式の形で連続的に計算しているのですが、ルンゲクッタ法と同じ2^{-7}の刻み幅で密出力させています。この計算結果を動画にしたものが、先のtweetというわけです。
プログラムを走らせて得られた生データを上げておきます ( doublependulum-result.zip )。t=1のときの両プログラムのデータを抜き出すと、
| \theta_1 | \theta_2 | |
|---|---|---|
| kv | [ 0.14046540255551162,0.14046540255558421] | [ -0.71766989300731332,-0.71766989300724726] |
| rk4 | 0.1404652582264235 | -0.71766977132932186 |
このデータをグラフにしてみました。
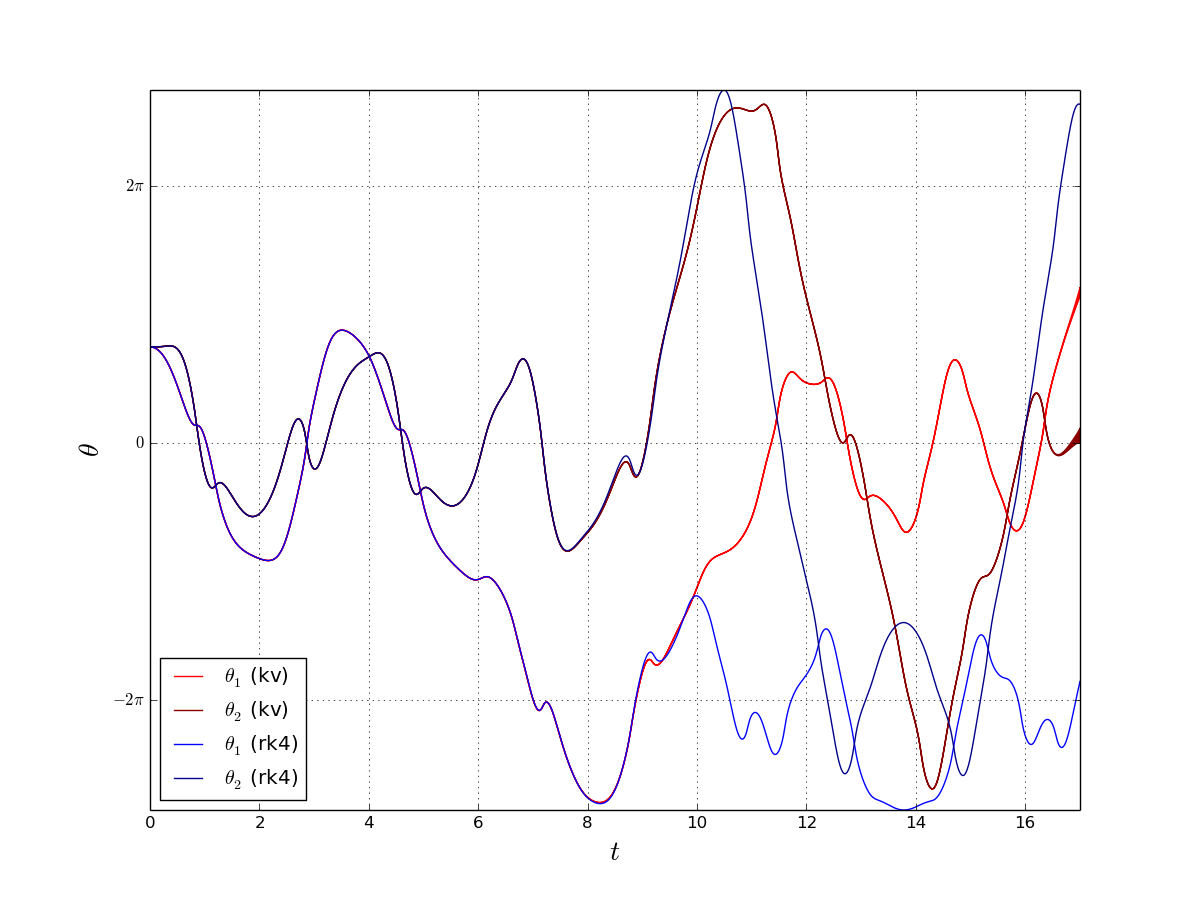
t=8付近でずれが目に見えるようになり、そのあとは完全に異なる軌道を描いています。
精度保証付き計算もいつまでも高精度を保っていられるわけではなく、t=17付近を見るとわずかにグラフに幅があるのが分かります。この後一気に区間幅が爆発し、t=17.05付近で計算不能に陥ります。この精度保証付き計算プログラムはgmpのような高精度数を使用しているわけではなく、内部で使っているのは普通のdoubleです。試しに内部の数値型をdd(擬似4倍精度数)に変えてみたところ、t=30くらいまでは普通に破綻すること無く計算出来ました。
二重振り子の動画を見るだけなら、精度保証してもしなくても動きの「印象」はほとんど変わらないのですが、カオス系に対して数値シミュレーションで何らかの数学的な結論を得ようと思うならば、誤差が明確に把握できる精度保証付き数値計算は必須だと思います。みなさま、精度保証付き数値計算を使いましょう!
2015/10/15(木)MATLAB 2015b での精度保証
- BLASを他のものに差し替える。速度は遅くなってしまうことが多い。
- matlabを2012aで留めておく。
- マルチコア使用を禁止し、シングルコアで動作させる。当然遅くなる。
で、最近出たmatlab 2015bですが、Intel MKLが再び丸め変更が効くようになったという噂があり、3年ぶりにちゃんと精度保証の出来るmatlabになったかと期待されていました。しかし、Rump先生のテストによると結果は残念なものだったそうです。確かにIntel MKLはちゃんと動くようになったそうですが、今度は行列a, bに対する a .* b のような演算で丸め変更が効かなくなってしまったそうです。このような簡単な計算で外部のBLASを呼ぶとは考えにくく、恐らくこれはmatlab内部で完結した処理と考えられます。matlab自身でマルチスレッドでデータを分割して計算するような実装になっていて、そのとき他スレッドに丸めの向きの情報を伝えていないと予想されます。
たまたまうまく行っていた「他人のふんどしで精度保証する」方法論はそろそろ限界なんじゃないでしょうか。自分のコントロールできる範囲内の事柄で精度が保証できている証拠を構成するようにアルゴリズム全体を設計するべきだと思います。
2014/10/01(水)山梨精度保証研究会のスライド
yamanashi.pdf
kvライブラリの簡単な説明、使い方 + jsiam2013のスライドからODEの説明を引用、の構成です。他の資料やホワイトボードも使ったのでこのスライドでしゃべった内容を網羅してるわけではありません。(スライドを作っていて途中で力尽きた、とも言う。)
なお、kvライブラリのガンマ関数の部分(gamma, digamma, trigamma)はまだまだ完成度が低く、現在改良中です。今のバージョンはあまり信用しない方がいいかも。