2014/12/25(木)kv-0.4.16
今回は特に大きなバグが見つかったわけではありません。
- Smithの定理を使ったDKAの精度保証版を作ってみた。
- gamma関数を少し整備した。
- defint-singular.hppの中にひっそりとある端点特異性を持つ関数の積分に、ステップ幅を自動調節するversionを追加した。
某所でLaguerre関数を含む凶悪な(?)数値積分が話題になり、その計算できちんと精度を出すためにいろいろと試行錯誤した結果が反映されています。
この積分を通じて、kvライブラリの欠点が見えてきました。
- この積分は全体を超高精度で行えばちゃんとまともな精度保証結果が出ることは分かっているが、それは現実的に無理。
- 高精度が必要なのは全体のある一部分だが、kvライブラリはworking precisionを全体で一斉に変えることを想定していて、一部分だけ計算精度を変える混合精度計算が書きづらい。
2014/12/16(火)C99のfma関数の挙動を調査
HaswellとFMA
の記事で、Haswellに新しく実装されたFMA命令について書きました。某Mさんがたまたまfmaという命令がmath.hにあるのを見つけてくれてその存在を知ったので、どういうものなのか調査してみました。かなりややこしいのですがせっかくなので記憶が薄れないうちに記録を残しておきます。
まず、fmaという命令はC99で追加されていて、使うときにはmath.hが必要らしいです。そこで、
#include <stdio.h>
#include <math.h>
int main()
{
double u, x, y, z;
int i;
u = 1;
for (i=0; i<52; i++) u /= 2;
x = 1+u;
y = 1-u;
z = -1;
printf("%.15g\n", fma(x, y, z));
}
というプログラムを作って、その挙動を観察してみました。まずコンパイルの可否。次の表のようになりました。
| オプション無し | -lm | -mfma | |
|---|---|---|---|
| gcc4.1 | x | x | x |
| gcc4.4 | x | o | x |
| gcc4.8 | x | o | o |
| IvyBridge | Haswell | |
|---|---|---|
| gcc4.4 -lm | 0 | -4.93038065763132e-32 |
| gcc4.8 -lm | -4.93038065763132e-32 | -4.93038065763132e-32 |
| gcc4.8 -mfma | 実行できず | -4.93038065763132e-32 |
- FMA命令がちゃんと機能していれば、真の値-2-104が、
- FMAでなくただの乗算+加算だと、1-2-104が1に丸められ、それに(-1)を足すので0が、
これらの実験結果を見ると、次のような推定が出来ます。
- gcc4.1では、C99のfma関数のサポートそのものが無い。
- gcc4.4では、C99のfma関数が実装され、libm内にfma関数が存在する。-mfmaによるHaswellのFMA命令の有効化は実装されていない。libm内のfma関数は、CPUがFMA命令を持っていればそれを使い、持っていなければ単にfma(a,b,c)=a*b+cを実行する。
- gcc4.8では、-mfmaによるfma命令の有効化が実装された。これを付けてコンパイルすると、CPUがFMA命令を持つことが前提のコードが生成され、main関数中のfmaはlibm呼び出しではなく直接HaswellのFMA命令にコンパイルされる。
- gcc4.8で更に注目するべきは、libm呼び出しの場合IvyBridgeでも何故か正しい値が計算されたことである。これは普通ではなかなか出来ないはずで、CPUがFMA命令を持たなかった場合は(例えばmpfrを用いた)正確なFMA命令のエミュレーションを行うような実装が行われたと思われる。
| IvyBridge | Haswell | |
|---|---|---|
| gcc4.4 -lm | 2.46 | 2.236 |
| gcc4.8 -lm | 127.42 | 2.828 |
| gcc4.8 -mfma | - | 2.214 |
2014/12/08(月)kv-0.4.15、シンプルな区間演算ライブラリ
今回は、ベキ級数演算の乗算の問題を修正しました。ベキ級数演算では次数を上げながら同じ式を何度も計算する場面が多く、そのときに前回の計算結果を流用すると高速化できるため、計算の履歴を保存しておいて再利用する機構を持っています。ベキ級数の乗算においてこの再利用部分にバグがあり、区間幅が狭くなってしまうことがありました。これは、Type-I PSAの直後にType-II PSAを行った場合のみ稀に発生します。精度保証への影響ですが、常微分方程式ではその計算は候補者集合の大きさを決める目安として使うだけなので恐らく影響なし、数値積分の方は精度保証結果に影響していた可能性があります。
もう一つ、区間演算で、"0.1" < xのように左側に文字列、右側に区間が来るような不等号が正しく計算されないバグも見つかり、修正しました。この計算は自分のライブラリ内では一箇所も使っていませんでしたが、interval.hppを既に何かに利用されている方がいたら、そのプログラムに影響します。
また、久しぶりにVisual Studio 2013でコンパイルしてみたら、新規に書いた部分でいくらかコンパイルが通らない箇所があったので修正しておきました。
「お前のプログラムは本当に精度保証できているのか」と不安になるようなアップデート内容ですが、こうして一つ一つ問題点を修正して完成度を高めていくしかないと信じています。
おまけ: kvライブラリの区間演算の部分を切り出して、簡単な区間演算ライブラリを作ってみました。
interval-simple.tar.gz
- テンプレートを排除しました。従って内部型はdoubleのみですが、プログラムが読みやすくなっています。
- テンプレートを排除したおかげでboostに依存しません。単体で使えます。
- 必要なファイルはinterval.hpp一つです。
- 内部型のカスタマイズが出来ないこと以外は、kvライブラリに含まれるinterval.hppと機能は同等です。数学関数も多数あります。
- 丸めの変更は単純にfesetroundを使っています。
- 文字列との方向丸め付き相互変換機能もあります。従って、文字列からその文字列の表す数値を含むように区間を初期化できるし、表示も真の値を含むように外側に丸めるようになっています。
- volatileを使った最適化対策はきちんとやってます。
2014/12/04(木)tanhとkv-0.4.14
なんだかユーザが不安になりそうなアップデートの頻度で心苦しいのですが、問題が見つかったのだから仕方がないと考えています。だんだん実戦投入される場面が増えてきたおかげと喜んでいます。
今回は、tanh(x)をsinh(x)/cosh(x)と単純に実装していたことによる問題です。この実装だと、|x|が大きい領域ではtanhは-1または1ですがsinhやcoshはとても大きくなりオーバーフローしてしまいます。精度保証的に嘘をつくわけではないですが、オーバーフローで∞/∞がNaNになってしまい、計算が続行不可能になっていました。
x>>0な領域では1-2/(1+exp(2x)), x<<0な領域では2/(1+exp(-2x))-1で計算するように直しました。こんな初歩的なミスをするとは情けない。しかし、ググってみると同じようなミスをしている実装が結構見つかりますね。
ついでに、非線形方程式の全解探索関係の卒論生が何人かいるので、書きかけで完成度は低いですが、全解探索の解説のところにアルゴリズムの解説pdfを追加しておきました。
2014/12/01(月)T先生からの挑戦状続き (多倍長区間演算)
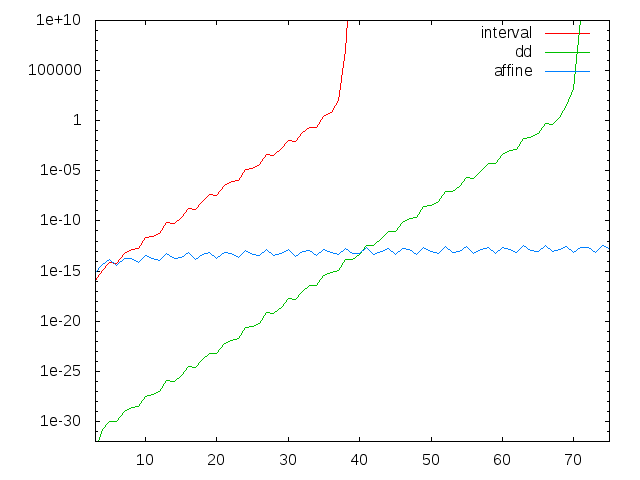
で、ddを使えば一応爆発を「遅らせる」ことは出来るので、超多倍長計算をすれば強引にn=10000まで到達させることは出来るのではないか、と推測できます。
KVライブラリはmpfrラッパーを持っており、mpfrがインストールされた環境下では簡単にmpfrを使えます。mpfrは有名な多倍長浮動小数点演算ライブラリで、最近のgccではコンパイル時に式中の定数の評価にmpfrを使ったりするので、知らないうちにインストールされていることも多いと思います。プログラムはこんな感じ。
#include <kv/interval.hpp>
#include <kv/mpfr.hpp>
#include <kv/rmpfr.hpp>
int main()
{
int i;
kv::interval< kv::mpfr<17000> > x, y, z;
std::cout.precision(17);
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
コンパイル(リンク)時には-lmpfrを付けます。これを実行すると、2 [3,3] 3 [0.77777777777777777,0.77777777777777778] 4 [1.4081632653061224,1.4081632653061225] 5 [2.4744801512287334,2.4744801512287335] (中略) 9997 [1.0388807450632487,1.0388807450632488] 9998 [2.9584219778650379,2.958421977865038] 9999 [0.76071510663969069,0.7607151066396907] 10000 [1.4727965250386843,1.4727965250386844]のように、仮数部17000bitの浮動小数点数を使って、n=10000まで計算出来ました。区間幅のグラフは以下の通り。
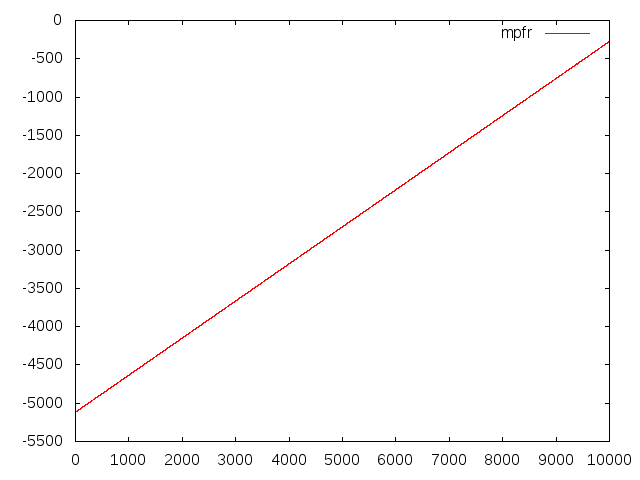
gnuplotがアンダーフローしてしまうので区間幅はlog10を取った値。有効数字10進5000桁もの計算をすれば、何とかn=10000に耐えられることが分かります。計算時間は、以下の通り。
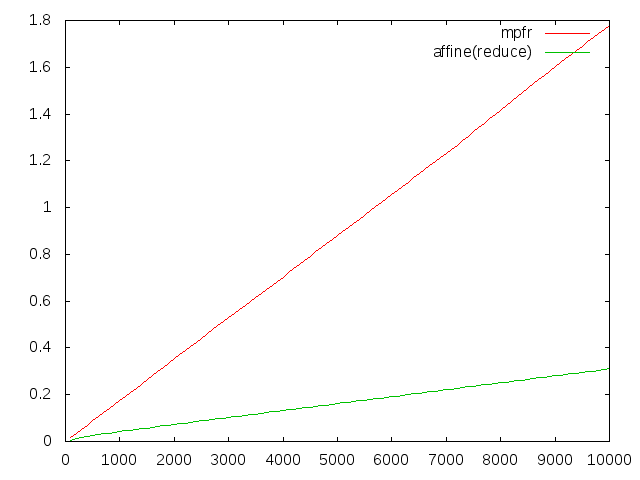
当然ながらnに対して線形。およそ2秒弱と、affine(reduce)には及ばないもののかなり高速です。しかし、例えばn=100000にしようと思うと、より仮数部のbit数が必要になり、計算時間は厳しくなるでしょう。あるいは、初期値にはじめから幅があるような計算をさせようと思うと、高精度計算しても何の意味もなく即死してしまい、affine arithmeticのような手法がどうしても必要になります。
ついでに、Y先生のところのMさんが作成した、LILIBという多倍長区間演算ライブラリを試してみました。こちらは単体で区間演算をサポートするようで、KVライブラリへの組み込みは試していません。LongFloatという多倍長浮動小数点数型に方向付き丸めの機能があれば、組み込みは可能とは思いますが。で、LILIB単体でのQRT写像計算はこちら。仮数部の長さは10進5000桁に設定しています。
#include <iostream>
#include "lilib.h"
int main(){
lilib::setPrecision(5000);
LongInterval x, y, z;
int i;
x = 1.;
y = 1.;
for (i=2; i<=10000; i++) {
z = (1 + 2 * y) / (x * y * y);
std::cout << i << " " << z << "\n";
x = y;
y = z;
}
}
必要ファイルは、lilib.hとライブラリをmakeして出来るlibli.a。コンパイルは、必要ならば両者が見えるように-Iや-Lでサーチパスを設定して、-lliを付ければOK。実行結果は以下の通り。2 < 3.000000, 2.177677e-5009> 3 < 7.777778e-1, 2.177677e-5009> 4 < 1.408163, 1.328045e-5008> 5 < 2.474480, 7.583944e-5008> (中略) 9997 < 1.038881, 3.292724e-167> 9998 < 2.958422, 2.823943e-166> 9999 < 7.607151e-1, 2.314535e-166> 10000 < 1.472797, 1.307194e-165>中心半径型の表記になっていて、中心の表示に大きな丸め誤差が入っていそうなのが気になりますが、ちゃんと計算できているようです。
計算時間は260秒ほどで、残念ながらmpfrには大きく負けてしまいました。今後の発展に期待です。