2016/05/08(日)新しいODE solverの性能評価
x''- μ(1-x2)x'+x = 0この方程式はμ≥0の値によって計算のしやすさが変化し、μが1くらいまでなら計算しやすいnon-stiffな方程式ですが、μが大きくなると極めて計算しづらいstiffな方程式になります。ここでは、μ=1とμ=100でこの方程式の軌道を計算し、ステップ幅の変化を調べてみました。ステップ幅はある方法で局所誤差がmachine epsilon程度になるように計算していますが、stiffなODEの場合そこを変えて大きなステップ幅にしても精度保証の根幹となる不動点定理が成立しなくなってしまい小さなステップ幅への修正を強いられてしまいます。初期値は
x(0) = x'(0) = 1とし、t=200まで計算しました。この軌道を相図(phase diagram)で示すと、次のような感じです。まずμ=1の場合:
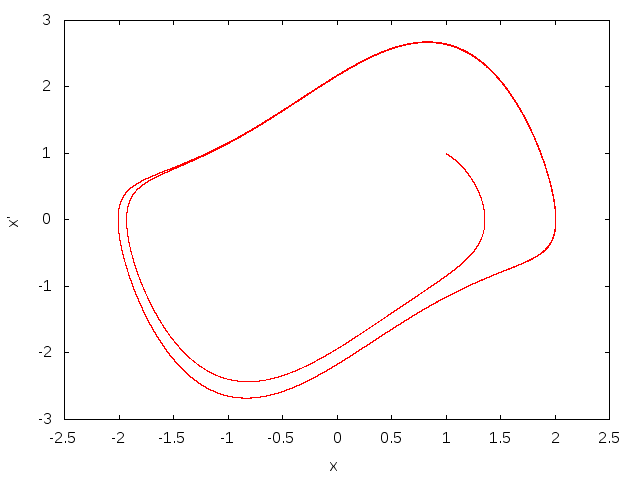
周期解(limit cycle)に巻き付いている様子がよく分かります。次にμ=100の場合:
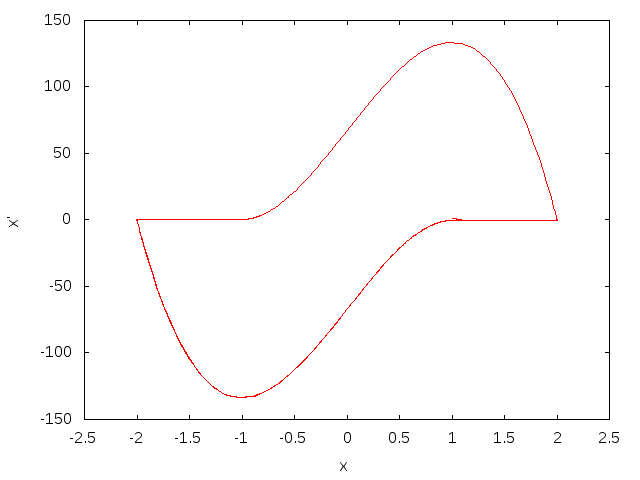
こちらは急激な変化を含んだ周期の長い軌道になります。
さて、これを、
- ode-maffine (従来の標準的なアルゴリズム)
- ode-maffine2 (従来の高速アルゴリズム。初期値に関する微分が出来ない欠点がある)
- ode-maffine3 (新しいアルゴリズム)
- awa (Lohnerによる有名な精度保証プログラム)
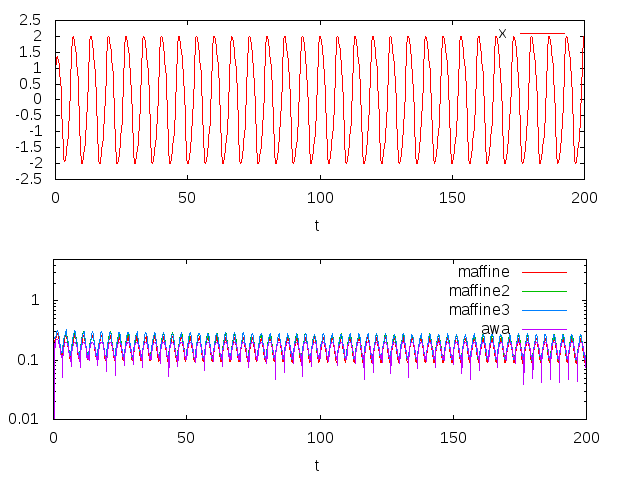
横軸は時刻tで、縦軸は上のグラフがx、下のグラフがODE Solverが選んだステップ幅です。non-stiffな方程式なので、どれでもあまり大きな違いがないことが分かります。計算時間は、
| アルゴリズム | 計算時間(sec) |
|---|---|
| maffine | 2.276 |
| maffine2 | 1.240 |
| maffine3 | 1.798 |
| awa | 3.815 |
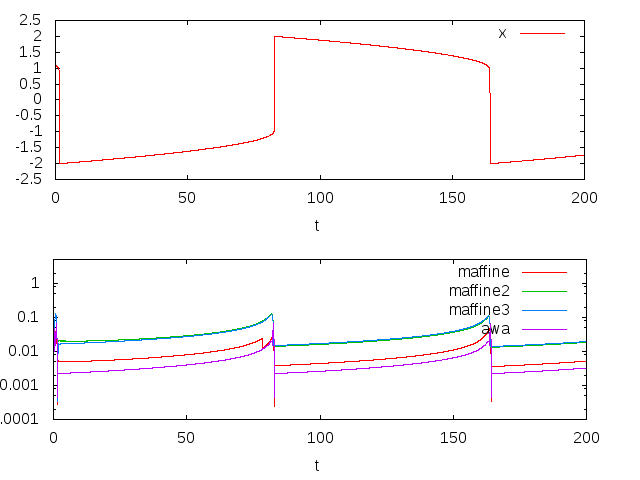
どの方法もμ=1の場合に比べると刻み幅が小さくなっています。変化の激しさに応じて刻み幅を頑張って適応させていることがよく分かります。刻み幅はawaが一番小さく、次にmaffine、maffine2とmaffine3はほぼ同じで比較的大きい刻み幅で計算できていることが分かります。結果として、計算時間にも次のように大きな差が出ました。
| アルゴリズム | 計算時間(sec) |
|---|---|
| maffine | 53.820 |
| maffine2 | 9.287 |
| maffine3 | 13.478 |
| awa | 176.78 |
- maffine → 消滅 (別名で残すかも)
- maffine2 → 従来通り
- maffine3 → maffineに改名