kashiの日記

検索条件

全5件 (1/1ページ) 記事本文を表示

2016/05/21(土)カシオの関数電卓の奇妙な挙動

カシオの関数電卓をいじっていて、とても奇妙な挙動に気づいたので記録を残しておきます。使用したのはfx-5800Pという機種で、内部演算精度は10進数15桁です。結論から書くと、次のような現象を発見しました。

123456789123456 - 123456789121111 = 2345
123456789123456 - 123456789123111 = 345
123456789123456 - 123456789123411 = 0 (45でない!)

非常に近い2つの数同士の引き算を行なうと、「桁落ち」と呼ばれる有効数字の減少が発生します。これは有限精度の計算を行っている以上仕方のないことですが、どうやらこの関数電卓では、

「減算で桁落ちが発生した結果有効数字が2桁以下になったとき、その数を強制的に0に書き換える」

という仕様になっているようです。桁落ちが起きるような厳しい計算こそ高精度な電卓の助けが欲しいところなのに、そこでわざわざかろうじて残った情報を捨て去ってしまうというのは極めて不可解な仕様だと感じます。

この仕様で困ってしまう場面はいくらでもありそうですが、一つ例を作ってみました。2次方程式

0.9999996 x² - 2x + 1.0000004 = 0

の解をいわゆる2次方程式の解の公式で計算してみます。判別式の値は、

4 - 4 × 0.9999996 × 1.0000004
= 4 - 3.99999999999936
= 0.00000000000064
= 6.4 × 10^-13

ですが、この値が

4 - 3.99999999999936 = 0

となってしまいます。3.99999999999936を正しく格納できる仮数部を持っているにも関わらず、です。実にもったいない仕様だとは思いませんか。素直な10進数15桁の演算ならば、

sqrt(6.4 × 10^-13) = 8 × 10^-7
x₁ = (2 - 8×10^-7)/2/0.9999996 = 1
x₂ = (2 + 8×10^-7)/2/0.9999996 ≈ 1.000000800000032

のようにほぼ正確に計算できたはずなのに、

x₁ ≈ 1.00000040000016
x₂ ≈ 1.00000040000016

のような重解になってしまいます。また、手作業で解の公式を使って計算した場合のみならず、関数電卓に組み込まれた2次方程式ソルバーを使っても全く同じ計算結果が得られました。すなわち、ユーザに直接見える部分のみならず、内部の演算ルーチンそのものがこの仕様に蝕まれていることは確実と思われます。

この仕様はカシオfx-5800Pに特有のものなのか、他の機種にも見られるものなのか、ヨドバシカメラの関数電卓売り場の展示機を触って調べてみました。すると、

機種名	仮数部の桁数	桁落ち時に捨てられる桁数
カシオ fx-5800P/JP900/FD10Pro/375ES/72F	15	2
キヤノン F-789SG	18	2
キヤノン F-715SA	16	3
シャープ EL-509M	14	1

のようになりました。試した限りの全ての関数電卓で、桁数の違いこそあれこのような「過桁落ち」処理がなされているようです。全く理解できないのですが、どなたか事情をご存知なら教えて欲しいものです。

コメント（6件）

2016/05/09(月)kv-0.4.36

精度保証

というわけで、予告通りkvライブラリを0.4.36にアップデートしました。

内容は前回の記事の予告通りで、maffine3を正式アルゴリズムに昇格させました。

maffine → 一応maffine0として残したが消滅候補
maffine2 → そのまま
maffine3 → maffineに改名

使い勝手は0.4.34以前と変わらず、単に性能がよくなっているはずです。

コメント（0件）

2016/05/08(日)新しいODE solverの性能評価

精度保証

さて、前回の記事で書いた新しいアルゴリズムの性能を簡単な例で示します。例として選んだのはvan der Pol方程式です。

x''- μ(1-x²)x'+x = 0

この方程式はμ≥0の値によって計算のしやすさが変化し、μが1くらいまでなら計算しやすいnon-stiffな方程式ですが、μが大きくなると極めて計算しづらいstiffな方程式になります。ここでは、μ=1とμ=100でこの方程式の軌道を計算し、ステップ幅の変化を調べてみました。ステップ幅はある方法で局所誤差がmachine epsilon程度になるように計算していますが、stiffなODEの場合そこを変えて大きなステップ幅にしても精度保証の根幹となる不動点定理が成立しなくなってしまい小さなステップ幅への修正を強いられてしまいます。初期値は

x(0) = x'(0) = 1

とし、t=200まで計算しました。この軌道を相図(phase diagram)で示すと、次のような感じです。まずμ=1の場合:

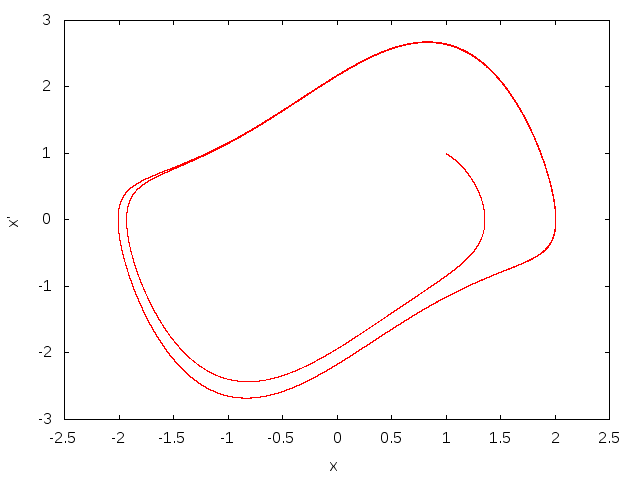
周期解(limit cycle)に巻き付いている様子がよく分かります。次にμ=100の場合:

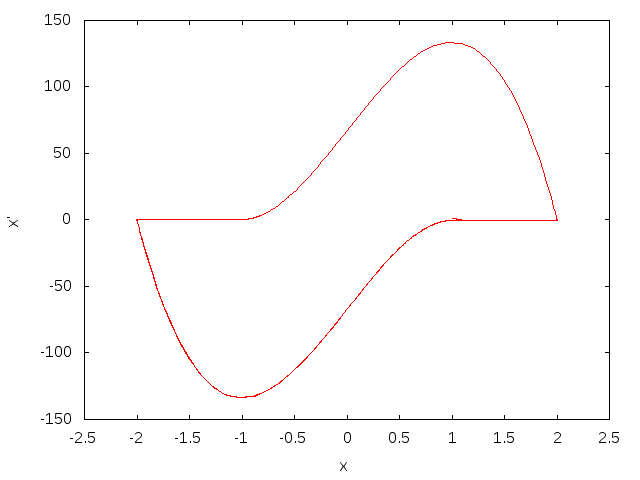
こちらは急激な変化を含んだ周期の長い軌道になります。

さて、これを、

ode-maffine (従来の標準的なアルゴリズム)
ode-maffine2 (従来の高速アルゴリズム。初期値に関する微分が出来ない欠点がある)
ode-maffine3 (新しいアルゴリズム)
awa (Lohnerによる有名な精度保証プログラム)

で計算して比較してみます。まずμ=1で:

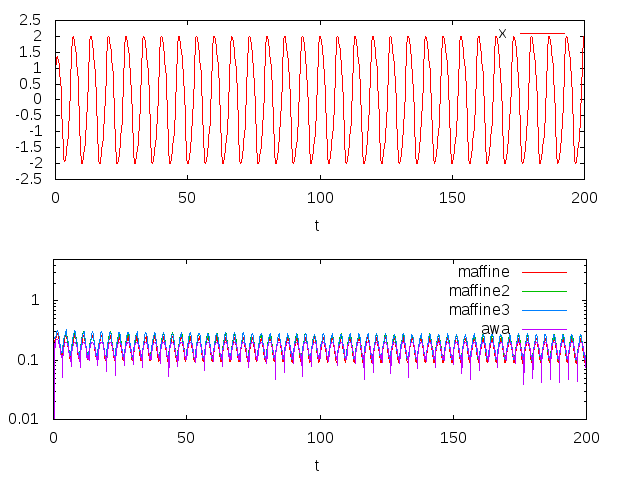
横軸は時刻tで、縦軸は上のグラフがx、下のグラフがODE Solverが選んだステップ幅です。non-stiffな方程式なので、どれでもあまり大きな違いがないことが分かります。計算時間は、

アルゴリズム	計算時間(sec)
maffine	2.276
maffine2	1.240
maffine3	1.798
awa	3.815

でした。次に、μ=100の場合を示します。

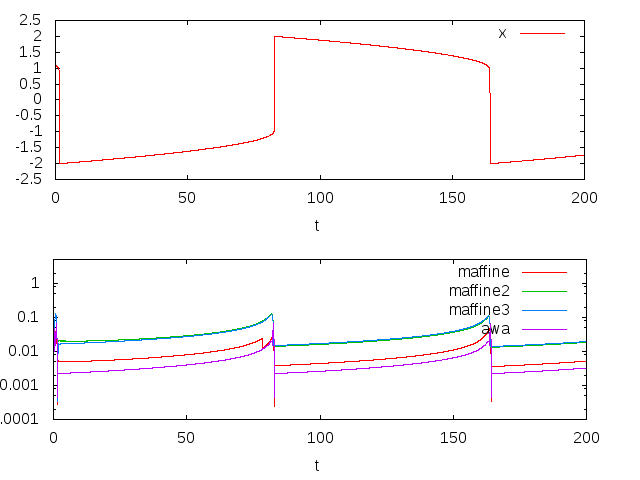
どの方法もμ=1の場合に比べると刻み幅が小さくなっています。変化の激しさに応じて刻み幅を頑張って適応させていることがよく分かります。刻み幅はawaが一番小さく、次にmaffine、maffine2とmaffine3はほぼ同じで比較的大きい刻み幅で計算できていることが分かります。結果として、計算時間にも次のように大きな差が出ました。

アルゴリズム	計算時間(sec)
maffine	53.820
maffine2	9.287
maffine3	13.478
awa	176.78

maffine3はmaffineと完全に同じことが出来て性能が良さそうなので、maffineを残す意味はなさそうです。次期versionでは、

maffine → 消滅 (別名で残すかも)
maffine2 → 従来通り
maffine3 → maffineに改名

としたいと思います。これなら0.4.34以前と使い勝手は変わらずに単に性能が良くなったということになります。関数名の変更はユーザに混乱をもたらすので、現version (0.4.35) はなるべく短命にするつもりです。

コメント（0件）

2016/05/06(金)kv-0.4.35

精度保証

kvライブラリを0.4.35にアップデートしました。

まず、前回(0.4.34)に混ぜてしまったバグの修正です。1.00e-05みたいな数値が1.00e0-5のように表示されてしまうというバグを直しました。

また、常微分方程式のsolverに新しいアルゴリズム(maffine3)を追加しました。kv-0.4.30とstiffなODEで日記に書いたように、maffineはstiffなODEに弱く、maffine2はstiffに強いが初期値に関する精度保証された微分が得られないという状況でしたが、今回、「stiffに強くて初期値に関する微分もできる」maffine3を追加しました。今年のGWはほぼこの実装に費やしてしまいました。

実装したアルゴリズムのアイデアは極めて単純です。常微分方程式の初期値問題を精度よく解くためには、いわゆるWrapping Effectを防ぐために解の初期値に関する微分を利用することがほぼ必須です。それを計算するのに必要なのが「初期値に関する変分方程式」というものです。すなわち、

x'(t)= f(x(t),t)
x(t₀) = x₀

に対して、x^*(t)をこの式の真の解としたy(t)に関する行列微分方程式

y'(t) = f_x(x^*(t), t)y(t)
y(t₀) = I (単位行列)

を初期値に関する変分方程式といいます。ある時刻t₁におけるyの値y(t₁)は、x(t₀)にx(t₁)を対応させる写像のヤコビ行列と一致します。

このyを計算するのに、従来は上の2つの式を連立させて、

x'(t)= f(x(t),t)
y'(t) = f_x(x(t), t)y(t)
x(t₀) = x₀
y(t₀) = I (単位行列)

のようなxとyの組を未知関数とするn+n×n次元の新しい初期値問題を作成し、これを解くという方法を使っていました。その方が実装が楽だったという事情もあります。

それを変更して、まずxだけの式を解いて真の解x^*を区間関数として求め、それを代入してyの式を解く、素直な2段階法が、新しいアルゴリズムです。stiffでない普通の方程式だとどちらを使っても大差ありませんが、stiffな場合だと後者の方が刻み幅が大きくなり、結果として高速になるようです。

アルゴリズムの詳細や性能評価はまた改めて書く予定です。問題が無ければ、将来のバージョンではこの新しいmaffine3をmaffineとし、旧maffineは抹消してしまうことも考えています。

コメント（0件）

2016/05/01(日)emscriptenで遊んでみた

その他

emscriptenという、c/c++のコードをLLVMのバイトコードを経由してjavascriptに変換するコンバータがよく話題になっています。以前、kvライブラリをemscriptenで変換して動かしたというメールを頂いたことがあって、ずっと気になっていました。そこで、ちょっとインストールして遊んでみました。

インストールしたばかりのubuntu 16.04で試しました。しかし、

sudo apt install emscripten

で入れてもうまく動かない模様です。clang/llvmのバージョンの問題っぽいがよく分かりません。

そこで、本家の Download and install — Emscripten 1.36.1 documentation に従ってインストールしてみました。そこではポータブル版というroot権限なしで入れる方法が紹介されていました。その方が周辺ツールのバージョンに左右されなくてインストールが楽なのかな。

sudo apt install cmake

Portable Emscripten SDK for Linux and OS X (emsdk-portable.tar.gz) をダウンロードして展開し、その中にcdして

./emsdk update
./emsdk install latest
./emsdk activate latest

します。最後の作業で/home/kashi/.emscriptenが作られました。これでインストールは終了。使う前に

source emsdk_env.sh

でPATHの設定が必要です。

適当なc++のプログラムを作って、

emcc test.cc
node a.out.js

で動くのを確認しました。

次に、kvのプログラムを動かしてみました。問題はboostで、emscriptenでは外部ライブラリを使ったプログラムはそのままでは動きません。外部ライブラリもソースから変換する必要があります。kvの場合は幸いなことにboostはheader onlyの範囲でしか使っていませんので、大丈夫なはずです。自分は、

ln -s /usr/include/boost ホームのどこか

とリンクを張ってしまって、-Iにそれを指定してごまかしました。これが正しいかどうかは分かりません。また、javascriptの中ではfesetroundによる丸めの向きの変更は効かないので、そのままでは精度保証出来ません。kvは-DKV_NOHWROUNDを付けると丸めの向きの変更を行わずエミュレーションで方向付き丸めを行なう機能を持っており、それをつけるとちゃんと精度保証付きで計算してくれるようです。

emcc -I(kvの場所) -I(boostの場所) -DKV_NOHWROUND hoge.cc

みたいな感じです。kvのサンプルはmpfrを使ったもの以外は大体動きそうです。実行速度はちゃんと測ってませんがネイティブのC++の30倍程度でしょうか。htmlに変換してfirefoxに食わせた方がnode.jsより速いようにも見えました。

単なる遊びであってあまり意味はないですが、楽しいです。

コメント（0件）