2016/10/02(日)scan2016
自分が発表した内容は大体5月に この記事 に書いたもので、だいぶ忘れかけていたので何というか気合いがなかなか入らなくて大変でした。行きの飛行機の中で電源が使えたのが大助かり。stiffなODEをどう効率的に精度保証するか、というのは何年も前からこの業界の大きなテーマで、それなりに印象を残せたのではないかと勝手に考えています。
この業界は狭くて研究者の数が多くないので、朝から晩までずっと精度保証の話を聞くという機会は滅多に無く、どの話も刺激的で大変満足出来ました。(こういう機会に自分の発表だけしてさっさと遊びに行っちゃう人は何を考えてるんだろう、と毒を吐いておこう。誰が何をしようと勝手だけど、そういう人とは友達になれないなあ。)
メキシコから来た某juliaおじさんのjulia押しが強力で割と印象に残りました。C++のテンプレートのような、型に合わせて何通りもの新しい関数を自動生成する機能があるようで、うまく使えば確かに精度保証付き数値計算にフィットするかなと。
また、double-doubleの誤差評価を厳密に頑張る話もなかなか楽しそう。某Y氏が数年前にやろうとしてた気がするが、それとの関係はどうなんだろうか。
Csendesの話面白かった。やはり遅延微分方程式に手を出すべきか?
Tuckerがオーガナイザーだったせいか、ODEの話が多めでしたね。国府先生の話で出てきた宮路先生のTaylorモデルの実装とか、興味あるなあ。
2年後に東京で開催することが正式に決定したので、頑張らないと!

















2016/08/03(水)半精度浮動小数点数に関する思考実験
IEEE754-2008の半精度では、16bitを符号s(1bit)+指数部e(5bit)+仮数部m(10bit)に分割しています。指数部のオフセットは15で、従って正規化数は
x = (-1)s × 1.m × 2e-15のように、非正規化数は
x = (-1)s × 0.m × 2-14のように実数xと対応します。
ところで、URRという浮動小数点数の表現形式をご存知でしょうか。浜田穂積先生が80年代(IEEE754制定より前!)に提案された浮動小数点数の表現形式です。詳細は
- 浜田 穂積, 二重指数分割に基づくデータ長独立実数値表現法, 情報処理学会論文誌, Vol.22, No. 6, pp. 521-526 (1981)
- 浜田 穂積, 二重指数分割に基づくデータ長独立実数値表現法II, 情報処理学会論文誌, Vol.24, No. 2, pp. 149-156 (1983)
さて、半精度浮動小数点数は、bit数が少ないこともあって表現できる数値の範囲が非常に狭く、簡単にアンダーフローやオーバーフローを起こしてしまいます。正の最大数は何と65504です。正の最小数は、精度を保っている正規化数で2-14≃6.1×10-5、非正規化数まで考えても2-24≃5.96×10-8にすぎません。
そこで、URR的な考え方を用いて16bit浮動小数点数を構成したらどうなるか考えてみました。URRは-infやNaNが無いなど、現代のIEEE754に慣れた我々には使いにくいところもあるので、指数部と仮数部の区切りを可変にするという思想はそのままで、適当にフォーマットを定めます。指数部は、Eliasのデルタ符号を用いることにします。デルタ符号は1,2,3,…の自然数しか表せないので、指数部とデルタ符号で表す数値を
| デルタ符号 | 1 | 2 | 3 | 4 | 5 | … | 255 | 256 | … | 508 | 509 | 510 | 511 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 指数部 | 0 | -1 | 1 | -2 | 2 | … | 127 | -128 | … | -254 | ±0 | ±inf | NaN |
| デルタ符号の長さ | 1 | 3 | 3 | 5 | 5 | … | 14 | 15 | … | 15 | 15 | 15 | 15 |
| 提案方式の仮数部長 | IEEE754-2008の仮数部長 | |
|---|---|---|
| 2-254 | 1 | - |
| ⋮ | ⋮ | ⋮ |
| 2-128 | 1 | - |
| 2-127 | 2 | - |
| ⋮ | ⋮ | ⋮ |
| 2-24 | 6 | 1 |
| 2-23 | 6 | 2 |
| 2-22 | 6 | 3 |
| ⋮ | ⋮ | ⋮ |
| 2-16 | 6 | 9 |
| 2-15 | 7 | 10 |
| 2-14 | 7 | 11 |
| ⋮ | ⋮ | ⋮ |
| 2-8 | 7 | 11 |
| 2-7 | 8 | 11 |
| ⋮ | ⋮ | ⋮ |
| 2-4 | 8 | 11 |
| 2-3 | 11 | 11 |
| 2-2 | 11 | 11 |
| 2-1 | 13 | 11 |
| 20 | 15 | 11 |
| 21 | 13 | 11 |
| 22 | 11 | 11 |
| 23 | 11 | 11 |
| 24 | 8 | 11 |
| ⋮ | ⋮ | ⋮ |
| 27 | 8 | 11 |
| 28 | 7 | 11 |
| ⋮ | ⋮ | ⋮ |
| 214 | 7 | 11 |
| 215 | 7 | 11 |
| 216 | 6 | - |
| ⋮ | ⋮ | ⋮ |
| 2127 | 2 | - |
| 2128 | 1 | - |
| ⋮ | ⋮ | ⋮ |
| 2253 | 1 | - |
もちろんハードウェアのサポートが無くソフトウェアエミュレーションでは速度は絶望的ですが、将来このような優れたフォーマットが気軽に使えるようになればいいなと思っています。FPGAとかで作って遊んだりできないかなあ。
2016/06/20(月)方向付き丸めクイズ
- x = a + b
- x = a - b
- x = a × b
- x = a / b
- x = (a + b) + c
- x = (a × b) × c
- x = (a - b) - c
- x = a - (b + c)
- x = -a + b
- x = -( (-a) + (-b) )
- x = a × b + c × d
- x = (a + b) × (c + d)
- x = a / (b + c)
- x = a - b × c
- x = a + (-b) × c
- x = sqrt(a)
- x = exp(a)
2016/05/09(月)kv-0.4.36
内容は前回の記事の予告通りで、maffine3を正式アルゴリズムに昇格させました。
- maffine → 一応maffine0として残したが消滅候補
- maffine2 → そのまま
- maffine3 → maffineに改名
2016/05/08(日)新しいODE solverの性能評価
x''- μ(1-x2)x'+x = 0この方程式はμ≥0の値によって計算のしやすさが変化し、μが1くらいまでなら計算しやすいnon-stiffな方程式ですが、μが大きくなると極めて計算しづらいstiffな方程式になります。ここでは、μ=1とμ=100でこの方程式の軌道を計算し、ステップ幅の変化を調べてみました。ステップ幅はある方法で局所誤差がmachine epsilon程度になるように計算していますが、stiffなODEの場合そこを変えて大きなステップ幅にしても精度保証の根幹となる不動点定理が成立しなくなってしまい小さなステップ幅への修正を強いられてしまいます。初期値は
x(0) = x'(0) = 1とし、t=200まで計算しました。この軌道を相図(phase diagram)で示すと、次のような感じです。まずμ=1の場合:
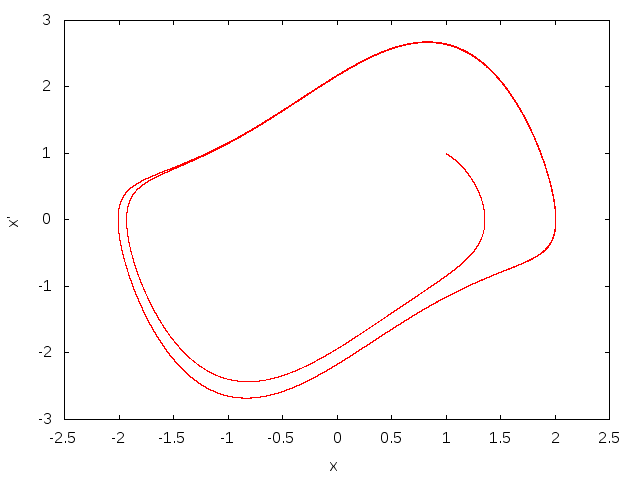
周期解(limit cycle)に巻き付いている様子がよく分かります。次にμ=100の場合:
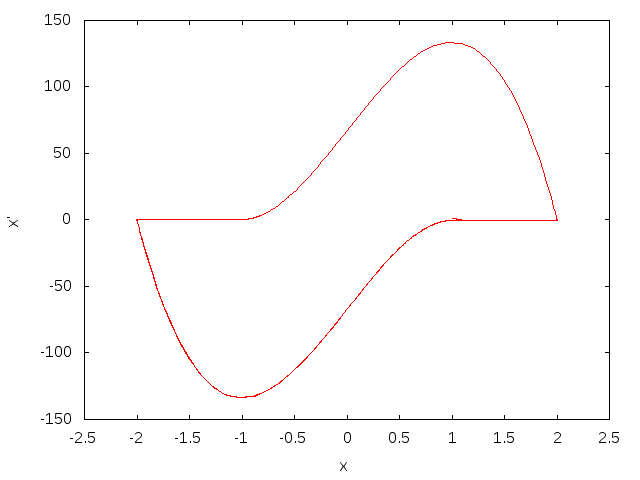
こちらは急激な変化を含んだ周期の長い軌道になります。
さて、これを、
- ode-maffine (従来の標準的なアルゴリズム)
- ode-maffine2 (従来の高速アルゴリズム。初期値に関する微分が出来ない欠点がある)
- ode-maffine3 (新しいアルゴリズム)
- awa (Lohnerによる有名な精度保証プログラム)
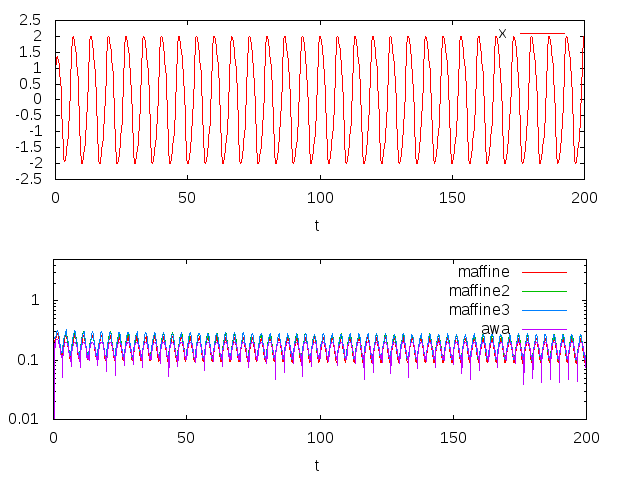
横軸は時刻tで、縦軸は上のグラフがx、下のグラフがODE Solverが選んだステップ幅です。non-stiffな方程式なので、どれでもあまり大きな違いがないことが分かります。計算時間は、
| アルゴリズム | 計算時間(sec) |
|---|---|
| maffine | 2.276 |
| maffine2 | 1.240 |
| maffine3 | 1.798 |
| awa | 3.815 |
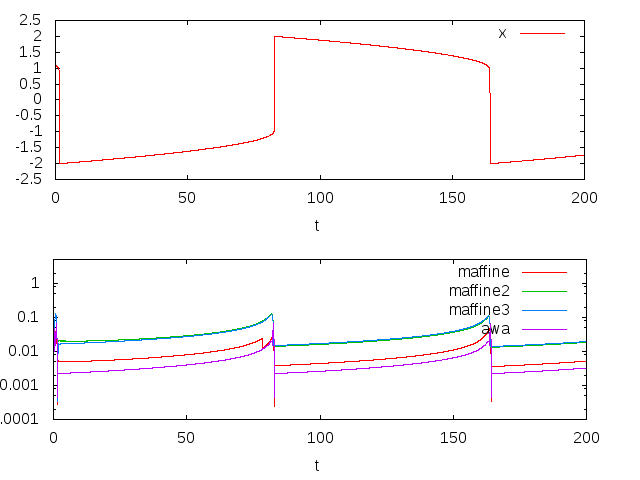
どの方法もμ=1の場合に比べると刻み幅が小さくなっています。変化の激しさに応じて刻み幅を頑張って適応させていることがよく分かります。刻み幅はawaが一番小さく、次にmaffine、maffine2とmaffine3はほぼ同じで比較的大きい刻み幅で計算できていることが分かります。結果として、計算時間にも次のように大きな差が出ました。
| アルゴリズム | 計算時間(sec) |
|---|---|
| maffine | 53.820 |
| maffine2 | 9.287 |
| maffine3 | 13.478 |
| awa | 176.78 |
- maffine → 消滅 (別名で残すかも)
- maffine2 → 従来通り
- maffine3 → maffineに改名